Синтез сети абонентского доступа

Построение моделей телекоммуникационной сети.

1.1. Исходные данные, согласно варианту 01, приведены в таб. 1. 1 в которой первая и вторая строка содержат номера пунктов, соединенных линиями связи, а в третей строке содержатся весовые характеристики этих линий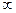

Н.В.

К.В.

Вес

Таблица 1.1 – Исходные данные.

Исходная телекоммуникационная сеть содержит 10 пунктов и 19 линий, которые обеспечивают связь между пунктами в обоих направлениях.

1.2.Построить все формы модельного представления исходной телекоммуникационной сети и привести их, снабдив соответствующими комментариями.

А) Графовая модель.

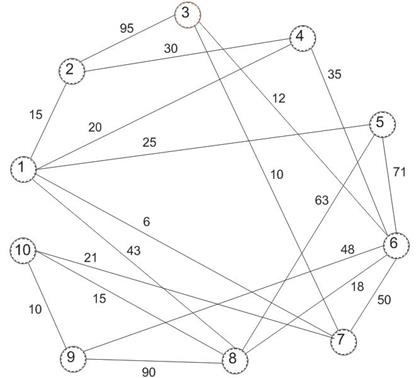Рисунок 1.1 – Графовая модель представления телекоммуникационной сети.

б) Матрица смежности.

Один из наиболее распространенных дискретных представлений графа является матрица смежности. Эта матрица А=[а_i,j], размером (n x n) элементов, которые могут принимать значения: а_i,j = 1, если в графе существует дуга между вершинами i и j; а_i,j = 0, в противном случаи.

Таблица 1.2 – Матрица смежности.

В) Матрица инцидентности.

Матрица инцидентности – это матрица отображающая отношение инцидентности ребер и вершин графа. Между вершинами и соединенными с ней дугами существует инцидентность. Эта матрица B_i,j могут принимать значения (0,1).

1 – 2
1 – 4
1 – 5
1 – 7
1 – 8
2 – 3
2 – 4
3 – 6
3 – 7
4 – 6
5 – 6
5 – 8
6 – 7
6 – 8
6 – 9
7 – 10
8 – 9
8 – 10
9 – 10

Таблица 1.3 – Матрица инцидентности

Г) Матрица весов.

Взвешенный граф (сеть) может в дискретном виде быть представлен матрицей весов W = [W_i,j], где W_i,j – вес дуги(ребра) если она существует в графе. Веса несуществующих дуг (ребер) понимают равными бесконечности или 0 в зависимости от условий задачи, в которой они рассматриваются.

	∞		∞			∞			∞	∞
		∞			∞	∞	∞	∞	∞	∞
	∞		∞	∞	∞			∞	∞	∞
			∞	∞	∞		∞	∞	∞	∞
		∞	∞	∞	∞		∞		∞	∞
	∞	∞				∞				∞
		∞		∞	∞		∞	∞	∞
		∞	∞	∞			∞	∞
	∞	∞	∞	∞	∞		∞		∞
	∞	∞	∞	∞	∞	∞				∞

Таблица 1.4 – Матрица весов.

г) Список дуг (ребер)

Если граф является разрешенным(имеет малое количество дуг(ребер)), то возможность более компактно представление графа. Этот список может быть реализован двумя одномерными массивами размерностью m, в первом из которых записаны начальные вершины дуг(ребер), а во второй – конечные:

R₁ = (1,1,1,1,1,2,2,3,3,4,5,5,6,6,6,7,8,8,9)

R₂ = (2,4,5,7,8,3,4,6,7,6,6,8,7,9,10,9,10,10)

Е) Структура смежностей.

При организации представления графа в виде дискретного массива с плавающими границами, т.е. в случае, когда необходимо предусмотреть возможность добавления или изменения вершины графа, целесообразно использовать структуру смежностей. Последняя представляет собой список смежностей вершины графа. Структура смежностей имеет вид:

1: 2,4,5,7,8 5: 1,6,8 9: 6,8,10

2: 1,3,4 6: 3,4,5,7,8,9 10: 7,8,9

3: 2,6,7 7: 1,3,6,10

4: 1,2,6 8: 1,5,6,9,10

Дать письменный ответ на следующие ключевые вопросы:

1. Какие задачи принадлежат к классу задач синтеза, и какие – к классу анализа?

2. Для чего используют модельное представление сети?

3. Перечислить формы модельного представления телекоммуникационной сети, как объекта синтеза и анализа. Охарактеризовать каждую из них

4. Что называют графом? Ориентированным графом? Не ориентированным графом?

5. В чем состоит отличительная особенность сетевой модели?

Ответы:

1. Задача синтеза состоит в виде оптимальной топологии сети, оптимального количества и места расположения узлов коммутации.

Задача анализа состоит в нахождении оптимальных путей передачи информации, определение совокупности путей заданной транзитивности, оценки пропускной способностью сети, вероятность установления соединения между узлами и т.д. Также к задаче анализа относится расчет характеристики параметров сети в целом, а также отдельных ее элементов (пропускной способности, качества обслуживания и т.п.).

2. Модельное представление сети используется для того, чтобы выявлять и обнаруживать наиболее существенные элементы и связи между ними, не отвлекаясь от деталей. Основное представление – граф.

3. В качестве математической модели телекоммуникационной сети используется граф. Граф может изображаться в геометрическом (точки соединения ребрами) и дискретном (матрицы) видах.

4. Графом называется некоторая совокупность точек и связывающих ребер. Граф в котором задается направление дуг, называется ориентированным. В противном случаи – неориентированным.

5. Отношение смежности отражает вершины соединенные между собой ребром. Отношение инцидентности отражает связь между вершиной и соединенным с ней ребром.

6. Отличительной чертой сетевой модели является то, что каждой дуге (ребру) графа поставлено в соответствие некоторое числовое значение, называемое весом. Такой граф называется взвешенным. При необходимости веса могут быть приписаны также вершинам графа. Весовые характеристики могут выступать расстояния, пропускная способность, стоимость и т.д.

Синтез сети абонентского доступа.

2.1Постройте кабельную сеть абонентского доступа, для которой обеспечивается минимум затрат на линейные сооружения.

Дано:Перечень пунктов сети (n=10) и матрица расстояний между ними. В качестве матрицы расстояний воспользуйтесь матрицей весов, полученной при выполнении задания 1, рассматривая все ребра в качестве расстояния в километрах. Отсутствующие значения элементов матрицы весов следует рассматривать как бесконечно большие расстояния, т.е. невозможность физической прокладки кабеля между некоторыми парами пунктов.

Стоимость 1км. Линейных сооружений на всех направлениях одинакова и равняется 10у.е.

Для решения поставленной задачи используется алгоритм Прима.

Шаг 0: Искомая сеть G^’(N,V^’) в исходном состоянии содержит n = 10 вершине и не содержит ребер. Выбираем одну произвольную вершину (вершина 5) и обозначаем ее как «выбранная». Остальные 9 вершин обозначим как «невыбранные».

Выбранная вершина Невыбранные вершины

5 1,2,3,4,6,7,8,9,10

Шаг 1: Отыскиваем ребро (i,j) принадлежащее графу G(N,V), с минимальным весом, у которого вершина i принадлежит подмножеству «выбранных» вершин, вершина j – подмножество «невыбранных» вершин.

Выбираем ребро (l_5,1) как ребро с наименьшим весом.

l_5,1 = вес 25

Шаг 2:Ребро (i,j) включает в искомую сеть G^’(N,V’), а вершина j исключается из подмножества «невыбранных» вершин и включается в подмножество «выбранных» вершин.

Ребро (l_5,1) вводится в искомый граф G^’(N,V’), а вершина 1 включается подмножество «выбранных» вершин.

l_5,1 = вес 25

Выбранная вершина Невыбранные вершины

5,1 2,3,4,6,7,8,9,10

Шаг 1 и 2 повторяется пока подмножество «невыбранных» вершин не окажется пустым.

l_1,7 – вес 6

Выбранная вершина Невыбранные вершины

5,1,7 2,3,4,6,8,9,10

l_7,3 – вес 10

Выбранная вершина Невыбранные вершины

5,1,7,3 2,4,6,8,9,10

l_3,6 – вес 12

Выбранная вершина Невыбранные вершины

5,1,7,3,6 2,4,8,9,10

l _1,2 – вес 15

Выбранная вершина Невыбранные вершины

5,1,7,3,6,2 4,8,9,10

l _6,8 – вес 18

Выбранная вершина Невыбранные вершины

5,1,7,3,6,2,8 4,9,10

l _8,10 – вес 15

Выбранная вершина Невыбранные вершины

5,1,7,3,6,2,8,10 4,9

l_9,10 – вес 10

Выбранная вершина Невыбранные вершины

5,1,7,3,6,2,8,10,9 4

l_1,4 – вес 20

Выбранная вершина Невыбранные вершины

5,1,7,3,6,2,8,10,9,4 0

На этом работа алгоритма заканчивается, т.к. все вершины оказались помеченными как «выбранные». Полученный искомый граф представляющий собой покрывающее дерево(рис 2,1) т.к. он включает все вершины, содержит число ребер на единицу меньше числа вершины и обеспечивает связность каждой пары вершин.

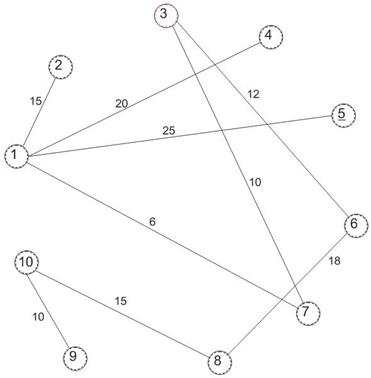Рисунок 2.1 – Искомый граф представляющий собой покрывающее дерево.

Общая стоимость линейных сооружений составляет

S = 10*l = 10(15+20+25+6+12+10+18+15+10) = 1310 y.e.

2.2На синтезированной сети, для которой обеспечивается минимум стоимости линейных сооружений, определите пункт, в котором целесообразно размести опорный узел (ОУ) сети абонентского доступа из соображений минимизации суммарной протяженности абонентских линий от ОУ ко всем абонентским пунктам (АП).

Решением поставленной задачи является определением медианы графа G(N,V),

Вершина m, которая принадлежит N, является медианой графа G(N,V), если она удовлетворяет условию:

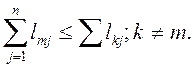
Величина 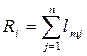называется медианой длиной графа G и представляет наименьшую суммарную длину ребра, которая соединяет вершину m с другими вершинами графа.

Алгоритм определение медианы графа G(N,V), включает такие шаги:

Шаг 1.В исходной матрице весов L = [l_ij], соответствующими длинами ребер, найти сумму элементов каждого ребра:

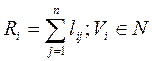
Шаг 2.Среди множества значений (R_i) найти минимальное R_m. Вершина m и будет являтся медианой графа.

Для определения медиана графа построим матрицу расстояний по графу кабельной сети абонентского доступа (рис 2.1) с обеспечением минимума затрат на линейные сооружения

Матрица расстояний по соединительным путями между всеми пунктами сети приведена в таблице 2.1.

											∑
	▬
		▬
			▬
				▬
					▬
						▬
							▬
								▬
									▬
										▬

Таблица 2.1 – Матрица расстояний.

Среди множеств значений сумм элементов каждого ряда находим минимальное R_m = 276.

Вершина m = 7 является медианой графа G.

2.3Для организации абонентской сети со стационарным радио доступом обеспечить выбор места расположения базовой станции (БС), которая обеспечивала бы устойчивую радиосвязь при сравнительно небольшой мощности радиопередатчика.

Дано: перечень пунктов (n = 10) и матрица расстояний. В качестве последней воспользуйтесь матрицей весов, полученной при выполнении задания 1. Отсутствующие значения элементов матрицы следует рассматривать как отсутствие прямой радио видимости между ними.

Решение данной задачи является определение центр графа.

Пускай G(N,V) это граф, где N – множество вершин, а V множество расстояний между всеми вершинами. Вершина S называется центром графа G(N,V), если она удовлетворяет условию

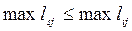_, для любой i;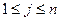

Алгоритм определения центра графа (вершины S) следует из самого определения:

Шаг 1. В каждом ряду исходной матрицы весов L = [l_ij] – отыскиваем элемент с максимальным значением.

R_1max = 83 = l_1,4; R_6max = 33 = l_6,5;

R_2max = 19 = l_2,3; R_7max = 41 = l_7,1;

R_3max = 25 = l_3,7; R_8max = 53 = l_8,9;

R_4max = 83 = l_4,1; R_9max = 53 = l_9,8;

R_5max = 33 = l_5,6; R_10max = 13 = l_10,7;

Шаг 2.Среди множеств максимальных значений элементов рядов определим наименьшее 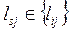. Вершина S₁₀ для которой R_10max = 13 = l_10,7 является центром графа и таким образом является оптимальным месторасположением БС т.к. минимизировав расстояния до самих отдельных вершин графа мы гарантировано обеспечим меньшие расстояния ко всем остальным вершинам графа.

2.4Дать письменный ответ на следующие ключевые вопросы:

1. Для чего предназначена сеть абонентского доступа?

2. Перечислить требования, которым должно удовлетворять решение задачи синтеза сети минимальной стоимости.

3. Какой граф называется деревом, покрывным деревом?

4. Сформируйте идею алгоритма Прима, которая обеспечивает построение сети минимальной стоимости.

5. Можно ли применить алгоритм Прима для построения максимальной стоимости? Если так, то каким образом?

6. Возможно, ли использовать алгоритм Прима при неполносвязной исходной матрицы расстояний? Что это означает?

7. Алгоритм Прима является точным или эвристическим?

8. Какая вершина называется медианой графа? Что является исходными данными для ее определения?

9. Сформировать алгоритм определения медианы графа по матрице расстояния между всеми парами вершины графа.

10. Какая вершина называется центром графа?

11. Сформировать алгоритм определения центра графа.

Ответы:

1. Сети абонентского доступа предназначены для ситуации, в которой определенное множество точек необходимо соединить так, чтобы каждая пара точек соединена непосредственно или через другие точки.

2. Для решения задачи синтеза сети минимальной стоимости требуется, чтобы определенное множество точек было соединены так, чтобы каждая пара точек стала соединенной (непосредственно или через другие точки), а суммарная весовая характеристика связей получалась минимальной.

3. Связный граф (сеть, которая объединяет) называется деревом, если в нем отсутствуют цикли (повторения). Дерево в котором включены все вершины, называется покрывным.

4. Алгоритм Прима реализуется путем установления пометок вершинам, которые вводятся в искомый граф, и последовательно введения у него наиболее коротких ребер, суммарное количество которых не должна превышать (n - 1) и при этом обеспечивать связность между всеми n вершинами покрывного графа.

5. Алгоритм Прима можно использовать для построения максимальной стоимости. Алгоритм реализуется как и в случаи построения сети минимальной стоимости, только последовательно вводится у него наиболее длинные ребра.

6. При неполносвязной исходной матрицы расстояния алгоритм Прима использовать нельзя, так как в результате не получится покрывающее дерево (т.е. не будет обеспечена связность каждой пары вершины).

7. Алгоритм Прима является тончим.

8. Вершина m, которая принадлежит N, является медианой графа G(N,V), если она удовлетворяет условию

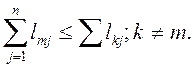
9. Величина 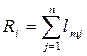называется медианой длиной графа G и представляет наименьшую суммарную длину ребра, которая соединяет вершину m с другими вершинами графа.

10. Вершина S называется центром графа G(N,V), если она удовлетворяет условию 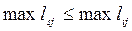_, для любой i; .

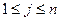11. Алгоритм определения центра графа (вершины S) такой:

1. В каждой строке искомой матрицы весов L = [l_ij] – отыскиваем элемент с максимальным значением.

2.Среди множеств максимальных значений элементов строки отыскиваем наименьшее 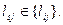Эта вершина и будет являться центром графа.