Шаг 2: Равномерное преобразование гистограммы

Равномерное преобразование гистограммы осуществляется по формуле

,

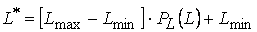(1)

где 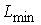, 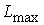- минимальное и максимальное значения элементов массива интенсивностей 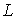исходного изображения;

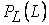- функция распределения вероятностей исходного изображения, которая аппроксимируется гистограммой распределения 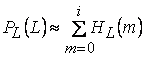. Другими словами, речь идет о кумулятивной гистограмме изображения.

В среде Matlab это можно реализовать следующим образом. Вычисляем кумулятивную гистограмму исходного изображения

CH=cumsum(H)./(N*M);

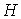- вектор значений гистограммы исходного изображения, а 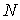, 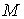- размеры данного изображения, которые определяются с помощью функции size

[N M]=size(L);

Далее, согласно формуле (1), определяем значения интенсивностей пикселей результирующего изображения.

L1(i,j)=CH(ceil(255*L(i,j)+eps));

figure, imshow(L1);

Значение eps используется вместе с функцией ceil для того, чтобы избежать присвоения индексам кумулятивной гистограммы 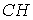нулевых значений. Результат применения метода равномерного преобразования гистограммы представлен на рис. 3.

Рис. 3. Исходное изображение, обработанное методом равномерного преобразования гистограммы.

Гистограмма, преобразованного согласно формуле (1) изображения, представлена на рис. 4. Она действительно занимает почти весь динамический диапазон и является равномерной.

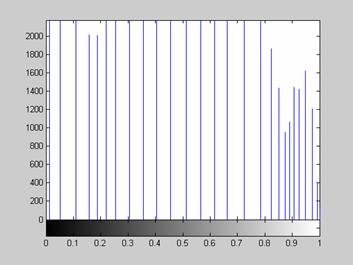
Рис. 4. Гистограмма изображения, представленного на рис. 3.

О равномерной передаче уровней интенсивностей элементов изображения свидетельствует также и его кумулятивная гистограмма (рис. 5).

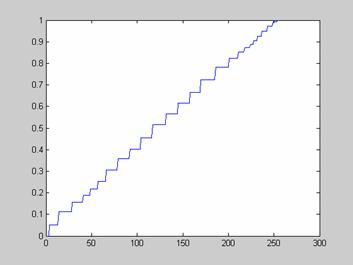
Рис.5. Кумулятивная гистограмма изображения, представленного на рис. 3.

Далее рассмотрим методы видоизменения гистограмм, которые аналогичны к рассмотренному подходу и будут отличаться только выражениями преобразования.