Законы алгебры логики. ❒Эксперимент 1: Коммутативные законы
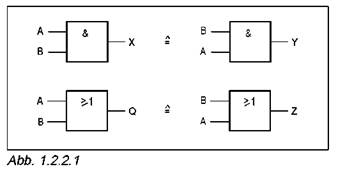 |
❒Эксперимент 1: Коммутативные законы
Проверьте справедливость коммутативных законов.
Ход работы:
· Заполните таблицу 1.2.2.1, внося выходные состояния логических схем, представленных на рисунке 1.2.2.1.
Запомни:
При подаче сигналов на входы элементов И и ИЛИ нет необходимости в соблюдении определенной очередности!
| И | ИЛИ | ||||
| A | B | X | Y | Q | Z |
| Таблица 1.2.2.1 Таблица истинности 2.1 Таблица истинности |
❒  Эксперимент 2: Ассоциативные законы
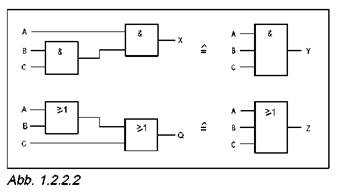
Эксперимент 2: Ассоциативные законы
Проверьте справедливость ассоциативных законов.
Ход работы:
· Заполните таблицу 1.2.2.2, внеся в нее выходные состояния логических схем, представленных на рисунке 1.2.2.2.
|
В схемах И и ИЛИ один логический элемент с большим количеством входов может быть собран из множества логических элементов с малым числом входов.
| И | ИЛИ | |||||
| A | B | C | X | Y | Q | Z |
Таблица 1.2.2.2 Таблица истинности
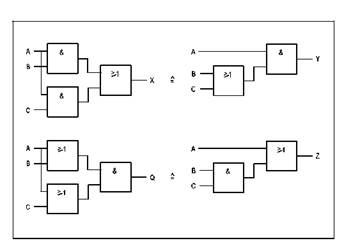 |
❒Эксперимент 3: Дистрибутивные законы
Проверьте справедливость дистрибутивных законов.
Ход работы:
· Заполните таблицу 1.2.2.3, в нее выходные состояния логических схем, представленных на рисунке 1.2.2.3.
Рисунок 1.2.2.3
Запомни:
Если соединенные по схеме ИЛИ или И термы И или ИЛИ содержат одинаковую переменную, то она может быть, аналогично общему множителю в математике, вынесена за скобки. Это позволяет экономить количество используемых логических элементов..
| A | B | C | X | Y | Q | Z |
| Таблица 1.2.2.3 Таблица истинности |
Примечания:
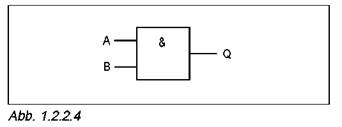 |
| ❒Эксперимент 4: Законы связи Проверьте справедливость закона связи на переменных величинах схемы на тождество в качестве дополнения или постоянной величины. |
Ход работы:
| Q как логическая величина | Q как переменная величина А или как постоянная величина | ||
| A | B | ||
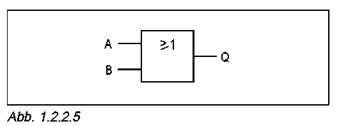
· Заполните таблицы 1.2.2.4 и 1.2.2.5, внося в нее выходные состояния логических схем, представленные на рисунках 1.2.2.4 и 1.2.2.5, сначала как логической величины, а потом как переменной А или постоянной величины.
Запомни:
Если схема И имеет больше входов, чем требуется, то неиспользуемые входы должны объединяться с используемыми входами или соединяться с уровнем, который соответствует значению 1.
|
Запомни:
В схеме ИЛИ лишние входы должны включаться с используемыми входами или соединяться с уровнем, который соответствует значению 0.
 |
| Q как логическая величина | Q как переменная величина А или как постоянная величина | ||
| A | B | ||
|
❒Эксперимент 5: Законы поглощения
Проверьте справедливость законов поглощения.
Ход работы:
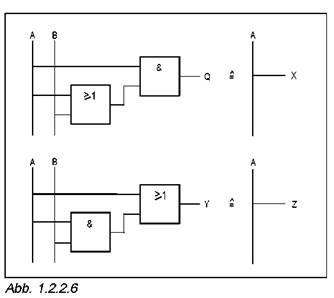
· Заполните таблицу 1.2.2.6, внося в нее выходные состояния логических схем, представленных на рисунке 1.2.2.6, сначала как логической величины, а потом как переменной величины.
Запомни:
Если термы ИЛИ или И соединены общей переменной по схеме И или ИЛИ, то на выходе имеет место значение общей переменной; благодаря этому возможно уменьшение аппаратных затрат.
|
| Логическая величина | Выход как переменная величина | |||||
| A | B | Q | X | Y | Z | |
| Таблица 1.2.2.6 Таблица истинности |
 |
❒ Эксперимент 6: Двойное отрицание
Проверьте справедливость закона двойного отрицания.
Ход работы:
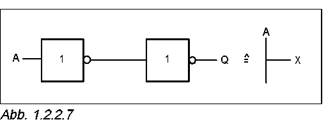
•Заполните таблицу 1.2.2.7, внося в нее выходные состояния логических схем, указанных на рисунке 1.2.2.6.
Запомни:
В цифровых микросхемах иногда требуется усилить сигнал или компенсировать время прохождения сигнала через определенные логические элементы. Для этого пригодны инверторы, поскольку после прохождения каждого второго инвертора сигнал вновь принимает свое исходное состояние.
| A | Q | X |
Таблица 1.2.2.7
❒Эксперимент 7: Законы Де Моргана
Проверьте справедливость законов Де Моргана.
Ход работы:
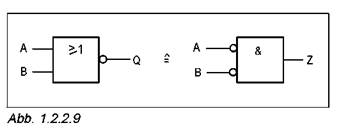
•Заполните таблицы 1.2.2.8 … 1.2.2.11, внося в нее выходные состояния логических схем, представленных на рисунках 1.2.2.8 … 1.2.2.11.
Запомни:
Законы Де Моргана позволяют реализовывать логические схемы только на основе элементов НЕ-И или НЕ-ИЛИ.
 |
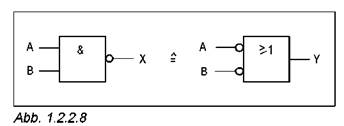 |
| A | B | X | Y |
| A | B | Q | Z |
Таблица 1.2.2.8
Таблица 1.2.2.9
 |
| A | B | R | S |
| A | B | M | N |
Таблица 1.2.2.10
Таблица 1.2.2.11
