Равноточные измерения

Приемы оценки случайных погрешностей прямых равноточных измерений стандартизованы и регламентируются ГОСТ 8.207—76. За результат измерения принимается оценка mх, вычисляемая по формуле (1.17). С увеличением n . 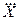Так как mx определяет среднее значение любой случайной величины, то при отсутствии систематических погрешностей mx=Q.Таким образом, mх, называемое средним арифметическим результатов наблюдений и обозначаемое чаще , является состоятельной, несмещенной и эффективной оценкой истинного значения измеряемой величины Q.

Случайная погрешность результата каждого наблюдения характеризуется, как уже указывалось, значением СКО σх. Поскольку при практических расчетах имеется возможность определять лишь значения

, (1.19)

называемые случайными отклонениями результатов отдельных наблюдений, то для расчета вместо (1.18) должна применяться следующая формула (ГОСТ 11.004—74):

. (1.20)

Аналогичным образом случайную погрешность результата измерения можно охарактеризовать значением СКО . Известно, что . Переходя к оценке и воспользовавшись формулой (1.20), находим:

(1.21)

Полученные точечные оценк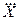и и хотя и позволяют оценить результат измерения и его случайную погрешность, но не содержат никаких сведений о вероятности данных оценок. Поэтому задача оценки случайных погрешностей не исчерпывается вычислением 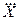и , и от точечных оценок мы должны перейти к так называемым интервальным оценкам, связанным с определением доверительных границ случайной погрешности результата измерения. Доверительные границы — это верхняя и нижняя границы интервала, внутри которого с заданной доверительной вероятностью Р находится погрешность результата измерения.

Если результаты наблюдений принадлежат распределениям (1.9) или (1.13), то для нахождения доверительных границ случайной погрешности результата измерения, обозначаемых 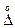, пользуются табличными значениями функций F(t) или F(t,n) соответственно. Так как распределение (1.13) более универсально, ГОСТ 8.207—76 рекомендует определять 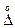с помощью коэффициента Стьюдента t. Количественная связь между 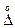и t записывается без учета знака в виде:

, (1.22)

При практических расчетах значение 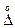следует определять для Р = 0,95. Если измерение нельзя повторить, ГОСТ 8.207—76 допускает принимать Р = 0,99. Поэтому в табл. 1.2 приведены значения t(n), заимствованные из таблицы F(t, n) для указанных значений Р.

Табл.1.2. Значение коэффициента t для распределения Стьюдента с (n-1) степенями свободы

n-1	P=0,95	P=0,99	n-1	P=0,95	P=0,99
	3,182	5,841		2,120	2,921
	2,776	4,604		2,101	2,878
	2,571	4,032		2,086	2,845
	2,447	3,707		2,074	2,819
	2,365	3,499		2,064	2,797
	2,306	3,355		2,056	2,779
	2,228	3,169		2,048	2,763
	2,179	3,055		2,043	2,750
	2,145	2,977	∞	1,960	2,576

Если сравнить значения t, рассчитанные для разных распределений (см. табл. 1.1), то оказывается, что при Р>0,85 значения t максимальны для нормального распределения. Поэтому при неизвестной функции распределения (или невозможности проверки принадлежности результатов наблюдений к нормальному распределению) рекомендуется считать нормальным, так как надежность оценки 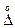повышается.

В заключение анализа приемов оценок случайных погрешностей прямых равноточных измерений рассмотрим так называемый критерий грубых погрешностей. Оказывается, что при n>30 и Р = 0,9973 из таблицы F(t) следует t = 3. Это значение t можно считать предельно возможным при определении 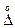по формуле (1.22), так как вероятность появления большего значения 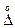равна всего лишь 0,0027. Поэтому в метрологической практике критерий «трех сигм» принят в качестве критерия грубых погрешностей (см. § 1.1.3). Если

, (1.23)

то такое наблюдение содержит грубую погрешность и должно быть исключено при обработке результатов наблюдений. При n<30 более достоверна оценка грубой погрешности, сделанная в соответствии с указаниями ГОСТ 11.002—72, регламентирующего правила оценки анормальности результатов наблюдений.