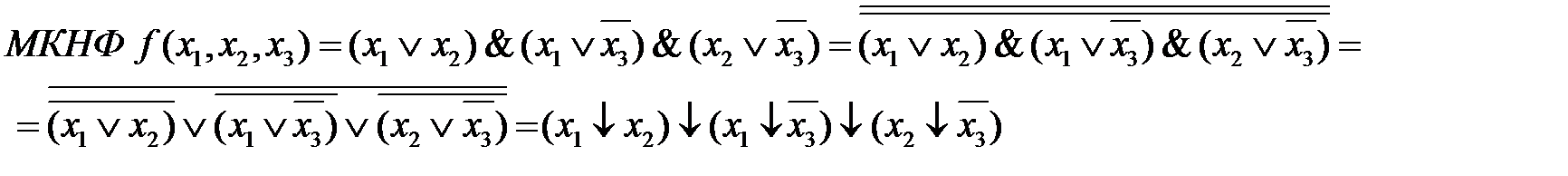Минимизация логических функций методом Квайна
Метод Квайна позволяет представлять функции с минимальным числом членов и минимальным числом символов в членах. Преобразование осуществляется в несколько этапов. Рассмотрим минимизацию логической функции, заданной таблицей 2.1.5.
Чтобы получить минимальную дизъюнктивную нормальную форму (МДНФ) необходимо:
1. Записать СДНФ функции, заданной таблицей
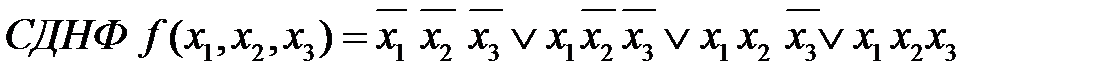
2. Выполнить операцию склеивания между членами, отличающимися в одном аргументе. Результатами склеивания будут одинаковые аргументы.
1-2 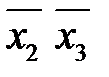
2-3 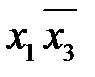
3-4 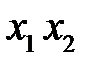
3. Результаты склеивания добавить в качестве дополнительных членов к исходной СДНФ и выполнить операцию поглощения. Результаты склеивания поглощают те члены, из которых они получились.

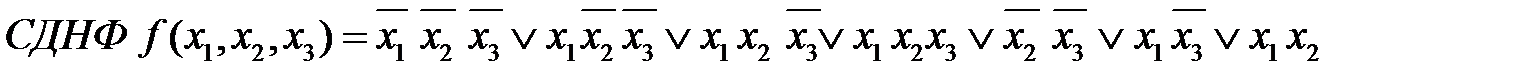
В результате получаем сокращенную ДНФ, члены которой называются простыми импликантами.
4. Построить импликантную матрицу, в столбцах которой записать члены исходной СДНФ, а в строках - простые импликанты. Звездочками отметить члены СДНФ, поглощаемые каждой простой импликантой.
| Простые импликанты | Члены СДНФ | |||
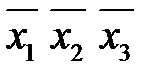 | 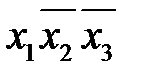 | 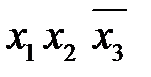 | 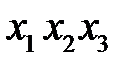 | |
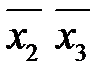 | * | * | ||
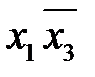 | * | * | ||
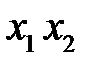 | * | * |
5. В МДНФ включить минимальное количество простых импликант (с минимальным количеством символов), обеспечивающих поглощение всех членов СДНФ.
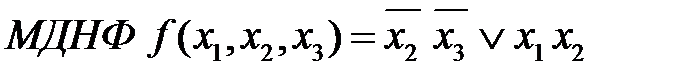
Чтобы получить МКНФ необходимо аналогичные преобразования выполнить над СКНФ.
Рассмотрим минимизацию логической функции, заданной таблицей 2.1.6.
Таблица 2.1.6. Таблица истинности функции.
| Х1 | ||||||||
| Х2 | ||||||||
| Х3 | ||||||||
| ƒ |
1. Записать СКНФ функции, заданной таблицей
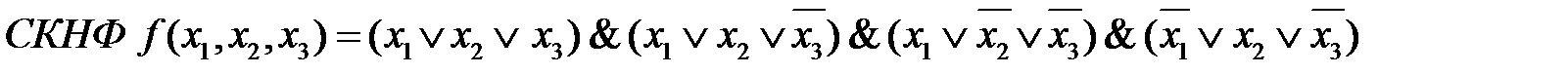 2. Выполнить операцию склеивания между членами, отличающимися в одном аргументе. Результатами склеивания будут одинаковые аргументы.
2. Выполнить операцию склеивания между членами, отличающимися в одном аргументе. Результатами склеивания будут одинаковые аргументы.
1-2 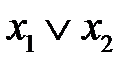
2-3 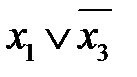
2-4 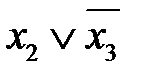
3. Результаты склеивания добавить в качестве дополнительных членов к исходной СДНФ и выполнить операцию поглощения. Результаты склеивания поглощают те члены, из которых они получились.

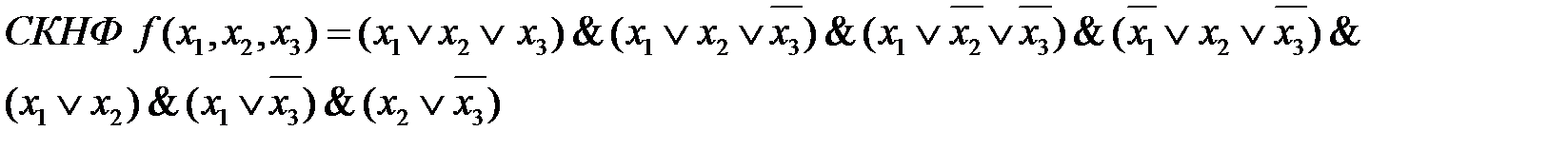
В результате получаем сокращенную КНФ, члены которой называются простыми импликантами.
4. Построить импликантную матрицу, в столбцах которой записать члены исходной СКНФ, а в строках- простые импликанты. Звездочками отметить члены СКНФ, поглощаемые каждой простой импликантой.
| Простые импликанты | Члены СКНФ | |||
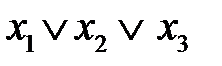 | 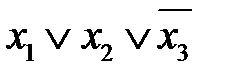 | 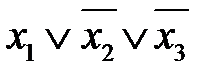 | 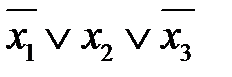 | |
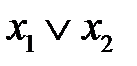 | * | * | ||
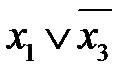 | * | * | ||
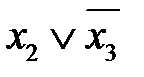 | * | * |
5. В МКНФ включить минимальное количество простых импликант (с минимальным количеством символов), обеспечивающих поглощение всех членов СКНФ.
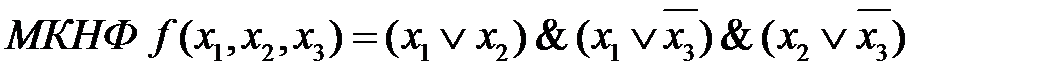
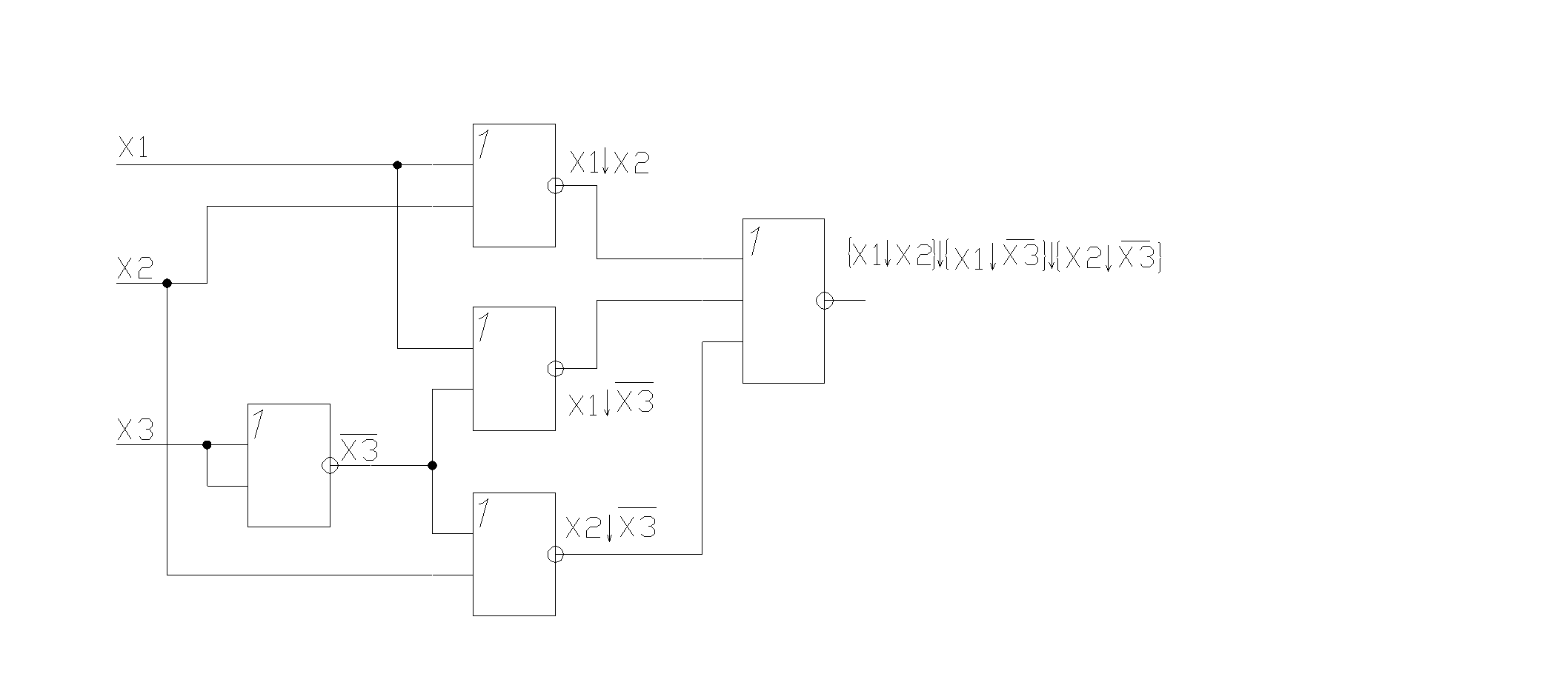
Синтез логических устройств в базисах «ИЛИ-НЕ», «И-НЕ»
Рассмотрим последовательность синтеза логического устройства на примере функций, полученных в разделе 2.1.2.
Чтобы построить схему в базисе «И-НЕ» необходимо получить МДНФ, дважды ее проинвертировать, одну инверсию раскрыть по правилу Моргана, записывая логическое выражение через операцию”И НЕ“.
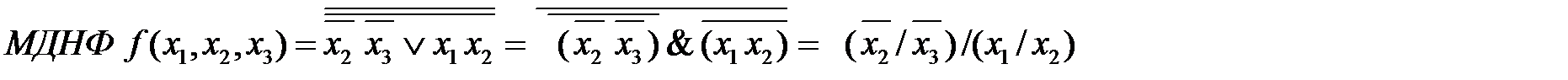
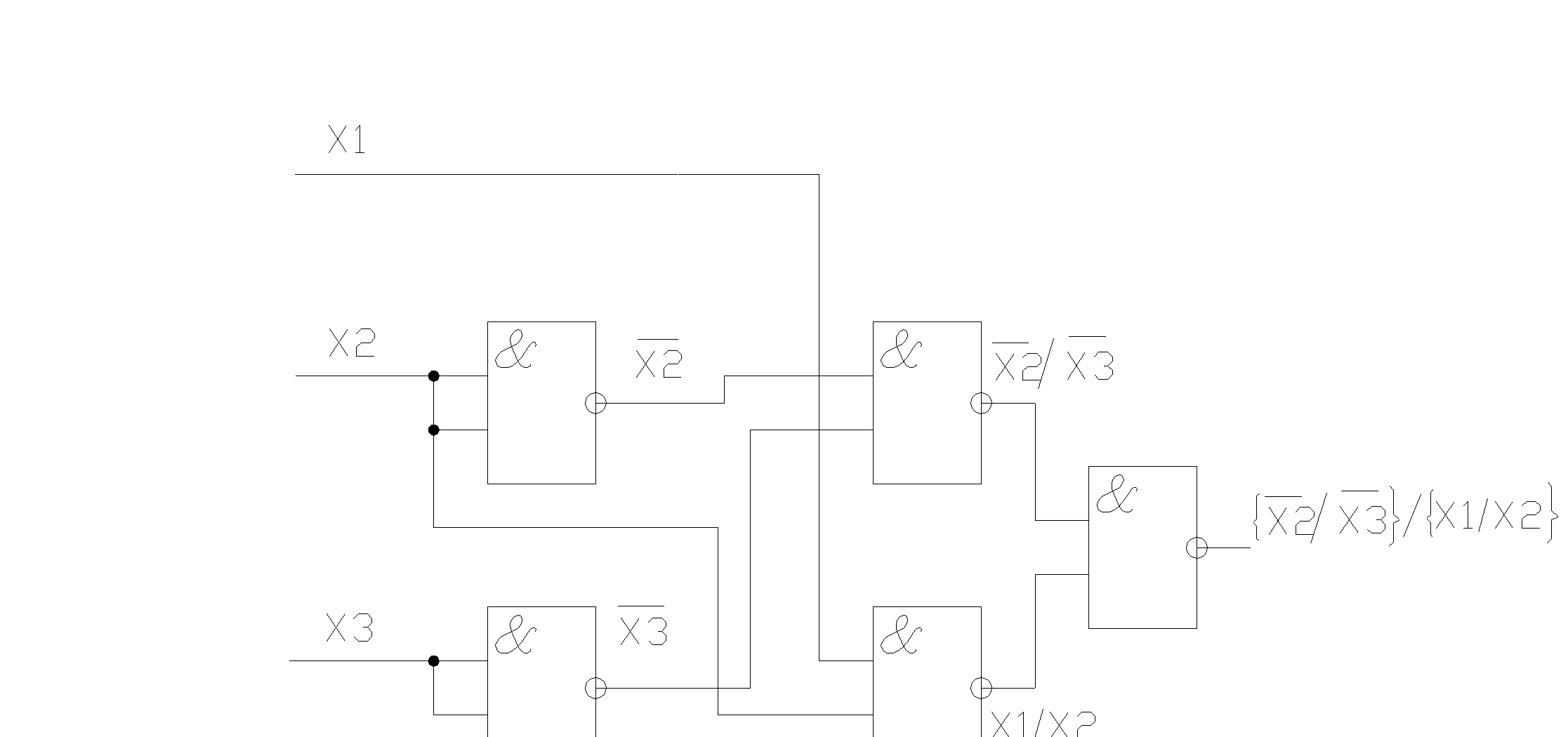
Чтобы построить схему в базисе «ИЛИ-НЕ», необходимо получить МКНФ, дважды ее проинвертировать и одну инверсию раскрыть по правилу Моргана, записывая логическое выражение через операцию «ИЛИ-НЕ».