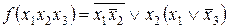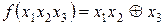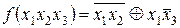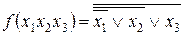Стандартные формы функций алгебры логики

К стандартным формам функций алгебры логики относятся:

- дизъюнктивная нормальная форма (ДНФ),

- совершенная дизъюнктивная нормальная форма (СДНФ),

- конъюнктивная нормальная форма (КНФ),

- совершенная конъюнктивная нормальная форма (СКНФ).

Наибольшее применение при синтезе и анализе дискретных устройств находят стандартные формы ДНФ и СДНФ. К этим формам предъявляются следующие требования:

1. Формы должны быть такими, чтобы ими можно было представить любую ФАЛ.

2. Алгоритм представления ФАЛ в этих формах не должен быть сложным.

3. Представленная в любой из указанных форм ФАЛ при необходимости должна легко поддаваться преобразованиям с целью упрощения (сокращению числа аргументов).

Дизъюнктивная нормальная форма представляет собой дизъюнкцию элементарных конъюнкций аргументов, например

.

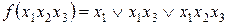Элементарной конъюнкцией называется логическое произведение любого конечного числа различимых между собой аргументов с отрицаниями или без них. Элементарная конъюнкция может состоять из одного аргумента, двух и более в зависимости от числа аргументов от которых зависит функция.

Любая функция алгебры логики может быть представлена в виде ДНФ согласно следующего алгоритма:

1. Путем преобразований (используя таблицу 1.6.) в заданном логическом выражении оставить только операции «И», «ИЛИ», «НЕ».

2. Опустить знаки отрицания непосредственно на аргументы.

3. Раскрыть скобки, если они имеют место.

4. Отбросить лишние аргументы в конъюнкциях согласно закону повторения.

5. Если имеют место одинаковые элементарные конъюнкции, то лишние отбросить.

~

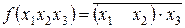Пример 2.6. . Представить заданное логическое выражение в ДНФ.

Решается согласно алгоритма

1. Необходимо избавиться от операции равнозначности, используя таблицу 1.6.

.

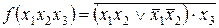2. Опускаются знаки отрицания непосредственно на аргументы

.

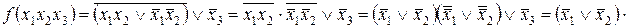
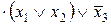3. Раскрываются скобки

.

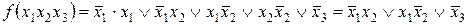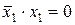
Лишних аргументов в конъюнкциях и повторяющихся конъюнкций нет.

Совершенной дизъюнкцией нормальной формой функций алгебры логики называется дизъюнкция конституент единицы.

Конституентой единицы называется элементарная конъюнкция, содержащая все аргументы данной функции, причем сама функция на данном наборе аргументов принимает значение 1. Например

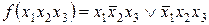
в данном случае функция зависит от трех аргументов х₁х₂х₃.

Все слагаемые содержат по три аргумента с отрицаниями или без них. Функцию алгебры логики заданную в виде ДНФ можно представить в СДНФ (кроме теоремы разложения) двумя способами аналитическим или табличным.

Аналитический способ представления ДНФ в СДНФ заключается в использовании двух тождеств 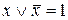и 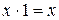, т.е. сумма аргумента с его отрицанием всегда равна единице, а умножение любой функции алгебры логики на единицу не меняет ее значения. В элементарных конъюнкциях ДНФ отсутствуют некоторые аргументы от которых зависит функция, например

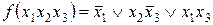
Для преобразования данной ДНФ в СДНФ необходимо во все элементарные конъюнкции ввести недостающие аргументы путем умножения их на тождества 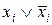, где i – недостающий аргумент.

Пример 2.7. Преобразовать ДНФ 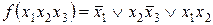в СДНФ.

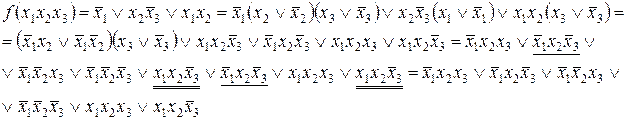
Отсюда следует, что для преобразования ДНФ в СДНФ необходимо:

1. Все элементарные конъюнкции ДНФ умножить на тождества 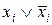с недостающими аргументами.

2. Раскрыть скобки.

3. Отбросить лишние слагаемые (конституэнты единицы).

Табличный способ представления ДНФ в СДНФ предусматривает использование таблицы истинности заданной функции, в которую добавляется столбец с констуентами единицы.

Пример 2.8. Представить функцию алгебры логики в СДНФ табличным способом 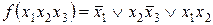(функция та же, что и в примере 2.7).

Таблица 2.4.

Таблица истинности заданной функции

Наборы аргументов		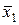		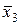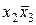х1х2		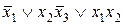Конституэнты единицы
х1х2х3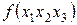
0 0 0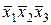
0 0 1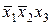
0 1 0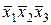
0 1 1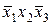
1 0 0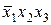
1 0 1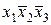
1 1 0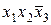
1 1 1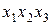

Из таблицы 2.4. следует, что каждая конституента равна единице только на своем наборе. Для получения СДНФ заданной функции необходимо из таблицы 2.4. в качестве слагаемых СДНФ записать все конституенты единицы на которых функция равна единице. В результате получим следующую СДНФ заданной функции

.

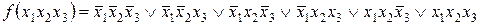Полученная СДНФ совпадает с СДНФ примера 5.2.

Контрольные вопросы

1. Представить и пояснить тождества алгебры логики.

2. Представить и пояснить законы алгебры логики.

3. Доказать закон склеивания.

4. Доказать соотношения, вытекающие из теоремы разложения.

5. Что представляет собой функционально-полный набор функций алгебры логики?

6. Назвать возможные функционально-полные наборы (базисы) ФАЛ.

7. Дать определение ДНФ.

8. Что представляет собой элементарная конъюнкция?

9. Дать определение СДНФ.

10. Что представляет собой конституента единицы?

11. Какие существуют способы представления ДНФ в СДНФ?

12. Решить примеры упрощения логических выражений используя законы и тождества ФАЛ, а также соотношения, вытекающие из теоремы разложения

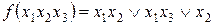
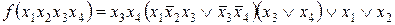
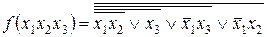
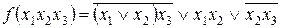
13. Решить пример представления заданных ФАЛ функционильно-полными наборами «И», «ИЛИ», «НЕ»; «И-НЕ»; «ИЛИ-НЕ»

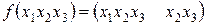
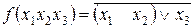
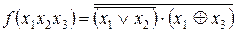
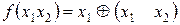
14. Решить примеры представления заданных функций сначала в виде ДНФ, а затем в виде СДНФ