Виды распределения результатов наблюдения и случайных погрешностей

Случайная погрешность измерения образуется под влиянием большого числа факторов, сопутствующих процессу измерения. В каждой конкретной ситуации работает свой механизм образования погрешности. Поэтому естественно предположить, что каждой ситуации должен соответствовать свой тип распределения погрешности. Однако во многих случаях имеются возможности еще до проведения измерений сделать некоторые предположения о форме функции распределения, так что после проведения измерений остается только определить значения некоторых параметров, входящих в выражение для предполагаемой функции распределения.

Случайная погрешность характеризует неопределенность наших знаний об истинном значении измеряемой величины, полученных в результате проведенных наблюдений. Согласно К. Шеннону мерой неопределенности ситуации, описываемой случайной величиной X, является энтропия [4]

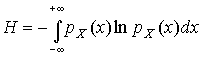
являющаяся функционалом дифференциальной функции распределения 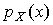. Можно предположить, что любой процесс измерения формируется таким образом, что неопределенность результата наблюдений оказывается наибольшей в некоторых пределах, определяемых допускаемыми значениями погрешности. Поэтому наиболее вероятными должны быть такие распределения 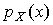, при которых энтропия обращается в максимум.

Для выявления вида наиболее вероятных распределений рассмотрим несколько наиболее типичных случаев [3].

1. В классе распределений результатов наблюдений 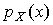, обладающих определенной зоной рассеивания между значениями х = b и х = а шириной b-а=2а, найдем такое, которое обращает в максимум энтропию 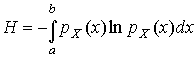при наличии ограничивающих условий:
, , ,
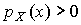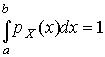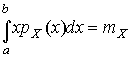где 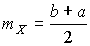- математическое ожидание результатов наблюдений. Решение поставленной задачи находится методом множителей Лагранжа.

Искомая плотность распределения результатов наблюдений описывается выражением

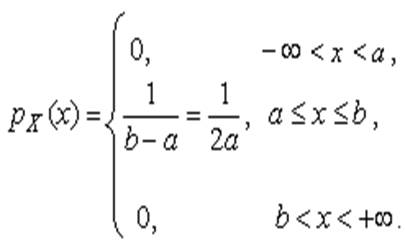(23)

Такое распределение результатов наблюдений называется равномерным.

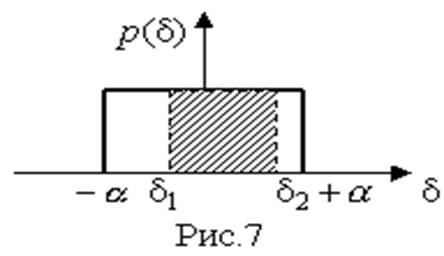
Значения дифференциальной функции распределения равномерной распределенной случайной погрешности постоянны в интервале [- а; + а], а вне этого интервала равны нулю (рис.6).

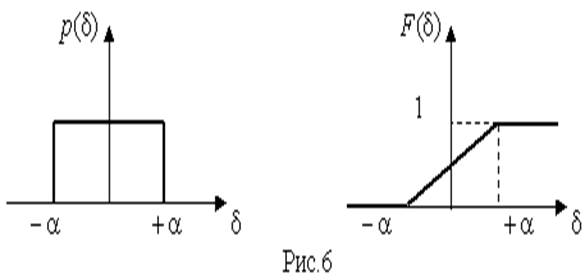
Поэтому выражение для дифференциальной функции распределения случайной погрешности можно записать в виде

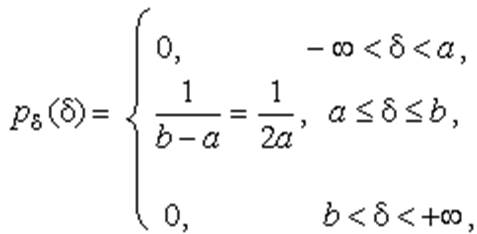(24)

Определим числовые характеристики равномерного распределения. Математическое ожидание случайной погрешности находим по формуле (10):

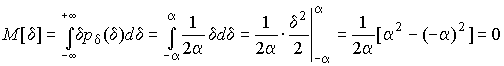
Дисперсию случайной равномерно распределенной погрешности можно найти по формуле (18):

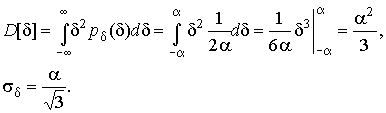
В силу симметрии распределения относительно математического ожидания коэффициент асимметрии должен равняться нулю:

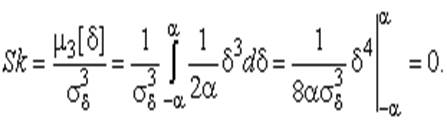
Для определения эксцесса найдем вначале четвертый момент случайной погрешности:

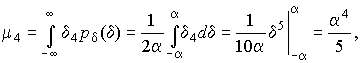
поэтому

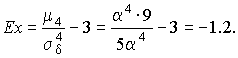
В заключение найдем веро-ятность попадания случайной погрешности в заданный интервал [ 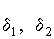], равный заштрихованной площади на рис.7.

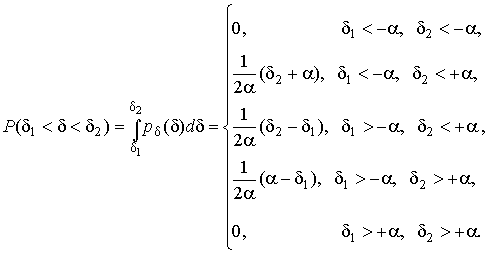
2. В классе распределений результатов наблюдений 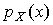, обладающих определенной дисперсией 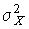, найдем такое, которое обращает в максимум энтропию 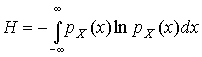при наличии ограничений:

, , , .

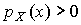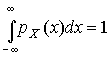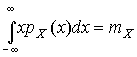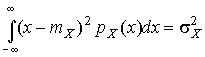Решение этой задачи также находится методом множителей Лагранжа. Искомая плотность распределения результатов наблюдений описывается выражением

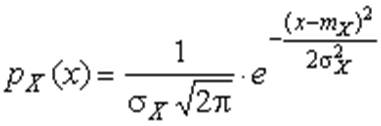(25)

где 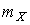- математическое ожидание и 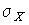- среднеквадратическое отклонение результатов наблюдений.

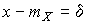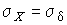Учитывая, что при полном исключении систематических погрешностей и , для дифференциальной функции распределения случайной погрешности можно записать уравнение

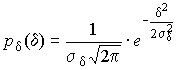(25)

Распределение, описываемое уравнениями (25) и (26), называется нормальным или распределением Гаусса.

На рис.8 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения .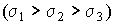

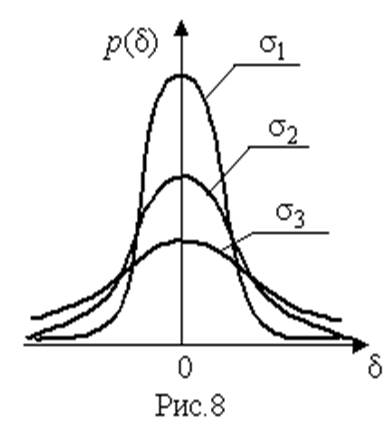
Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений.

Вычислим вероятность попадания результата наблюдения в некоторый заданный интервал :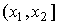

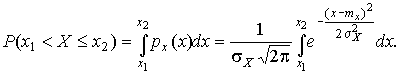
Заменим переменные:

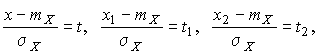
после чего получим следующее выражение для искомой вероятности:

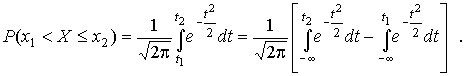
Интегралы, стоящие в квадратных скобках, не выражаются в элементарных функциях, поэтому их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией

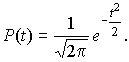(27)

В приложении (табл.П.5 и П.6) приведены значения дифференциальной функции нормированного нормального распределения, а также интегральной функции этого распределения, определяемой как

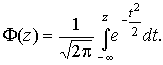(28)

С помощью функции Ф(z) вероятность 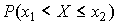находят как

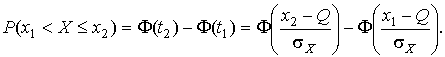(29)

При использовании данной формулы следует иметь в виду тождество

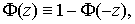
вытекающее непосредственно из определения функции Ф(z).

Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики - Муавр, Лаплас, Гаусс, Чебышев и Ляпунов. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

3. Предположим, что результаты наблюдений распределены нормально, но их среднеквадратическое отклонение является величиной случайной, изменяющейся от опыта к опыту. Такое предположение более осторожное, чем предположение о неизменности 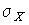в течение всего времени измерений. В этом случае, рассуждая таким же образом, как и прежде, легко найти, что энтропия обращается в максимум, если результаты наблюдений имеют распределение Лапласа с плотностью

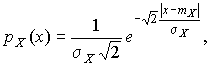(30)

где 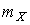- математическое ожидание, 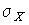- среднеквадратическое отклонение результатов наблюдения. Распределением Лапласа следует пользоваться в тех случаях, когда точностные характеристики заранее неизвестны или нестабильны во времени.

Дифференциальная функция распределения случайных погрешностей получается подстановко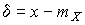й и 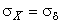в выражение (30):

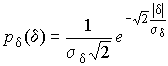
Асимметрия распределения равна нулю, поскольку распределение симметрично относительно нуля, а эксцесс в соответствии с формулой (22) составляет

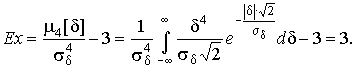
Таким образом, по сравнению с нормальным распределением (Ех = 0) равномерное распределение является более плосковершинным (Ех = -1.2), а распределение Лапласа - более островершинным (Ех = 3).