Упражнение 2 (устно)

Еще один пример. На экзамен приготовлено 30 билетов. Чему равно количество событий, которые могут произойти при вытягивании билета? (30)

- Равновероятны эти события или нет? (Равновероятны.)

- Чему равна неопределенность знаний студента перед тем как он вытянет билет? (30)

- Во сколько раз уменьшится неопределенность знания после того как студент билет вытянул? (В 30раз.)

- Зависит ли этот показатель от номера вытянутого билета? (Нет, т.к. события равновероятны.)

Из всех рассмотренных примеров можно сделать следующий вывод:

Чем больше начальное число возможных равновероятных событий, тем в большее количество раз уменьшается неопределенность наших знаний, и тем большее количество информации будет содержать сообщение о результатах опыта.

А каким может быть самое маленькое количество информации? Вернем­ся к примеру с монетой. Предположим, что у монеты обе стороны «орел».

- Существует ли неопределенность знаний пред броском в этом случае? Почему? (Нет, так как мы заранее знаем, что выпадет в любом случае «орел».)

- Получите вы новую информацию после броска? (Нет, так как ответ мы уже знали заранее.)

- Будет ли информативным сообщение о результате броска? (Нет, так оно не принесло новых и полезных знаний.)

- Чему равно количество информации в этом случае? (Нулю, т.к. оно неинформативно.)

Вывод: мы не получаем информации в ситуации, когда происходит одно событие из одного возможного. Количество информации в этом случае равно нулю.

Для того чтобы количество информации имело положительное значение, необходимо получить сообщение о том, что произошло событие как минимум из двух равновероятных. Такое количество информации, которое находится в сообщении о том, что произошло одно событие из двух равновероятных, принято за единицу измерения информации и равно 1 биту.

Огромное количество способов кодирования информации неизбежно привело пытливый ум человека к попыткам создать универсальный язык или азбуку для кодирования. Эта проблема была достаточно успешно реализована лишь в отдельных областях техники, науки и культуры. Своя система кодирования информации существует и в вычислительной технике. Она называется двоичным кодированием. Всю информацию, с которой работает вычислительная техника, можно представить в виде последовательности всего двух знаков – 1 и 0. Эти два символа называются двоичными цифрами, по-английски – binary digit или сокращенно bit – бит.

1 бит кодирует 2 понятия или сообщения (0 или 1)

2 бита – 4 разных сообщения (00 или 01 или 10 или 11)

3 бита – 8 разных сообщений

4 бита – 16 разных сообщений и т.д.

Общая формула

,

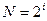где N – количество значений информации, i – количество бит.

Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 – есть сигнал, 0 – нет сигнала. Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.

Итак, с помощью битов информация кодируется. С точки зрения коди­рования с помощью 1 бита можно закодировать два сообщения, события или два варианта некоторой информации. С точки зрения вероятности 1 бит — это такое количество информации, которое позволяет выбрать одно событие из двух равновероятных. Согласитесь, что эти два определения не противоречат друг другу, а совершенно одинаковы, но просто рассмотрены с разных точек зрения.

Еще одно определение 1 бита:

1 бит - это количество информации, уменьшающее неопределенность знаний в два раза.

Игра «Угадай число»

Загадайте число из предложенного интервала.

Стратегия поиска:

Необходимо на каждом шаге в два раза уменьшать неопределенность знания, т.е. задавать вопросы, делящие числовой интервал на два. Тогда ответ «Да» или «Нет» будет содержать 1 бит информации. Подсчитав общее ко­личество битов (ответов на вопросы), найдем полное количество информации, необходимое для отгадывания числа.

Например, загадано число 5 из интервала от 1 до 16 (неопределенность знаний перед угадыванием равна 16).

Вопрос	Ответ	Неопределенность знаний	Полученное количест­во информации
Число больше 8?	Нет		1 бит
Число больше 4?	Да		1бит
Число больше 6?	Нет		1бит
Число 5?	Да		1 бит
Итого:			4 бита

Вывод: количество информации, необходимое для определения одного из 16 чисел, равно 4 бита.

Существует формула, которая связывает между собой количество возможных событий и количество информации:

,

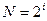где N — количество возможных вариантов, i - количество информации.

Пояснение: формулы одинаковые, только применяются с разных точек зрения - кодирования и вероятности.

Если из этой формулы выразить количество информации, то получится

.

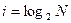Как пользоваться этими формулами для вычислений:

- если количество возможных вариантов N является целой степенью числа 2, то производить вычисления по формуле 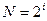достаточно легко. Вернемся к примеру: N = 32, i = 5, т.к. ;

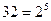- если же количество возможных вариантов информации не является целой степенью числа 2, т.е. если количество информации число ве­щественное, то необходимо воспользоваться калькулятором или сле­дующей таблицей.

Количество информации в сообщении об одном из N равновероятных событий: .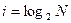

N	i	N	i	N	i	N	i
	0,00000		4,08746		5,04439		5,61471
	1,00000		4,16993		5,08746		5,64386
	1,58496		4,24793		5,12928		5,67243
	2,00000		4,32193		5,16993		5,70044
	2,32193		4,39232		5,20945		5,72792
	2,58496		4,45943		5,24793		5,75489
	2,80735		4,52356		5,28540		5,78136
	3,00000		4,58496		5,32193		5,80735
	3,16993		4,64386		5,35755		5,83289
	3,32193		4,70044		5,39232		5,85798
	3,45943		4,75489		5,42626		5,88264
	3,58496		4,80735		5,45943		5,90689
	3,70044		4,85798		5,49185		5,93074
	3,80735		4,90689		5,52356		5,95420
	3,90689		4,95420		5,55459		5,97728
	4,00000		5,00000		5,58496		6,00000

Например: Какое количество информации можно получить при угадыва­нии числа из интервала от 1 до 11? В этом примере N=11. Чтобы найти i (количество информации), необходимо воспользоваться таблицей. По таблице i = 3,45943 бит.