Шаг 6: Гиперболическое преобразование гистограммы

Гиперболическое преобразование гистограммы реализуется согласно формуле

,

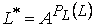(5)

где 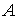- некоторая константа, относительно которой осуществляется гиперболическое преобразование гистограммы. Фактические параметр 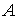равен минимальному значению интенсивности элементов изображения.

В среде Matlab этот метод может быть реализован следующим образом

L5(i,j)=.01^(CH(ceil(255*L(i,j)+eps))); % в данном случае А=0,01

figure, imshow(L5);

Рис. 15. Исходное изображение, обработанное методом гиперболического преобразования.

Гистограмма распределения интенсивностей элементов обработанного таким образом изображения представлена на рис. 16.

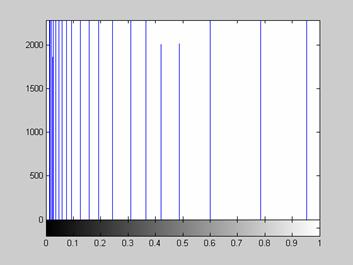
Рис. 16. Гистограмма изображения, обработанного методом гиперболического преобразования.

Кумулятивная гистограмма, форма которой соответствует характеру проводимых преобразований, представлена на рис. 17.

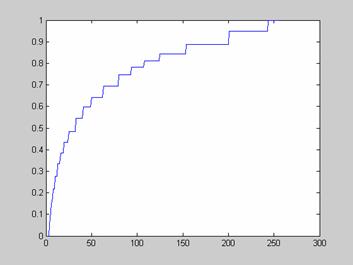
Рис. 17. Кумулятивная гистограмма изображения, обработанного методом гиперболического преобразования.

В данной работе были рассмотрены некоторые методы видоизменения гистограмм. Результатом применения каждого метода является то, что гистограмма распределения яркостей элементов обработанного изображения принимает определенную форму. Такого рода преобразования могут применяться для устранения искажений при передаче уровней квантирования, которым были подвергнуты изображения на этапе формирования, передачи или обработки данных.

Отметим также, что рассмотренные методы могут быть реализованы не только глобально, но и в скользящем режиме. Это приведет к усложнению вычислений, поскольку нужно будет анализировать гистограмму на каждом локальном участке. Однако, с другой стороны, такие преобразования, в отличие от глобальной реализации, позволяют увеличивать детальность локальных участков.

Подавление шумов на изображениях

Довольно часто при формировании визуальных данных результирующие изображения получаются зашумленными. Это объясняется несовершенством аппаратуры, влиянием внешних факторов и т.п. В конечном результате это приводит к ухудшению качества визуального восприятия и снижению достоверности решений, которые будут приниматься на основе анализа таких изображений. Поэтому актуальной является задача устранения или снижения уровня шумов на изображениях. Решению задачи фильтрации шумов посвящено очень много работ, существуют различные методы и алгоритмы. В этой работе рассмотрим только некоторые подходы и возможности их реализации в системе Matlab.

Содержание:

Шаг 1: Считывание исходного изображения.

Шаг 2: Формирование зашумленных изображений.

Шаг 3: Использование медианного фильтра для устранения импульсного шума.

Шаг 4: Подавление шумовой составляющей с использованием операции сглаживания.

Шаг 5: Пороговый метод подавления шумов.

Шаг 6: Низкочастотная фильтрация с использованием шумоподавляющих масок.