КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Результат измерения какой-либо величины зависит от многих факторов, влияние которых заранее учесть невозможно

Результат измерения какой-либо величины зависит от многих факторов, влияние которых заранее учесть невозможно. Значения, полученные в результате прямых измерений какого-либо параметра, являются случайными. Если число измерений одного и того же параметра велико, то в распределении его значений обнаруживаются некоторые закономерности. Использование методов математической статистики для обработки результатов измерений позволяет установить эти закономерности.

Статистической совокупностьюназывается совокупность объектов, характеризующаяся наличием некоторого общего признака. Наиболее полная совокупность, которая включает в себя все объекты, обладающие данным признаком, является генеральной совокупностью.

Провести изучение (измерение) всей генеральной совокупности, как правило, не представляется возможным, поэтому для исследования берут часть ее объектов, которые образуют выборочную совокупность, или выборку. В зависимости от числа объектов (объема выборки) п различают большую (п ≥ 30) и малую (п ≤ 30) выборки.

Наблюдаемые значения членов выборки называются вариантами. При проведении большого числа измерений значения измеряемой величины повторяются, поэтому число вариант к ≤ п. Число m_i наблюдений варианты х_i, называется частотой данной варианты.

Относительной частотой P_i* называется величина, равная отношению частоты m_i данной варианты к общему числу п значений измеряемой величины:

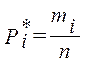(2.1)

Данные, получаемые при проведении экспериментов, представляют в виде статистических рядов. Значения величины X в выборке, записанные в последовательности измерений, составляют простой статистический ряд. Располагая полученные значения в последовательности их возрастания (или убывания), получают ранжированный ряд:

х₁≤ х₂≤…≤ х _n

Точечное (дискретное) статистическое распределение (вариационный ряд) — это статистическое распределение, состоящее из вариант и соответствующих им частот и относительных частот (табл.1).

Таблица 1

X	х1	х2	…	х i	…	х k
M	m1	m2	…	mi	…	mk
P*	P1*	P2*	…	Pi*	…	Pk*

Для составления интервального (непрерывного) статистического распределения весь диапазон значений величины Х делят на равные по величине интервалы x_i-1…x_i и указывают m_i —сумму частот вариант, попавших в каждый интервал, и Р* — сумму относительных частот (табл.2).

Таблица 2

xi-1-xi	1			…	n
mi
Pi*

Ширина интервала ,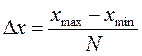

гдеx_max и х_min — наибольшее и наименьшее значения измеряемой величины соответственно; N — число интервалов, определяемое по формуле

N=3,3lgn+1 (2.2)

Графически статистическое распределение изображают в виде полигона частот и гистограммы. Для построения полигона частот (графика вариационного ряда) по оси абсцисс откладывают варианты х, а по оси ординат — значения частот т или относительных частот Р*, полученные точки соединяют ломаной линией (рис.2.1).

Гистограммустроят по данным интервального статистического распределения. Она представляет собой совокупность смежных прямоугольников, основанием которых является отрезок оси абсцисс, равный ширине интервала ∆х, а высота равна отношению Р* длякаждого интервала к ∆х (рис. 2.2).

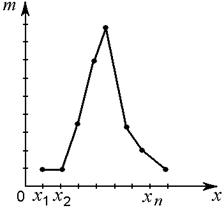
Рис. 2.1 Полигон частот величины х

Числовыми характеристиками распределения для выборки являются выборочная средняя, медиана, мода, выборочная дисперсия, выборочное среднее квадратическое отклонение.

Выборочная средняя 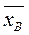— это величина, равная среднему ариф­метическому значению вариант статистического ряда: 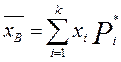или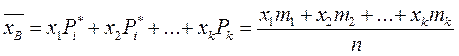

Медиана Me— это такое значение случайной величины, которое делит ранжированный статистический ряд пополам (по числу членов). Таким образом, вероятность Р того, что значение случайной величины меньше медианы, равна вероятности того, что значение случайной величины больше медианы: P(x<Me)= P(x>Me)=0,5.

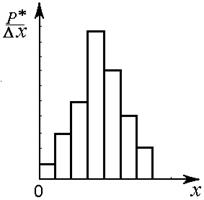
Рис. 2.2 Гистограмма величины х

Мода Mo равна варианте, которой соответствует наибольшая частота.

Выборочная дисперсия характеризует рассеяние вариант вокруг выборочной средней:

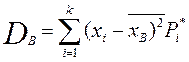
Выборочное среднее – квадратическое отклонение δ_B равно корню квадратному из выборочной дисперсии:

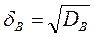
В теории вероятностей изучают случайные события и величины. Случайной величинойназывается такая величина, значения которой зависят от стечения случайных обстоятельств, в частности результат измерений какого-либо параметра. Степень возможности получения значения случайной величины характеризуется вероятностью данного значения.

Пусть в п опытах измеряемая величина т раз приняла некоторое значение х, тогда отношение т к п называется относительной частотой*этого значения: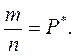

При небольшом числе опытов относительная частота значений в значительной мере имеет случайный характер и может заметно изменяться от одной группы опытов к другой. Однако при увеличении числа опытов она все более теряет свой случайный характер и приближается к некоторой постоянной величине — стати­стической вероятности события.

Статистической вероятностью Р событияназывают предел, к которому стремится его относительная частота при неограниченном увеличении числа измерений:

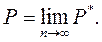
Практически за вероятность принимают относительную частоту значения при большом числе испытаний. Различают дискретные и непрерывные случайные величины.

Дискретнаявеличина принимает счетное множество значений, а непрерывная— любые значения внутри некоторого интервала.

Случайная величина считается заданной, если указано ее распределение. Для дискретной величины распределение— это совокупность значений деланной величины и соответствующих им вероятностей Р.

При задании закона распределения непрерывной величины используют две функции: плотность вероятности и функцию распределения случайной величины.

Плотность вероятности f(x) равна отношению dР — вероятности того, что значение случайной величины находится в интервале от х до х + dx, к величине dx этого интервала:

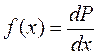(2.1)

Для определения вероятности попадания значения случайной величины в некоторый интервал (ab) необходимо проинтегрировать выражение (2.1) в соответствующих пределах:

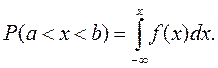Функция распределения F(x)случайной величины равна вероятности того, что случайная величина X принимает значения, меньшие х:

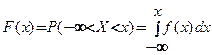
Существует множество законов распределения случайных величин. Одним из наиболее распространенных и общих является нормальный закон распределения, характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным (рис.2.3). Плотность вероятности для нормального закона распределения определяется по следующей формуле:

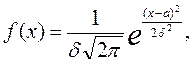где δ — среднее квадратическое отклонение;

а — математическое ожидание случайной величины.

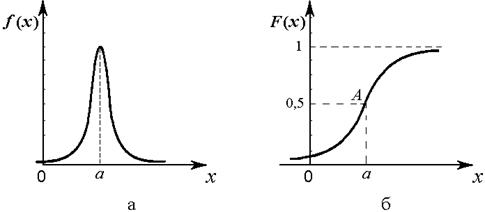
Рис. 2.3 Нормальный закон распределения: а – график плотности вероятности f(х); б – график функции распределения F(x)

График плотности вероятности f(х) (рис. 2.1, a) симметричен относительно прямой х = а, так как отклонения случайной величины вправо и влево от а равновероятны. При х →±∞ кривая асимптотически приближается к оси абсцисс. Максимальное значение плотность вероятности принимает при х = а.

График функции распределения F(x) (рис. 2.1, б) симметричен относительно точки А (а; 0,5). При х→-∞ функция F(x) →0; при х→+∞ функция F(x)→1.

Задание.

Получить у преподавателя указания и перечень объектов измерения.

3.1. Собрать 100 результатов измерений для статистического ряда.

3.2. Провести статистическую обработку опытных данных..