Оценка точности результатов измерений с использованием вероятностных функций

Результаты измерений и их погрешности являются случайными величинами. Для оценки случайных величин используют вероятностно- статистические методы, причем, решается задача об оценке вероятности появления погрешностей, не превышающих предельно допустимую величину.

Статистическими параметрами, используемыми при анализе результатов,являются:

- определяют центр группирования результатов

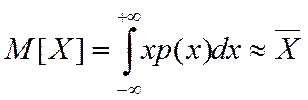
Мода, модальное значение

Медиана меd=

- определяющие поле рассеяния: среднеквадратическое отклонение (стандартное отклонение), дисперсия

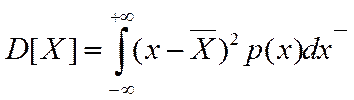
Вероятности появления случайных событий определяются:

1. интегральными функциями распределения вероятностей ;-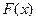

2. На практике чаще пользуются производной от интегральной функции распределения, эту производную называют дифференциальной функцией распределения или плотностью распределения вероятности :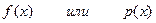

вероятность 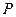того, что случайная величина 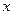принимает значения в некотором интервале 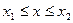записывается в виде

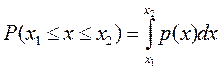
где 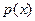называется плотностью распределения вероятности случайной величины .

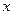Поскольку 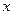находится в интервале 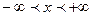с вероятностью равной единице

.

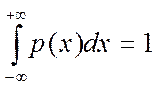Для оценки точности необходимо знать закон распределения случайной величины (в данном случае – параметра или его погрешности), т.е. взаимосвязь между возможными значениями погрешностей и соответствующими им вероятностями.

Обе вероятностные функции являются математическими моделями эмпирических законов распределения, получаемых из экспериментальных данных методами математической статистики, они дают исчерпывающее описание результата измерения.

Пример.

Экспериментальное построение вероятностных функций

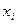, лк	Частота	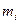Вероятность появления результата, 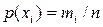, дифференц. функция распред. .вероятности	Вероятность того, что предыдущий результат будет меньше последующего или равен ему 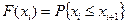, интегральная функция распред.вероятности
90,10		0,01	0,01
90,11		0,02	0,03
90,12		0,05	0,08
90,13		0,10	0,18
90,14		0,20	0,38
90,15		0,24	0,62
90,16		0,19	0,81
90,17		0,11	0,92
90,18		0,05	0,97
90,19		0,02	0,99
90,20		0,01	1,00

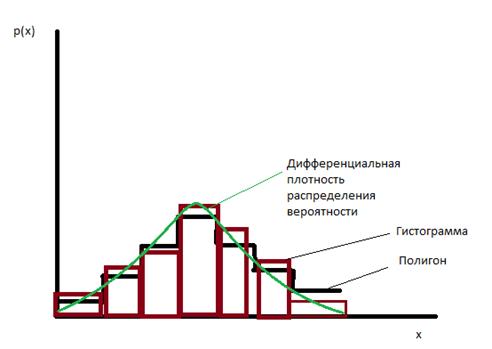
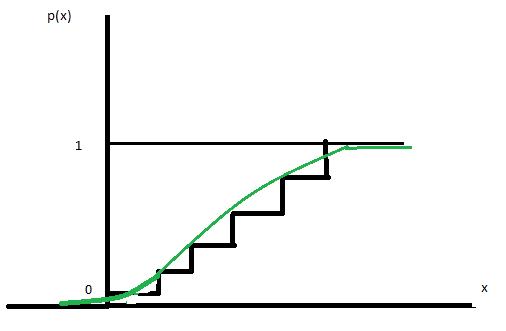
Графическое представление функций:

2.2.7.Основные законы распределения вероятности появления непрерывных результатов измерения:

1.Нормальный закон распределения (закон Гаусса).

ЦПТ

Непрерывная случайная величина X имеет нормальный закон распределения с параметрами a и 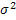, если ее плотность вероятности имеет вид:

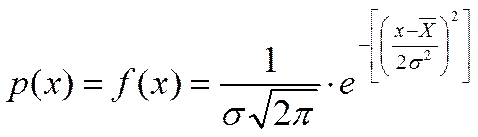
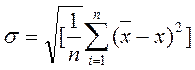
Обозначение: .

Математическое ожидание: .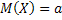

Дисперсия: .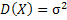

Нормальный закон распределения с параметрами X= 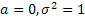, т.е. N(0;1), называется стандартным или нормированным.

Функция распределения нормально распределенной случайной величины имеет вид:

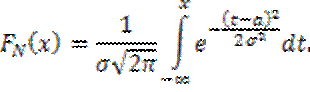
Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервале [x₁, x₂], равна

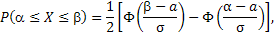
где 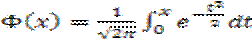– функция Лапласа.

Вероятность попадания случайной величины в интервал, симметричный относительно центра рассеяния а:

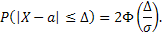
Если 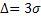, то 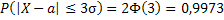. Отсюда следует правило «трех сигм»: если 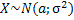, то практически достоверно, что значения случайной величины Х заключены в интервале .

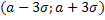Нормальный закон распределения занимает центральное место в теории и практике вероятностно-статистических методов. Он является предельным законом, к которому приближаются многие другие законы распределения. Центральная предельная теорема теории вероятностей утверждает, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному.

Моделирование нормально
распределенных случайных величин http://stratum.ac.ru/textbooks/modelir/lection24.html

Нормальный закон распределения встречается в природе весьма часто, поэтому для него разработаны отдельные эффективные методы моделирования. Формула распределения вероятности значений случайной величины x по нормальному закону имеет вид:

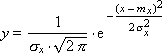
Как видно, нормальное распределение имеет два параметра: математическое ожидание m_x и среднеквадратичное отклонение σ_x величины x от этого математического ожидания.

x — случайная величина; y(x) — вероятность принятия случайной величиной значения x; mx — математическое ожидание; σx — среднее квадратичное отклонение.

Нормализованным нормальным распределением называется такое нормальное распределение, у которого m_x = 0 и σ_x = 1. Из нормализованного распределения можно получить любое другое нормальное распределение с заданными m_x и σ_x по формуле: z = m_x + x · σ_x.

Рассматривая последнюю формулу, вспомните формулы компьютерной графики: операция масштабирования выражается в математической модели через умножение (это соответствует изменению разброса величины, растягиванию геометрического образа), операция смещения выражается через сложение (это соответствует изменению значения наиболее вероятной величины, смещению геометрического образа).

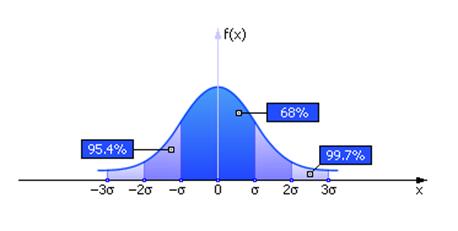
Функция нормального распределения имеет вид колокола. На рис. 25.1 показано нормализованное нормальное распределение.

Рис. 25.1. Графический вид нормального закона распределения случайной величины х с параметрами mx = 0 и σx = 1 (распределение нормализовано)

График на рис. 25.1 показывает, что в области –σ < x < σ на графике сосредоточено 68% площади распределения, в области –2σ < x < 2σ на графике сосредоточено 95.4% площади распределения, в области –3σ < x < 3σ на графике сосредоточено 99.7% площади распределения («правило трех сигм»). Вспомните, пожалуйста, рис. 2.7 из лекции 02.

Пример. По нормальному распределению распределен рост людей, находящихся одновременно в большой аудитории. А именно: достаточно мало людей очень большого роста, и столь же мала вероятность встретить людей очень малого роста. В основном, легче встретить людей среднего роста — и вероятность этого велика.

Например, средний рост людей составляет, в основном, 170 см, то есть m_x = 170. Известно также, что σ_x = 20. На рис. 25.1 показано, что доля людей с ростом от 150 до 190 (170 – 20 < 170 < 170 + 20) составляет в обществе 68%. Доля людей от 130 см до 210 см (170 – 2 · 20 < 170 < 170 + 2 · 20) составляет в обществе 95.4%. Доля людей от 110 см до 230 (170 – 3 · 20 < 170 < 170 + 3 · 20) составляет в обществе 99.7%. Например, вероятность того, что человек окажется ростом меньше 110 см или больше 230 см составляет всего 3 человека на 1000.