Составьте таблицу истинности для формулы:

М.В. Ломоносов

Логика (от древнегреческого logos – слово, выражающее мысль) является началом любой научной теории. Логика как наука о способах мышления, приводящих к истине, возникла в глубокой древности.

Начало науки о законах и формах мышления связывают с именем Аристотеля. Именно Аристотель (384–322 гг. до н.э.) создал чистую систему силлогизмов – правил вывода, что и привело к возникновению теории логики. Математическое исследование этих вопросов берет свое начало от основополагающего труда Джорджа Буля, изданного в Лондоне в 1854 году. Этот труд Буля положил начало математической логики, систематическое развитие которой было достигнуто работами многих математиков XX века.

Правила вывода позволяют преобразовывать исходные утверждения подобно тому, как тождественные преобразования в математике дают возможность решать различные системы уравнений. Следующим шагом формализации логики является появление специальной символики для точной и компактной записи утверждений и определения операций над ними.

Идея перенесения тех методов, которые обычно применяются в математике, на логику была реализована Б. Паскалем (1646-1716), Г. Лейбницем (1646-1716), Дж. Булем (1815-1864), О. Де Морганом (1806-1871), Г. Фреге (1848-1925), Б. Расселом (1872-1970), Д. Гильбертом (1862-1943), А. Марковым (1903-1979) и др. Так появился язык логики как логическое продолжение языка математики.

С появлением языка математической логики стало возможным составлять алгоритмы логического вывода. Стали вести речь о создании «искусственного интеллекта». В последнее время логика находит все более широкое применение в технике при исследовании и разработке вычислительных машин, дискретных автоматов. Ее методы используются в теории преобразования и передачи информации, теории вероятностей и комбинаторном анализе. Математическая логика находит свое применение в экономике, биологии, медицине, психологии, праве, языкознании.

Сложившийся стереотип о том, что математическая логика – наука, изучающая законы мышления с применением аппарата математики, главным образом, для нужд самой математики, в современных условиях меняется коренным образом. С расширением области применения и дальнейшим развитием математической логики изменяется и взгляд на нее. Объектами математической логики являются любые дискретные конечные системы, а ее главная задача – структурное моделирование таких систем.

В ходе изучения темы « Элементы математической логики» студент должен:

1. знать основные понятия математической логики, такие как: высказывание, свойства высказывания (закон исключения третьего, закон противоречия), предикат, кванторы общности и существования, алгебра высказываний (операции над высказываниями), основные свойства операций над высказываниями, истинностные таблицы,тавтология.

2. уметь доказывать и объяснять некоторые свойства операций над высказываниями; выполнять алгебраические операции над высказываниями (строить таблицы истинности алгебраических операций над высказываниями); решать задачи типа:

1. Прочтите словами следующие высказывания, записанные знаками;
5 > 3, 10 + 2 = 14, 4 – 1 < 7, 4⁴ = 256, 5³ ¹ 125
Какие из этих высказываний истинные, какие ложные?

2. Рассмотрите следующие два высказывания:
С º {существуют четные простые числа}
H º {существуют нечетные простые числа}
Определите их истинность. Является ли высказывание H отрицанием высказывания С? Составьте отрицания к обоим высказываниям.

3. Составьте таблицу истинности для формулы: .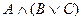

4. Докажите следующее равенство: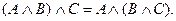

5. Проверьте, задает ли следующая формула тавтологию: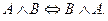

6. Запишите с помощью знаков ", $ следующие высказывания:
1. Каково бы ни было натуральное число x, найдется такое натуральное число y, что (x+y) – простое число.
2. Каково бы ни было натуральное число y, среди натуральных чисел найдется такое число x, что (x+y) – четное число.
3. Каково бы ни было натуральное число x, можно подобрать такое натуральное число y, что x² +y² < 100.

Примерный вариант решения задач.

1. Прочтите словами следующие высказывания, записанные знаками;
5 > 3, 10 + 2 = 14, 4 – 1 < 7, 4⁴ = 256, 5³ ¹ 125
Какие из этих высказываний истинны, какие ложны?

Решение: Пять больше трех. И
Сумма чисел 10 и 2 равна 14. Л
Разность чисел 4 и 1 меньше 7. И
Четыре в четвертой степени равно 256. И
Пять в кубе неравно 125. Л

Рассмотрите следующие два высказывания: С º {существуют четные простые числа} H º {существуют нечетные простые числа} Определите их истинность. Является ли высказывание H отрицанием высказывания С? Составьте отрицания к обоим высказываниям.

Решение:
По определению, число является простым, если имеет только два делителя (т.е. 1 и само себя).

Определим истинность высказываний: высказывание С – истинное (т.к. число 2 – четное и простое), высказывание Н – истинное (например, число 7 – нечетное и простое).
Высказывание Н не является отрицанием высказывания С (т.к. оба истинны).
Составим отрицания данных высказываний:
С º {не существуют четные простые числа},
H º {не существуют нечетные простые числа}.

Составьте таблицу истинности для формулы: .

Решение:

А	В	С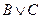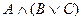

4. Докажите следующее равенство: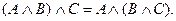

Решение:

А	В	С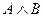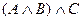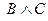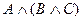

Сравнивая выделенные колонки, заключаем: равенство доказано.

5. Проверьте, задает ли следующая формула тавтологию: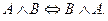

Решение:

А	В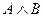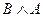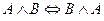

Таким образом, 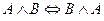–тавтология.

6. Запишите с помощью знаков ", $ следующие высказывания:
1. Каково бы ни было натуральное число x, найдется такое натуральное число y, что (x+y) – простое число.
2. Каково бы ни было натуральное число y, среди натуральных чисел найдется такое число x, что (x+y) – четное число.
3. Каково бы ни было натуральное число x, можно подобрать такое натуральное число y, что x² +y² < 100.

Решение: 1. .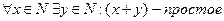
2. .
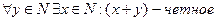3.

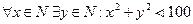
Глоссарий по теме «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ»

Высказывание – повествовательное предложение, относительно которого имеет смысл говорить, что его содержание истинно или ложно. Принято обозначать высказывания большимим латинскими буквами, например А, В, С и т.д. Истинные высказывания принято обозначать с помощью символа И или цифры 1, ложные – с помощью Л или цифры 0.

Двойное отрицание – пусть А – произвольное высказывание. Его отрицание А также является высказыванием. Значит можно рассматривать и его отрицание, т.е. высказывание А. Оно называется двойным отрицанием высказывания А. Его можно сформулировать словами так: утверждение о том, что высказывание А не выполняется места не имеет. По смыслу это совпадает с самим высказыванием А.

Дизъюнкция – логическое «или».В математике часто используется операция дизъюнкция, обозначается символом , читается «или». В математической логике операция не имеет разделительного смысла, т.е. А В означает, что либо имеет место А (но не В), либо имеет место В (но не А), либо же (и в этом отличие) имеют место А и В вместе.

Закон исключения третьего – всякое высказывание является либо истинным, либо ложным.

Закон отрицания отрицания – двойное отрицание А истинно в том и только в том случае, если истинно само высказывание А(т.е. если А истинно, то и А истинно, а если А ложно, то и А ложно).

Закон противоречия – никакое высказывание не может быть одновременно истинным и ложным.

Импликация– Пусть А и В – два элементарных высказывания. Импликацией данных высказываний называется высказывание «Если А, то В» и обозначается А Þ В.

Кванторы – кванторы (общности, существования) превращают предикат в высказывание. Причем, квантор общности 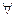из словесных формулировок заменяет слова: всякий, каждый, любой, все. Квантор существования $ из словесных формулировок заменяет слова: существует, найдется, какой-нибудь, хотя бы один.

Конъюнкция –логическое «и». В математике одновременное выполнение двух свойств принято называть конъюнкцией этих свойств и обозначать знаком (читается «и»).

Множество истинности предиката – если задано некоторое универсальное множество U, на котором определен предикат B(x), то с точки зрения теории множеств это означает, что выделено некоторое подмножество В Ì U, состоящее из всех x Î U, при подстановке которых B(x) превращается в истинное высказывание. Его дополнение сВ состоит из всех x Î U, при подстановке которых B(x) превращается в ложное высказывание. Множество В называется множеством истинности предиката B(x).

Отрицание– логическая операция, которая позволяет из всякого высказывания А получить новое высказывание, отрицая его, т.е. утверждая, что высказывание А не имеет места, не выполняется. Отрицание высказывания А обозначается символом А.Запись А читается как «отрицание высказывания А» или «не А».

Предикат (неопределенное высказывание) – предложение A(n), которое при каждом конкретном n превращается в некоторое высказывание.

Равносильные (эквивалентные) высказывания – два составных высказывания А и В называют равносильными (эквивалентными) , если они одновременно истинны или одновременно ложны при любых предположениях об истинности входящих в них элементарных высказываний. Записывают: А = В.

Составное (сложное) высказывание – высказывание, которое можно расчленить на другие высказывания.

Тавтология – составное высказывание, истинное при любых предположениях о входящих в него элементарных высказываниях.

Эквиваленция – Пусть А и В – два элементарных высказывания. Эквиваленцией данных высказываний называется высказывание «А тогда и только тогда, когда В» и обозначается А Û В.

Элементарное высказывание – если никакая часть высказывания сама уже не является высказыванием (или по крайней мере не рассматривается как таковое).

УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Является ли высказыванием утверждение «У любой собаки четыре глаза»?

2. Найдите множество истинности высказывания: сумму в n рублей можно уплатить купюрами в 50 и 100 рублей.

3. Используя кванторы, запишите высказывание: «Уравнение ax = b имеет решение». Найдите множество истиности этого высказывания.

4. Используя кванторы, запишите высказывание: «Уравнение ax = b имеет положительный корень». Найдите множество истиности этого высказывания.

5. Используя кванторы, запишите высказывание: «Существует целое число, которое делится на любое другое целое число, отличное от нуля». Истинно ли это высказывание?

1. Постройте отрицание высказывания: «Каждому овощу свое время».
2. Постройте отрицание высказывания: «Среди ста трехзначных чисел найдутся два равных». Какое из этих высказываний истинно?
3. Постройте отрицание высказывания: «Не существует ромба, который может быть вписан в окружность». Какое из этих высказываний истинно?
4. Постройте отрицание высказывания: «Во всяком треугольнике медианы пересекаются в одной точке». Какое из этих высказываний истинно?
5. Что можно сказать об истинности высказывания ( А В С) А, если А – ложное высказывание, а В и С – истинные?
6. Пусть А – истинное высказывание, а В и С – ложные. Будет ли истинным высказывание (А В) ( В С) ( С А)? ( В А) ( С А)?
7. При каком условии высказывания А (В С) и ( А С) (А В) одновременно истинны или ложны?

13. Составьте таблицу истинности для формулы:
13.1. А (В С),
13.2. А (В С).

14. Докажите следующее равенство (для всех значений А и В):
14.1. (А В) С = А (В С),
14.2. (А В) С = (А С) (В С),
14.3. (А С) ( В С) = (А В) С.

15. Покажите, что высказывания А и (А В) (А В) всегда одновременно истинны или ложны.

16. Пусть А – высказывание: «число делится на 2», В – «число делится на 7», С – «число делится на 14». Какие из следующих высказываний истинные:
16.1. С Þ А В,
16.2. А В Þ С,
16.3. С В Þ А?

17 Составьте таблицу истинности для формулы:
17.1. А (В Þ С),
17.2. А (В Þ С),
17.3. А ( В Þ С).

18. Докажите следующее равенство:
18.1. (А Þ В) = ( А В),
18.2. (А Þ В) = ( В Þ А).

19. Даны следующие высказывания: А º {Сегодня суббота}, В º {Сегодня пасмурно}, С º {Я буду читать книгу}. Определите их истинность. Составьте таблицу истинности для указанных формул и определите их истинность:
19.1. С Þ (А В),
19.2. С Þ (А В),
19.3. С Þ (А В).

20. Докажите следующую тавтологию:
20.1. А В Û В А.
20.2. А В Û В А.
20.3. (А В) Û В А.
20.4. ((А В) А) В.
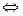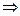20.5. (А В) Û А В.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО ТЕМЕ «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ»

1. Математическая логика: понятие, история развития.

2. Высказывания.

3. Предикаты.

4. Квантор общности.

5. Квантор существования.

6. Логические операции: отрицание.

7. Логические операции: конъюнкция.

8. Логические операции: дизъюнкция.

9. Логические операции: импликация.

10. Логические операции: эквиваленция.

СПИСОК ЛИТЕРАТУРЫ

1. Грес П.В. Математика для гуманитариев: Уч. пособие / П.В. Грес. – М.: Юрайт, 2000. – 112 с.

2. Болтянский В.Г., Савин А.П. Беседы о математике. Книга 1. Дискретные объекты. – М.: ФИМА, МЦНМО, 2002. – 368 с.

3. Болтянский В.Г., Савин А.П. Беседы о математике. Книга 1. Дискретные объекты. – М.: ФИМА, МЦНМО, 2002. – 368 с.

4. Курс математики (для гуманитарных специальностей вузов): Учебно-методическое пособие / ЧГАКИ. – Челябинск, 200. – 45 с.

5. Болтянский В.Г., Сидоров Ю.В., Шабунин М.И., Мордкович А.Г.: Учебное пособие. Математика. Лекции, задачи, решения. – Альфа. – 640 с.