Полное сопротивление в цепи переменного тока. Резонанс напряжений

Представим цепь, в которой последовательно соединены резистор, катушка индуктивности и конденсатор (рис. 14.7, а). Напряжение на зажимах a, b цепи, создаваемое внешним источником, выражается зависимостью (14.18). Как было показано в § 14.2, в общем случае сила тока в цепи и напряжение изменяются не в од­ной фазе, поэтому

I = I_m cos (wt - j), (14.34)

где j — разность фаз напряжения и силы тока.

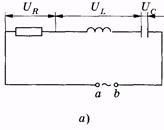
` Рис. 14.7

Сумма напряжений на отдельных участках равна внешнему напряжению:

U = U_m cos wt =U_R + U_L + U_C. (14.35)

В соответствии с изложенным в § 14.2, напряжения U_R, U_L и U_{C c} можно записать так:

U_R = U_m cos (wt - j) (14.36)

(в фазе с током);

U_I = U_Lm cos (wt - j + p/2) (14.37)

(опережает силу тока по фазе на p/2);

U_C = U_Cm cos (wt - j - p/2) (14.38)

(отстает от силы тока по фазе на p/2).

Подставив (14.36) — (14.38) в (14.35), после тригонометрических преобразований можно получить выражение для полного сопротив­ления цепи переменного тока и разности фаз ф. Однако более просто и наглядно удается это сделать с помощью векторных диаграмм.

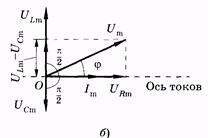
На рис. 14.7, б по оси токов направлен вектор амплитуды силы тока I_m. Так как по всей цепи амплитуда силы тока одинакова, то амплитуды напряжений на участках отложим относительно этого вектора: вектор U_Rm — в одной фазе с силой тока; вектор U_Lm - с опережением силы тока по фазе на p/2, вектор U_Cm— c отставанием от силы тока по фазе на p/2. Суммируя три вектора, находим графически значения U_mи j. Используя теорему Пифагора, имеем

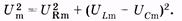(14.39)

Подставляя в (14.39) выражения этих амплитуд из (14.21), (14.27) и (14.32) и учитывая закон Ома, находим

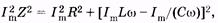(14.40)

где Z — полное сопротивление цепи переменного тока, называемое импедансом. Из (14.40) получаем

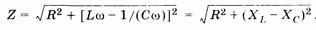(14.41)

Омическое сопротивление R цепи называют также активным, оно обусловливает выделение теплоты в цепи в соответствии с законом Джоуля—Ленца. Разность индуктивного и емкостного сопротивлений (X_L – Х_С) называют реактивным сопротивлением. Оно не вызывает нагревания элементов электрической цепи.

Запишем закон Ома применительно к амплитудам напряже­ния и силы тока в цепи (рис. 14.7):

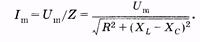(14.42)

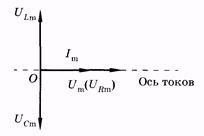
Рис. 14.8 Из рис. 14.8 выразим также и значение j через известные величины:

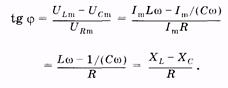(14.43)

Если индуктивное и емкостное сопротивления цепи при их последовательном соединении одинаковы (Х_L = Х_C), то [см. (14.41)] Z = R, и из (14.43) имеем tg j = 0 и j = 0. Это означает, что сила тока и приложенное напряжение изменяются в одной фазе так, как будто в цепи имеется только омическое сопротивление; напряжения на индуктивности и емкости одинаковы по амплитуде, но противоположны по фазе.

Этот случай вынужденных электрических колебаний называют резонансом напряжения.

Так как U_Lm = U_Cm, то Lw_рез = 1/(Сw_рез). Отсюда находим резо­нансную частоту:

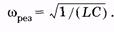(14.44)

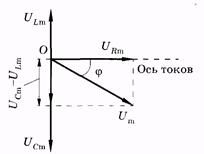При этом условии полное сопротивление Z цепи имеет на­именьшее значение, равное R, а сила тока достигает наибольшего значения. Векторная диаграмма для резонанса напряжений в цепи показана на рис. 14.8.

Если Lw > 1/(Сw), то tg j > 0 и j > 0, сила тока отстает по фазе от приложенного напряжения (см. рис. 14.7, б). При Lw < 1/(Сw) имеем tg j < 0 и j < 0. Сила тока опережает по фазе напряжение. Векторная диаграмма для этого случая дана на рис. 14.9.

Рис. 14.9