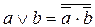Представление информации физическими сигналами

Логические функции и логические элементы.

Основные понятия

Все цифровые вычислительные устройства построены на элементах, которые выполняют те или иные логические операции.

Для формального описания логической стороны процессов в цифровых устройствах используется алгебра логики (АЛ).

АЛ имеет дело с логическими переменными, которые могут принимать только два значения (ИСТИНА и ЛОЖЬ, TRUE и FALSE, ДА и НЕТ, 1 и 0). Наиболее распространено последнее обозначение. При этом 1 и 0 нельзя трактовать как числа, над ними нельзя производить арифметические действия.

Логические переменные хорошо описывают состояния таких объектов, как реле, тумблеры, кнопки ., т.е. объектов, которые могут находиться в двух четко различимых состояниях: включено - выключено. К таким объектам относятся и полупроводниковые логические элементы, на выходе которых может быть лишь одиниз двух четко различимых уровней напряжения. Чаще более высокий, или просто ВЫСОКИЙ (HIGH) уровень принимается за логическую единицу, а более низкий, или просто НИЗКИЙ (LOW),- за логический нуль.

Представление информации физическими сигналами.

Как уже говорилось, физическими аналогами логических переменных "0" и "1" служат сигналы, способные принимать два хорошо различимых состояния, например, потенциал низкого и высокого уровней, разомкнутое и замкнутое состояние контакта реле и т.п.

В схемах цифровых устройств (ЦУ) переменные и соответствующие им сигналы изменяются не непрерывно, а лишь в дискретные моменты, обозначаемые целыми неотрицательными числами: 0,1,2,.. i… Временной интервал между двумя соседними моментами дискретного времени называется тактом. Обычно ЦУ содержат специальный блок, вырабатывающий синхронизирующие сигналы, отмечающие моменты дискретного времени (границы тактов).

В современных ЦУ применяется потенциальный способ представления информации. Потенциальный сигнал сохраняет постоянный уровень в течение такта, а его значение в переходные моменты не является определенным (рис. 1.1)

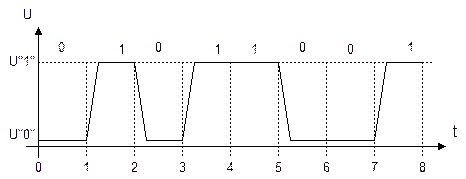
Рис. 1.1. Представление цифровой информации сигналами потенциального типа (последовательный код).

Слово информации может быть представлено последовательным или параллельным кодом.

При последовательном коде каждый временной такт предназначен для отображения одного разряда кода слова (рис. 1.1). В этом случае все разряды слова фиксируются по очереди одним и тем же элементом и проходят через одну линию передачи информации.

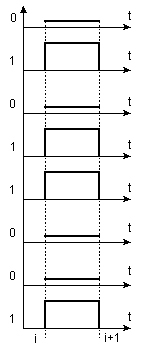
При параллельном коде все разряды двоичного слова представляются в одном временном такте, фиксируются отдельными элементами и проходят через отдельные линии, каждая из которых служит для представления и передачи только одного разряда слова. Код слова развертывается не во времени, а в пространстве, т.к. значения всех разрядов слова передаются по нескольким линиям одновременно (рис. 1.2).

Рис. 1.2. Представление информации параллельным кодом.

Логические функции.

Функции АЛ принимают значения 1 или 0 в зависимости от значений своих аргументов. Одна из форм задания логической функции - табличная. Таблицы, отображающие соответствие всех возможных комбинаций значений двоичных аргументов значениям логической функции, называют таблицами истинности.

Как бы ни была сложна логическая связь между логической функцией и ее аргументами, эту связь всегда можно представить в виде совокупности трех простейших логических операций: НЕ, И, ИЛИ. Этот набор называют булевским базисом, в честь английского математика Д.Буля (1815-1864), разработавшего основные положения АЛ.

Функция НЕ (другие названия: отрицание, инверсия) - это функция одного аргумента. Она равна 1, когда ее аргумент равен 0, и наоборот. Обычное обозначение Q= 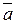. Встречаются и другие обозначения Q=НЕ 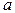, Q= 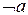. Читается «Q есть не а».

Электронный логический элемент (ЛЭ), реализующий функцию НЕ в виде определенных уровней напряжения, называют инвертором. Инвертор на схемах изображается, как показано на рис. 1.3,а. Вход- слева, выход- справа, кружок- символ инверсии. Условное изображение инвертора (или любого другого ЛЭ) на схеме может быть повернуто на 90° (вход- сверху, выход- снизу, рис. 1.3,б). Другие углы поворота и направления входов и выходов не допускаются.

В релейно-контактной технике функцию НЕ реализует нормально замкнутый контакт (рис. 1.3,в), т.е. такой контакт реле, который замкнут, пока в обмотке нет токового сигнала 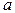, и размыкается при подаче тока .

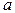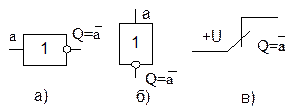
Рис.1.3. Инвертор

а) предпочтительное изображение

б) допустимое изображение

в) реализация НЕ в релейно-контактной технике

Функция И (другие названия: конъюнкция, логическое умножение, AND)- это функция двух или большего числа аргументов.

Обозначение: Q=a&b; Q=aÙb; Q=a×b; Q=ab. Читается «Q есть a и b».

Функция И равна 1 тогда и только тогда, когда все ее аргументы равны 1. В релейно-контактной технике функция И реализуется последовательным включением нормально разомкнутых контактов (рис. 1.4,а). Ток в цепи пойдет, когда контакты замкнуты, т.е. находятся в единичном состоянии.

Значения функции И для всех комбинаций аргументов a и b приведены в таблице 1.1. Там же приведены значения и других часто используемых функций, о которых речь будет вестись ниже.

Элемент, реализующий функцию И, называют элемент И или конъюнктор. Элемент И часто используют для управления потоком информации. При этом на один его вход поступают логические сигналы, несущие некоторую информацию, а на другой- управляющий сигнал: пропускать- 1, не пропускать-0. Элемент И, используемый таким образом, называют вентиль (gate).

Таблица 1.1

Аргументы	Функции
а	b	И	ИЛИ	И-НЕ	ИЛИ-НЕ	М2	º

Функцию И можно построить от любого числа аргументов. На рис. 1.2,б и в показаны условные изображения двух- и четырехвходового конъюнкторов.

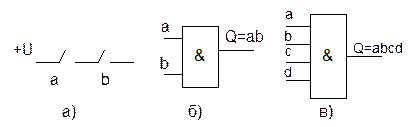
Рис. 1.4. Конъюнктор

а) реализация операции И на контактах реле

б) условное изображение двухвходового конъюнктора 2И (AND2)

в) то же для четырехвходового- 4И (AND4)

Функция ИЛИ (другие названия: дизъюнкция, логическое сложение, OR)- это функция двух или большего числа аргументов. Функция ИЛИ равна 1, если хотя бы один из ее аргументов равен 1. Обозначение: Q=aÚ b, Q=a+b. Читается: «Q есть a или b». Использовать знак «плюс» можно в тех случаях, когда дизъюнкцию нельзя смешать с арифметическим суммированием и сложением по модулю 2.

Условное изображение трехвходового дизъюнктора (3ИЛИ, OR3) показано на рис. 1.5,а. В релейно-контактных схем ах функция ИЛИ реализуется параллельным включением контактов (рис. 1.5,б)

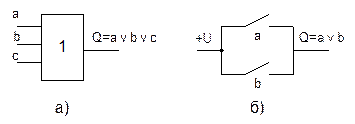
Рис. 1.5. Дизъюнктор

а) условное изображение

б) реализация ИЛИ на контактах

Законы алгебры логики

АЛ базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с логическими переменными. Каждая аксиома представлена в двух видах, что вытекает из принципа дуальности логических операций, согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять 1 на 0, 0 на 1, знак Ú на ×, а знак × на Ú.

Аксиомы операции отрицания: , .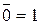

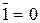Аксиомы операций конъюнкции и дизъюнкции:

1а) 0×0=0 1б) 1Ú1=1

2а) 1×0=0×1=0 2б) 0Ú1=1Ú0=1

3а) 1×1=1 3б) 0Ú0=0

Законы АЛ вытекают из аксиом и также имеют две формы выражения а) и б).

1. Переместительный закон

а) a×b=b×a б) aÚb=bÚa

2. Сочетательный закон

а) a(bc)=(ab)c=abc б) aÚ(bÚc)=(aÚb)Úc=aÚbÚc

3. Закон тавтологии

а) a×a=a б) aÚa=a

4. Закон обращения: если a=b, то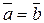

5. Закон двойной инверсии: 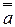=a

6. Закон нулевого множества

а) a×0=0 б) aÚ0=a

7. Закон универсальногомножества

а) a×1=a б) aÚ1=1

8. Закон дополнительности

а) a× 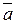=0 б) aÚ 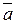=1

9. Распределительный закон

а) a(bÚc)=ab+aс б) aÚ(bc)=(aÚb)( aÚc)

10. Закон поглощения

а) aÚab=a б) a(aÚb)=a

11. Закон склеивания

а) (aÚb)(aÚ 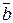)=a б) a.bÚ 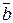a. =a

12. Закон инверсии (закон Де Моргана)

а) 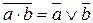б)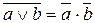

или после инвертирования

в) 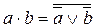г)