Слабая и сильная аксиома выявленных предпочтений

Теория выявленных предпочтений является логическим продолжением теории потребительского поведения и теории отношения предпочтения–безразличия.

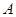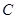На рис. 5.1. представлена исходная бюджетная линия и набор , приобретаемый потребителем. Он предпочитает его наборам и . Потребитель прямо выявлено предпочитает набор 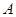набору , 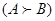. Цена на товар 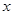снизилась, а на товар 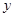выросла так, что бюджетная линия заняла положение 2. При таком бюджетном ограничении набор 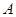стал недоступен. Теперь

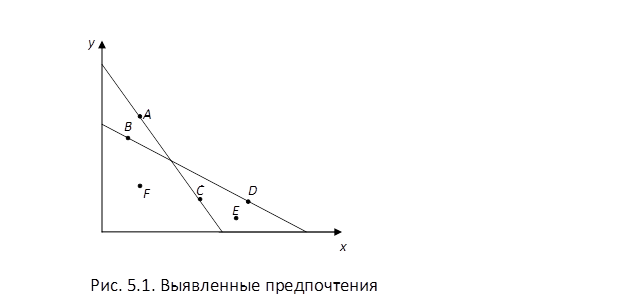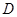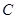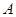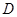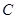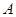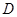потребитель приобретает какой-либо другой набор, например, набор . Этот набор прямо выявлено предпочитается наборам и . Но так как набор предпочитается набору , а набор предпочитается наборам и , то набор не прямо, а косвенно через набор , предпочитается наборам и .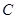

Теория выявленных предпочтений строится на следующих предпосылках (аксиомах).

Потребитель, приобретая товары и услуги, обязательно тратит весь свой доход .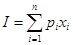

Выбор потребителя является единственным. Если набор выбран, то он определяет рыночную ситуацию единственным образом с точностью до положительного множителя так, что .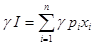

Потребительский набор 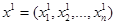прямо выявлено, т.е. явно, предпочитается набору 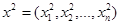, если 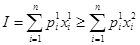. Данное соотношение иллюстрируется наборам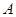и , и 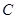, а также , 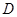и 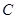. Прямое выявленное предпочтение набора 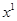набору 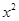означает, что из двух наборов потребитель выбрал 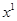, а набор 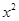не выбрал. Потребитель выбрал самый дорогой набор. Прямое выявленное предпочтение одного набора другому осуществляется в одной и той же рыночной ситуации, т.е. при одних и тех же доходе и ценах.

1. Отношение прямого выявленного предпочтения не обладает свойством транзитивности. Так, если набор 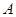прямо выявлено предпочитается набору и не предпочитается набору 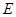, то, несмотря на то, что набор прямо выявлено предпочитается набору 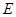, набор 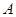прямо выявлено не предпочитается набору .

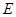2. Потребительский набор 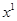косвенно выявлено предпочитается набору 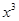, если 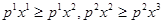и если потребительский набор 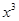не принадлежит бюджетному множеству, соответствующему рыночной ситуации .

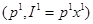Однако, разделив выявленное предпочтение на прямое и косвенное, сохраняется неясность относительно того, принадлежит ли набор 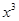бюджетному множеству, соответствующему рыночной ситуации 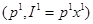, или не принадлежит. На рис. 5.1. речь идет о наборах 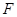и 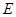. В последующем независимо от того, принадлежит ли набор 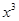бюджетному множеству, соответствующему рыночной ситуации 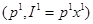, или не принадлежит, используется терминология: набор 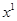выявлено предпочитается набору 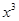, если .

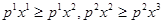В теории выявленных предпочтений нет функции полезности и нет кривых (поверхностей) безразличия. По результатам наблюдений за поведением потребителя на рынке можно дать оценку кривой (поверхности) безразличия. Если известно, что при ценах 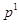потребитель выбрал набор 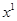(на рис. 4.1. набор 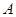), а при ценах 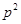- набор 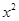(на рис. 5.1. набор 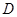), то кривая безразличия будет располагаться выше верхней части первой и нижней части второй бюджетных линий, касаясь первой бюджетной линии в точке 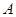, поскольку этот набор был выбран. Если при изменении цен увеличивается число наблюдений и точек, отмечающих наборы, которые предпочитает всякий раз потребитель, то можно выделить область на плоскости, ограниченную бюджетными линиями, в которой находится кривая безразличия и убедиться в том, что она выпукла относительно начала координат. Студенту рекомендуется самостоятельно построить четыре бюджетных линии, выбрать предпочтительные наборы на каждой из них так, чтобы каждый последующий набор был предпочтительнее предыдущего, и убедиться в выпуклости кривой безразличия.

Слабая аксиома выявленных предпочтений характеризует прямо выявленное предпочтение. Если потребитель прямо выявлено предпочитает набор 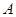набору , то он не может в то же время прямо выявлено предпочитать набор набору 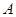. На рис. 5.1. набор 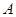прямо выявлено предпочитается набору . Но после изменения цен потребитель выбирает набор не потому, что он предпочитает его набору 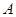, а потому, что при новом бюджетном ограничении набор 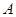ему не доступен. Аналитически ситуацию можно представить так.

Если 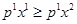, то 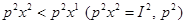- рыночная ситуация, соответствующая набору 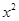, если он был выбран. Неравенство 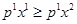означает, что потребителю доступны оба набора 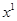и 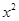, но потребитель выбрал 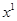. Неравенство 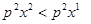означает, что при ценах 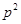потребитель выбрал набор 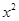, а набор 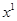потребителю был недоступен.

Рассмотрим ситуацию, когда потребитель на первой бюджетной линии первоначально выбрал набор 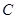(рис. 5.2.) и выявлено предпочел его набору . После изменения цен бюджетная линия перемещается в положение второй линии и тогда потребитель выбирает набор . Новое бюджетное ограничение позволяет ему купить 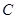, но он выбирает .Таким образом, на первой линии 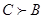, на второй - 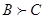. Слабая аксиома выявленных предпочтений нарушается.

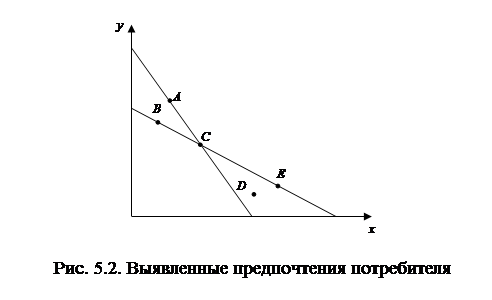
Нарушение имеет место в случаях.

1. Покупая набор , потребитель поступил нерационально. Полезность набора 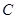была выше, чем полезность .

2. Потребитель поступил нерационально, приобретая набор 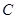. Полезность набора была выше.

3. Вместе с изменениями цен и бюджетного ограничения изменились вкусы и предпочтения потребителя, изменилась его оценка наборов и .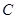

Если выявленные предпочтения обладают свойством симметричности, т.е. 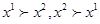, то слабая аксиома выявленных предпочтений не выполняется.

Учитывая возможные нарушения, слабую аксиому выявленных предпочтений можно сформулировать таким образом: если поведение потребителя рационально, его вкусы не изменяются и он покупает набор 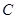, хотя мог бы купить набор , то как бы ни изменялись цены и доход, потребитель не купит набор , если ему доступен набор 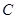. В короткие периоды времени вкусы потребителей практически не изменяются, а цены и доход являются динамичными переменными.

Наблюдения за поведением потребителя на рынке, т.е. за тем, сколько товаров и по каким ценам покупает потребитель, позволяют сделать вывод о соответствии или несоответствии поведения потребителя слабой аксиоме выявленных предпочтений. Допустим, потребитель приобретает два товара 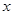и 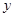в различном сочетании по изменяющимся ценам. Результаты наблюдений представим в нижеследующей таблице 1.

Таблица 1. Цены на товары и выбираемые потребительские наборы.

Номер наблюдения	Цены	Выбираемые потребительские наборы
.
.

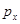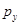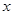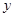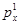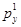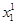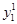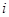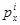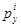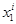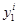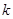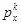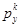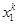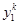По рыночным ценам потребитель приобретает наборы. Расходы потребителя на покупку всех наборов в ценах первого наблюдения составляют 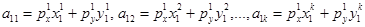. Расход потребителя при покупке 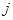-го набора в ценах 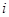-го наблюдения равен 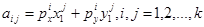. Элементы 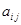образуют квадратную матрицу.

.

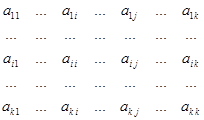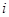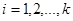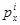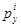Элементы -ой строки, , матрицы показывают последовательно все расходы потребителя, которые он имел бы, если бы по ценам и приобретал бы наборы 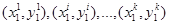. В действительности потребитель приобрел набор 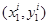. Элементы главной диагонали матрицы показывают реальные расходы потребителя, который приобретал наборы 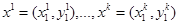по ценам 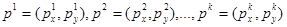. Остальные элементы матрицы показывают гипотетические расходы потребителя, которые он имел бы, приобретая наборы с индексом 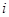по ценам с индексом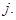

Если 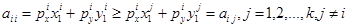, то это означает, что набор 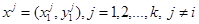доступен потребителю, но он предпочел набор 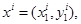и этот набор выявлено предпочитается набору .

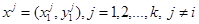Если 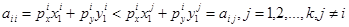, то это означает, что набор 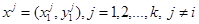был недоступен потребителю, когда он приобретал набор 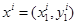. В таком случае нельзя определить, какой набор предпочтительнее другого.

Матрицу расходов потребителя используем для выяснения наличия или отсутствия нарушений слабой аксиомы выявленных предпочтений. Если в матрице наборы и соответствующие им расходы 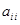предпочитались 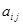и 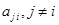, то для потребительских наборов с расходам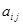и и 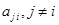слабая аксиома выявленных предпочтений не выполняется. Наличие выявленных предпочтений, для которых одновременно выполняются условия 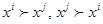,означает, что для этих наборов слабая аксиома выявленных предпочтений не выполняется.

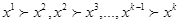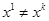Сильная аксиома выявленных предпочтений утверждает, что если и , то 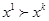, и не выполняется 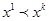. Или в другой форме 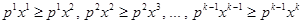. Сильная аксиома выявленных предпочтений включает слабую аксиому (при ).

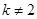С помощью матрицы расходов потребителя можно определить, выполняется или не выполняется сильная аксиома выявленных предпочтений. Следует помнить, что по результатам наблюдений за поведением потребителя на рынке можно получить выводы, не совместимые с основными положениями теории потребительского поведения. Тем более такие выводы можно получить, если используются, вместо реальных, гипотетические данные.

До сих пор явно или неявно предполагалось, что в случае двух товаров в наборе кривая безразличия выпукла относительно начала координат, а бюджетная линия касается ее только в одной точке. Если в наборе содержится 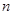товаров, то речь идет о строгой выпуклости предпочтений потребителя. Если в качестве условия использовать предпосылку о выпуклости предпочтений потребителя (а не строгой выпуклости), то от слабой аксиомы можно перейти к обобщенной аксиоме выявленных предпочтений. Она формулируется следующим образом. Если набор прямо или косвенно предпочитается другому набору 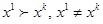, то не выполняется предпочтение .

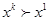Без доказательства приводится теорема Эфриата. Чтобы наблюдения о потребительском поведении соответствовали обобщенной аксиоме выявленных предпочтений необходимо и достаточно, чтобы основой потребительского поведения являлись рациональные предпочтения.

5.2.Динамика дохода, цен и благосостояние потребителей

В анализе динамики благосостояния потребителя используются индексы цен, дохода и объемов приобретаемых товаров и услуг. В базисном периоде их величины имеют индекс 0, в текущем периоде - 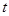. Если текущим периодом является следующий за базисным год, то названные показатели имеют индекс 1.

Потребительский набор, содержащий 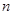товаров, обозначают вектором 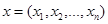, а цены товаров вектором цен 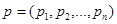. Далее все индексы записаны для случая двух товаров 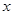и 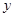с ценами 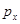и . И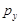ндексы в общем случае для 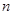товаров по существу не отличаются от индексов в частном случае.

Индекс номинального дохода 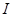определяется следующим образом:

.

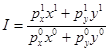Он показывает, во сколько раз вырос доход, если 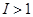, или снизился, если 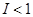, номинальный доход потребителя в текущем периоде по сравнению с базисным. На основе индекса номинального дохода нельзя сделать вывод об изменении реального благосостояния потребителя, которое зависит не только от величины номинального дохода, но и от объемов и структуры приобретаемых товаров, а также от изменения цен.

В индексе цен цены изменяются в текущем периоде, а потребительский набор остается неизменным. Если в индексе цен используется набор базисного периода, то это индекс Ласпейреса 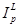. Если в индексе цен используется набор текущего периода, то имеем индекс Пааше 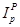. Индексы цен имеют вид:

, .

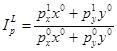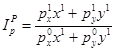Индекс цен Ласпейреса показывает, во сколько раз выросла стоимость потребительского набора базисного периода в текущих ценах относительно стоимости этого же набора в ценах базисного периода. Индекс цен Пааше показывает, во сколько раз выросла стоимость потребительского набора, купленного в текущем периоде, в текущих ценах по сравнению со стоимостью этого же набора в ценах базисного периода.

Индексы цен Ласпейреса и Пааше сами по себе не могут служить показателями динамики реального благосостояния потребителя, так как они не связаны с динамикой номинального дохода. Кроме того индексы цен не учитывают влияния изменения структуры потребительского набора, а потому точно не характеризуют изменение цен. Так, если 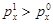, то 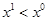, и наоборот, если 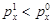, то 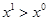. Поэтому индекс цен Ласпейреса, в котором в качестве весов используются объемы базисного периода, преувеличивает изменение цен в случае их роста и преуменьшает – в случае снижения. Индекс цен Пааше, в котором в качестве весов используются объемы товаров текущего периода, преуменьшает изменение цен в случае их роста и преувеличивает в случае их снижения.

В измерении изменения объемов приобретаемых товаров или изменения уровня жизни используются индексы, в которых объемы изменяются от одного периода к другому, а цены остаются неизменными. Если в качестве весов используются цены базисного периода, то имеем индекс Ласпейреса:

.

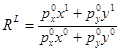Если в качестве весов используются цены текущего периода, по получим индекс Пааше:

.

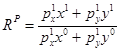Индексы объемов покупаемых потребителем товаров Ласпейреса и Пааше измеряют динамику реального дохода, в индексах используются неизменные цены.

Используем теорию выявленных предпочтений и индексы цен, номинального и реального дохода для оценки динамики благосостояния потребителя при переходе от базисного к текущему периоду.

Если 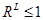, то 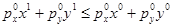. Это означает, что набор базисного периода выявлено предпочитается потребительскому набору текущего периода. Следовательно, благосостояние потребителя в базисном периоде было лучше, в текущем периоде оно снизилось. Если 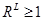, то 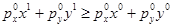. Неравенство означает, что в базисном периоде текущий набор потребителю был недоступен. В теории выявленных предпочтений сравниваются только доступные потребителю наборы. Недоступный набор может быть для потребителя более или менее предпочтительным, чем доступный набор. Поэтому неравенство 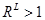не дает однозначного ответа на вопрос, снижается или растет благосостояние потребителя при переходе от базисного к текущему периоду.

Если 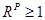, то 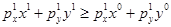. Это означает, что потребительский набор текущего периода выявлено предпочитается набору базисного периода. Если 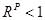, то 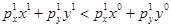. Здесь, как и в случае 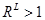, нет однозначного вывода о росте или снижении благосостояния потребителя при переходе от одного периода к другому.

Сравним индексы номинального дохода и индексы цен Ласпейреса и Пааше.

Если 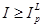, то 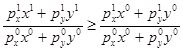. После сокращения обеих частей неравенства на положительное число в знаменателе дробей, получим выражение 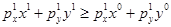. Эта ситуация имела место в случае 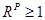и был сделан вывод о повышении благосостояния потребителя в текущем периоде по сравнению с базисным.

Если 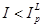, то 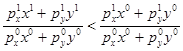. Этот случай аналогичен ситуации, когда 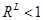и, следовательно, 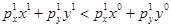. Здесь нет однозначного ответа о динамике благосостояния потребителя в текущем периоде по сравнению с базисным. Базисный набор или был недоступен потребителю в текущем периоде или изменились вкусы потребителя.

Случай 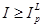сводится к случаю 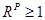, при переходе от базисного периода к текущему благосостояние потребителя выросло.

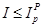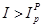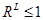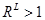Случаи и аналогичны случаям и . В случае 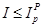благосостояние потребителя повысилось, в случае 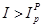не существует однозначного ответа об изменении благосостояния потребителя.

Сравнение индексов цен и дохода для населения всей страны, региона, социальных групп позволяет оценивать изменение их благосостояния за любые периоды времени.

5.3. Полезность фон Неймана-Моргенштерна

В анализе поведения потребителя фон Неймана-Моргенштерна совместно используется теория полезности и теория вероятности. Она основана на аксиомах о вероятностной совокупности наборов товаров. В результате обосновывается функция полезности, обладающая измерительными свойствами, которые можно использовать в процессе принятия решений в условиях риска. Такие функции называются функциями полезности фон Неймана-Моргенштерна.

Основным понятием рассматриваемой теории полезности является лотерея, которая определяется как множество наборов, каждый из которых может быть получен с заданной вероятностью. Так, набор 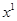может быть получен с вероятностью 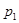, набор 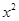- с вероятностью 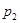, …, набор 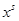- с вероятностью 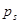. Лотерею представим в ви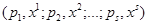де: , где 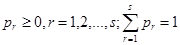. Если набор 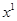выигрывает наверняка, то лотерея 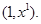Если лотерея 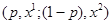, то набор 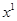выигрывает с вероятностью 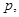а набор 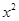с вероятностью .

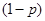Согласно первой аксиоме полезности фон Неймана-Моргенштерна предполагается существование отношения предпочтения, которое является совершенной полуупорядоченностью всех лотерей, является совершенным, транзитивным и рефлексивным. Безразличие ( ̴ ) и строгое предпочтение ( 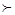) определены здесь так же, как и в теории потребительского поведения.

Аксиома монотонности состоит в следующем. Даны два набора 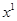и 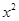, для которых 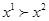; тогда 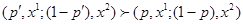, если и только если 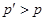. Это означает, что потребитель отдает предпочтение лотерее с большей вероятностью получить предпочитаемый набор. Набор, который получают наверняка, т.е. 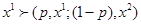для всех 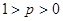, предпочтительнее любой лотереи, содержащей его и менее предпочтительный набор.

Аксиома непрерывности утверждает, что, если даны три набора 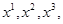для которых 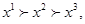тогда существует вероятность 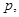для которой ̴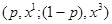 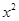, где 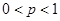. Т.е. выбранные лотереи интерполируют между предпочтениями в том смысле, что потребитель не делает различий между лотереей, содержащей более предпочтительный и менее предпочтительный наборы, и определенностью получения некоторого набора, занимающего промежуточное положение.

Аксиома о независимости не связанных между собой альтернатив отмечает: если заданы два набора 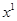и 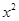, для которых ̴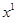 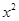, тогда для любого третьего набора 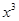справедливо ̴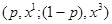 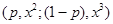, для всех 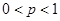. Присутствие третьего набора не нарушает предпочтений.

Аксиома о приведении сложных лотерей. Дано 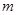лотерей: 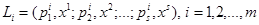. Рассмотрим сложную лотерею 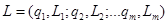, под которой имеется в виду лотерея, в которой в качестве исходов также выступают лотереи, а 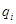- вероятность получить лотерею 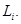Согласно аксиоме сложная лотерея может быть приведена к лотерее с подходящими вероятностями

̴

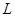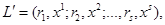
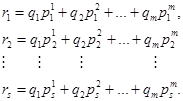
Основная теорема теории полезности фон Неймана-Моргенштерна утверждает, что при соблюдении названных аксиом существует функция полезности, определенная на всех лотереях, являющаяся однозначной с точностью до монотонного строгого возрастающего линейного преобразования. Так как одним из особых видов лотереи является набор, где 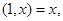то функция полезности определена для всех наборов. При этом 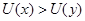, если и только если 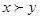. В общем виде 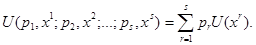Последнее означает, что полезность лотереи есть математическое ожидание полезности, равное взвешенной сумме полезностей наборов компонент, где в качестве весов выступают вероятности.

Функция полезности фон Неймана-Моргенштерна является однозначной с точностью до монотонного строгого возрастающего линейного преобразования в противоположность обыкновенным функциям полезности, которые являются однозначными с точностью до монотонного строгого возрастающего (линейного или нелинейного) преобразования. Таким образом, если 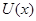- функция полезности, то 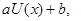где 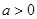, также является функцией полезности. Построим такую функцию полезности. Выберем числовые значения для двух уровней полезности; полезности других наборов оценивают соответствующим взвешиванием вероятностями. 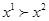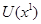Допустим и и 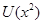- произвольные числа, для которых 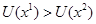. Они характеризуют уровни полезност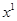и и 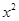соответственно. Например, 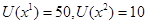. Чтобы определить полезность любого другого набора, взвесим эти значения полезностей вероятностями. Если 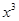- набор, для которого 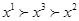, то по аксиоме непрерывности существует вероятность 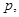для которой выполняется

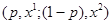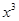̴ , (5.1)

поэтому .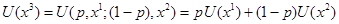

Первое равенство вытекает из того, что безразличные лотереи имеют одинаковые значения полезности. Второе равенство получено из определения полезности лотереи как математического ожидания ее полезности.

Допустим, 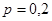обеспечивает выполнение условия (5.1). Тогда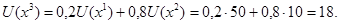

Аналогично, если для 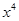выполняется условие 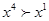, то по аксиоме непрерывности существует вероятность 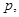для которой ̴ ,

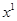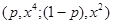Поэтому 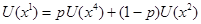, или 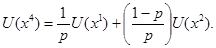Таким образом, после того как выбраны два произвольных числа, полезность шкалы фон Неймана-Моргенштерна определена.

Важным следствием теоремы о математическом ожидании полезности является правило рационального поведения в процессе принятия решения в условиях риска. Допустим предприниматель, принимающий решение, должен выбрать одну из 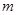стратегий: 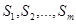, где исходом стратегии 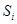является лотерея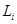

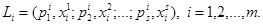
Величина 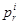характеризует вероятность выигрыша набора 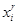при заданной стратегии 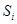. Полезность лотереи 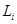оценивается как

.

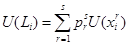Экономический субъект, принимающий решение, чтобы максимизировать полезность, выберет стратегию, которая обеспечивает наибольшее значение ожидаемой полезности

.

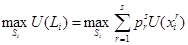Если имеется три возможные стратегии, для каждой из которых заданы вероятности выигрыша одной из двух альтернатив 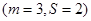, то оптимальной стратегии соответствует наибольший элемент главной диагонали следующей матрицы:

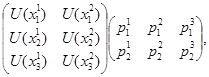
где в качестве матрицы полезностей выступает платежная матрица, а вторая матрица состоит из вероятностей.