ЕСЛИ(условие; действие1; действие 2)
Если условие истинное, то выполняется действие1, иначе - действие 2.
Пример. Пусть в ячейке Е2 хранится информация о баллах, набранных абитуриентом. Если колличество баллов меньше 10, то он принят в ВУЗ, иначе - нет. Формула будет выглядеть т.о.:
= ЕСЛИ (Е2>10; "принят"; "не принят").
Условная функция может быть вложенной. Пусть в том же ВУЗе существует правило: если абитуриент набрал 9 баллов, то он условно зачислен.
= ЕСЛИ(Е2>=10;"принят";ЕСЛИ(Е2=9;"принят условно";"не принят"))
Логика – наука о законах и формах мышления
Логика - наука, изучающая способы обоснования суждений, доказательства, мышления и логического вывода. В
математической логике используются для этого методы алгебры или теории алгоритмов.
Алгебра логики (булева алгебра) - раздел математики, изучающий методы оперирования логическими (булевыми)
переменными, принимающими только два значения - истина и ложь.
Алгебра логики - раздел математической логики, в котором изучаются логические операции над высказываниями.
Высказывания могут быть истинными, ложными или содержащими истину и ложь в разных соотношениях.
Математическая логика (теоретическая логика, символическая логика) - раздел математики, изучающий
доказательства и вопросы оснований математики.
Логическое высказывание - утверждение, которому всегда можно поставить в соответствие одно из двух логических
значений ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать
заглавными латинскими буквами. Высказывательной формой называется логическое высказывание, в котором один
из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма
превращается в высказывание.
Пример: A(x) = «В городе x идет дождь» A - высказывательная форма, x - объект.
Отрицание логического высказывания - логическое высказывание, принимающее значение «истинно», если исходное
высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний - логическое высказывание, истинное только тогда, когда они
одновременно истинны.
Дизъюнкция двух логических высказываний - логическое высказывание, истинное только тогда, когда хотя бы одно из
них истинно.
Импликация двух логических высказываний A и B - логическое высказывание, ложное только тогда, когда B ложно, а
A истинно.
Равносильность (эквивалентность) двух логических высказываний - логическое высказывание, истинное только тогда,
когда они одновременно истинны или ложны.
Кванторное логическое высказывание с квантором всеобщности ( ) - логическое высказывание, истинное
только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.
Кванторное логическое высказывание с квантором существования ( ) - логическое высказывание, истинное
только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.
Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно
Утверждение – суждение, которое требуется доказать или опровергнуть
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом
http://profbeckman.narod.ru/EVMУмозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается
(выводится) новое суждение
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят
переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может
принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0)
Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или
сложных) логических выражений, связанных с помощью логических операций.
Слово логика означает совокупность правил, которым подчиняется процесс мышления. Сам термин
«логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон».
Формальная логика - наука о формах и законах мышления. Законы логики отражают в сознании человека
свойства, связи и отношения объектов окружающего мира. Логика как наука позволяет строить формальные
модели окружающего мира, отвлекаясь от содержательной стороны. Основными формами мышления
являются понятия, суждения и умозаключения.
Понятие - форма мышления, которая выделяет существенные признаки предмета или класса предметов,
отличающие его от других. Например, компьютер, человек, ученики.
Суждения - это форма мышления, в которой утверждается или отрицается связь между предметом и его
признаком, отношения между предметами или факт существования предмета и которая может быть либо
истинной, либо ложной. Языковой формой выражения суждения является повествовательное предложение.
Вопросительные и побудительные предложения суждениями не являются. Суждения рассматриваются не с
точки зрения их смысла и содержания, а только с точки зрения их истинности или ложности. Истинным
будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных объектов.
«Дважды два равно четырём» - истинное суждение, а вот «Процессор предназначен для печати» - ложное.
Суждения могут быть простыми и сложными. «Весна наступила, и грачи прилетели» - сложное суждение,
состоящее из двух простых. Простые суждения (высказывания) выражают связь двух понятий. Сложные -
состоят из нескольких простых суждений.
Умозаключение - приём мышления, позволяющий на основе одного или нескольких суждений-посылок
получить новое суждение (знание или вывод). Примерами умозаключений являются доказательства теорем в
геометрии. Посылками умозаключения по правилам формальной логики могут быть только истинные
суждения. Тогда и умозаключение будет истинным. Иначе можно прийти к ложному умозаключению.
Исследования в алгебре логики тесно связаны с изучением высказывания (хотя высказывание –
предмет изучения формальной логики). С помощью высказывания мы устанавливаем свойства, взаимосвязи
между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно
ложно.
Математическая логика изучает вопросы применения математических методов для решения
логических задач и построения логических схем, которые лежат в основе работы любого компьютера.
Суждения в математической логике называют высказываниями или логическими выражениями. Подобно
тому, как для описания действий над переменными был разработан раздел математики алгебр а, так и для
обработки логических выражений в математической логике была создана алгебра высказываний, или алгебра
логики.
Таким образом, алгебра логики - раздел математической логики, в котором изучаются логические
операции над высказываниями. Высказывания могут быть истинными и ложными.
Логика высказываний послужила основным математическим инструментом при создании
компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним
битом (0 - ЛОЖЬ, 1 - ИСТИНА); тогда операция приобретает смысл вычитания из единицы; ∨ -
немодульного сложения; & (или ∧) - умножения; ↔ - равенства; ⊕ - в буквальном смысле сложения по
модулю 2 (исключающее Или - XOR); - непревосходства суммы над 1 (то есть AB = (A + B) <= 1).
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных
для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную
логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.
Таблицы истинности
Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).
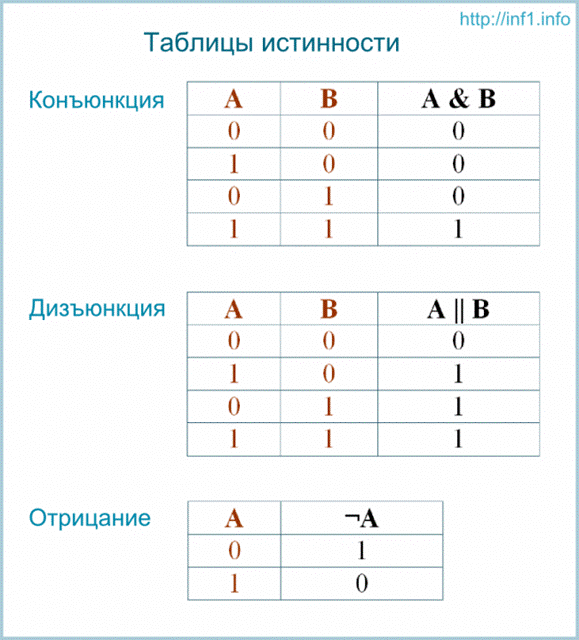
2 вопрос: В процессе обучения учащийся должен запомнить определенное количество важных сведений. Если он этого не сделает, то процесс познания или решения задачи замедлится, поэтому для облегчения процесса запоминания важно научить школьников пользоваться мнемоническими правилами.
Мнемоника - искусство запоминания - помогает нам выучить громоздкие формулы или правила, переводя их на язык смешных ассоциаций, созвучных фраз или стихов. Мнемонических правил много.
Цвета спектра по порядку (красный, оранжевый, желтый, зелёный, голубой, синий, фиолетовый):
1) Каждый Охотник Желает Знать, Где Сидит Фазан;
2) Как Однажды Жак-Звонарь Городской Сломал Фонарь;
3) Чому Олені Живуть Зимою Без Своїх Фантазій?
4) Чарівна Осінь - Життя Знову Б'є Сивий Фарфор
Запоминание порядка планет (от Солнца и к Солнцу): Плутон, Нептун, Уран, Сатурн, Юпитер, Марс, Земля, Венера, Меркурий
1) Планеты Нетрудно Упомнить Самому Юному Малышу, Зная Венеру, Меркурий;
2) Между Волками Зайчишка Метался, Юркнул, Споткнулся, Упал - Не Поднялся;
3) Можно Вылететь За Марс Ювелирно Свернув У Нашей Планеты;
4) Медвежонок Ветчину Закусил Малиной, Юркий Суслик Утащил Ножик Перочинный;
5) Маючи Великі Здібності Маленький Юрко Співав Українські Народні Пісні
Для запоминания спектральных классов звезд:
1) "Оh, Be a Fine Girl, Kiss Me";
2) Один Бритый Англичанин Финики Жевал Как Морковь.
Фазы Луны:
Чтобы отличить первую четверть от последней, наблюдатель, находящийся в северном полушарии, может использовать следующее мнемоническое правило. Если месяц похож на букву «С», то он Стареющий - это последняя четверть. Если он повёрнут в обратную сторону и тогда, мысленно приставив к нему палочку, можно получить букву «Р», то месяц «Растущий», то есть это первая четверть.
Физические формулы
1) Формула массы: Массу тела мы найдем, умножив плотность на объем;
2) Средняя скорость теплового движения частицы запоминается так: Три КоТа на Мясо;
3) Формула архимедовой силы: РоЖа - Во!
4) Закон электролиза: Масса КИТа
Приставки:
Жили ТРИ барана: Милли, Микро, Нано.
Здесь ключевое слово - три. Показатели степени этих приставок отличаются друг от друга как раз на три (10-3 ,10-6 ,10-9).
Для запоминания катодных и анодных процессов в электрохимии существует следующее мнемоническое правило:
- На аноде анионы окисляются.
- На катоде катионы восстанавливаются.
В первой строке все слова начинаются с гласной буквы, во второй — с согласной.
Римские цифры:
Для закрепления в памяти буквенных обозначений цифр в порядке убывания существует мнемоническое правило:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх.
Соответственно M(1000), D(500), C(100), L(50), X(10), V(5), I (1)
Введение в использование типов данных и свойств полей
 Показать все
Показать все
Эта статья содержит обзор типов данных и свойств полей и включает справочный раздел с подробными сведениями о типах данных. В этой статье также приведено краткое описание полей подстановок. Поля подстановок, одновременно допускающие несколько значений, в этой статье не обсуждаются. Ссылки на дополнительные сведения о полях подстановок, одновременно допускающих несколько значений, см. в разделе См. также.
В этой статье
· Общие сведения
· Справочные сведения о типах данных
Общие сведения
У каждого поля таблицы есть свойства. Эти свойства определяют характеристики полей и особенности работы с ними. Наиболее важным свойством поля является тип данных. Тип данных поля определяет, какого рода данные можно в нем хранить. Например, в поле с типом данных "Текстовый" можно хранить данные, содержащие текстовые и числовые символы, а в поле с типом данных "Числовой" можно хранить только числовые данные.
Тип данных поля определяет много других важных характеристик поля. Например:
· Использование поля в выражениях.
· Максимальный размер значения поля.
· Возможность индексирования поля.
· Допустимые форматы данных поля.
При создании нового поля в режиме конструктора указывается тип данных поля и (необязательно) его другие свойства.
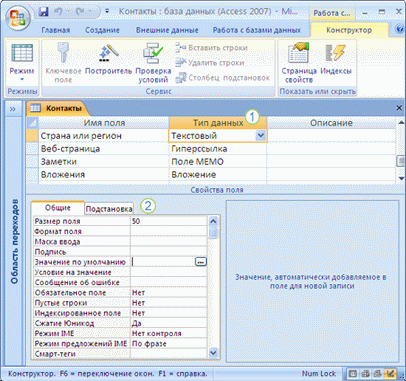
Таблица "Контакты" в режиме конструктора
 Тип данных
Тип данных
 Свойства поля
Свойства поля
При создании поля в режиме таблицы тип поля задается автоматически. Если поле создается в режиме таблицы с помощью шаблона поля или с использованием существующего поля из другой таблицы, тип данных уже определен в шаблоне или в другой таблице. Если поле создается методом ввода данных в режиме таблицы, тип данных назначается полю приложением Microsoft Office Access на основе вводимых значений. Если вводятся значения, тип данных которых отличается от типа данных поля, пользователю может быть предложено выбрать тип данных.
В режиме таблицы можно изменить тип данных поля и его свойства Формат поля, Индексированное поле и Обязательное поле.
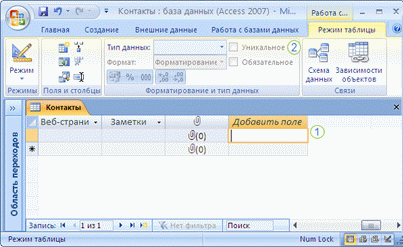
Таблица "Контакты" в режиме таблицы
 Создание поля посредством ввода данных в пустой столбец.
Создание поля посредством ввода данных в пустой столбец.
 Коррекция типа данных поля и других свойств с помощью вкладки Режим таблицы на ленте.
Коррекция типа данных поля и других свойств с помощью вкладки Режим таблицы на ленте.
Типы данных
Тип данных поля можно представлять себе как набор характеристик, которые относятся ко всем значениям, содержащимся в поле, и которые определяют, какого рода могут быть эти значения. Например, значения, которые хранятся в поле с типом данных "Текстовый", могут состоять только из букв, цифр и ограниченного набора знаков пунктуации. Кроме того, в таком поле может содержаться не более 255 символов.
В приложении Access предусмотрено 10 различных типов данных:
· Вложение. Файлы, например с цифровыми фотографиями. В одну запись можно вложить несколько типов данных. Этого типа данных не было в более ранних версиях Access.
· Счетчик. Числа, автоматически формируемые для каждой записи.
· Денежный. Значения денежных сумм.
· Дата/время. Значения даты и времени.
· Гиперссылка. Гиперссылки, например адреса электронной почты.
· Поле МЕМО. Крупные текстовые фрагменты, а также форматированный текст. Например, для подробного описания продукта обычно используется поле МЕМО.
· Числовой. Числовые значения, например расстояния. Обратите внимание, что для денежных значений предусмотрен отдельный тип данных.
· Поле объекта OLE. Объекты OLE, например документы Word.
· Текстовый. Короткие буквенно-цифровые значения, например фамилии или почтовые адреса.
· Логический. Логические значения.
СОВЕТ. Иногда кажется, что у данных в поле один тип данных, в то время как на самом деле у поля другой тип данных. Например, может показаться, что поле содержит численные значения, но на самом деле в нем записаны текстовые значения, например номера комнат. Для сравнения или преобразования значений с различными типами данных часто применяются выражения.
Поля подстановок
В качестве типа данных поля можно задать Мастер подстановок. При этом запускается мастер подстановок, с помощью которого создается поле подстановок. В поле подстановок отображается либо список значений, получаемый из таблицы или запроса, либо постоянный набор значений, задаваемый пользователем при создании поля.
В мастере подстановок можно либо ввести постоянный список значений, либо указать источник, из которого требуется получать значения, например поле в таблице. Типом данных поля подстановок может быть "Текстовый" или "Числовой", в зависимости от выбора пользователя в мастере подстановок.
ПРИМЕЧАНИЕ. Для полей подстановок предусмотрен дополнительный набор свойств поля, расположенный на вкладке Подстановка в области Свойства поля.
Дополнительные сведения о полях подстановок см. в разделе См. также.
Свойства поля
После того как создано поле и указан его тип данных, можно задать дополнительные свойства поля. Тип данных поля определяет, какие могут быть заданы другие свойства поля. Например, можно управлять размером текстового поля, задавая его свойство Размер поля.
Для числовых и денежных полей свойство Размер поля играет важную роль, поскольку оно определяет диапазон значений поля. Например, однобайтовые числовые поля могут содержать только целые числа в диапазоне от 0 до 255.
Свойство Размер поля определяет также размер места на диске, которое требуется для каждого значения числового поля. В зависимости от размера поля число может занимать в точности 1, 2, 4, 8, 12 или 16 байтов.
ПРИМЕЧАНИЕ. У текстовых полей и полей МЕМО размер значений поля может быть различным. Для этих типов данных свойство Размер поля задает максимальное место на диске, которое может быть использовано для одного значения.
Дополнительную информацию о свойствах полей и роли, которую они выполняют для различных типов данных, см. в разделе Справочные сведения о типах данных этой статьи.
