Критерии адекватности уравнений регрессии

Общепринятых критериев, характеризующих соответствие регрессии опытным данным и удовлетворяющих всем представлениям оптимальности, в настоящее время не существует.

Однако большинство исследователей вводят критерии, аналогичные дисперсии и выражающие среднеквадратическое отклонение в абсолютных или относительных величинах.

Например, в математической теории эксперимента используется остаточная дисперсия, величина которой характеризует рассеяние точек наблюдения относительно найденного уравнения регрессии.

В общем случае для исследователей представляет интерес величина отклонения наблюденных значений от кривой регрессии. Кроме того метрологов может интересовать величина приведенной погрешности наблюдения и получения кривой регрессии.

Таким образом, можно выделить следующие наиболее широко применяемые критерии [9, 12].

Для наблюденных значений:

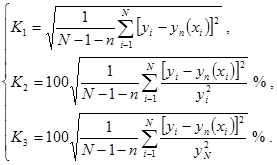
Для кривой регрессии:

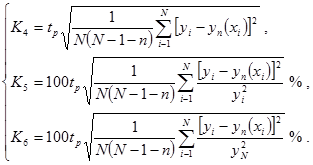
Величина 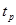- коэффициент Стьюдента для Р – процентного уровня вероятности. Для уровня вероятности Р = 95 % коэффициент Стьюдента может быть вычислен по эмпирической формуле

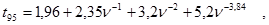
где 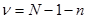- степень свободы.

Степень n полинома, описывающего кривую регрессии или количество параметров (n+1) , входящих в уравнение регрессии, как правило, выбирают произвольно, исходя из предыдущего опыта.

В большинстве случаев для практических расчетов принимают степень полинома равной двум или трем и в очень редких случаях равной пяти и более. Такое ограничение обычно связано с точностью вычислений, так как с увеличением степени погрешность вычислений нарастает катастрофически быстро. Другой существенной (самой главной) причиной является то, что необходимая точность может быть легко достигнута при использовании в качестве уравнения регрессии другой отличной от полинома функции.