НОРМАЛЬНЫЕ АЛГОРИТМЫ МАРКОВА. Цель работы: получить практические навыки в записи алгоритмов с использованием нормальных алгоритмов Маркова.

Цель работы: получить практические навыки в записи алгоритмов с использованием нормальных алгоритмов Маркова.

Теоретическая справка

Фиксируем некоторый алфавит 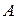. Пусть символы «стрелка» и «точка» не принадлежат алфавиту 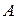: 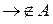, 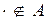. 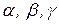– некоторые, возможно пустые, слова в алфавите .

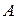Марковская подстановка (МП) – это операция над словами 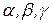, заключающаяся в следующем:

1) в исходном слове 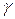ищется самое левое вхождение слова 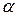, если оно существует, 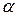заменяем на 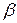в слове ;

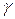2) полученное слово 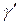является результатом применения марковской подстановки к слову ;

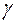3) если слово 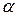не входит в слово 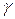, то говорят, что данная Марковская подстановка неприменима к слову .

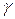Обычно МП записывается как .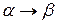

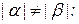в общем случае длины слов 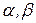могут не совпадать.

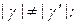длины слов 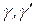в общем случае также могут не совпадать.

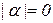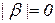Если или , то соответствующее слово является пустым. В МП пустое слово никак не обозначается и не занимает никакого места.

В любом слове 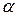имеется несколько вхождений пустого слова: перед первой буквой; после последней буквы; между любой парой букв внутри слова.

Частные случаи МП: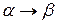

1. 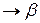, 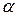– пусто: слово 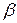приписывается перед .

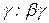2. 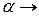, 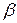– пусто: слово 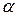исключается из .

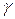Нормальным алгоритмом Маркова (НАМ) в алфавите 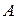называется упорядоченная конечная последовательность (столбец) Марковских подстановок типа: 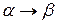или (и) 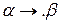, где 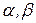– слова в алфавите 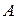, а символы 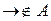и .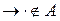

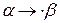– заключительная подстановка.

Запись НАМ – столбец подстановок вида .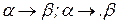

Функционирование НАМ

1. 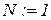, 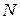– номер подстановки в схеме НАМ.

2. Выбирается 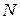-тая МП, пусть она имеет вид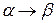

3. Левая часть подстановки 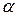ищется в преобразуемом слове .

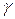4. Если 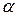найдено, то переход к пункту 7, иначе к пункту 5.

5.

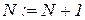
6. Если 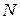не превышает общего числа подстановок, то переход к пункту 2, иначе – алгоритм заканчивает работу, останавливается.

7. Выполняется заме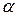на на 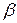в преобразуемом слове 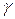(крайнее левое вхождение 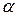в ).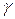

8. Если эта подстановка является заключительной, т.е. имеет вид 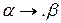, алгоритм останавливается, иначе переход к пункту 1.

После применения подстановки осуществляется заново просмотр столбца подстановок, а не продолжается просмотр .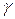

Процесс заканчивается, если:

- не найдена применяемая подстановка;

- выполнена заключительная подстановка.

Алфавит 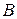называется расширением алфавита 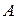, если .

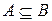Нормальный алгоритм над алфавитом 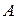– это нормальный алгоритм в алфавите 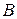, который слова в 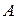, если он к ним применим, перерабатывает в слова в 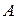. Нормальный алгоритм в 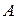может использовать только буквы алфавита .

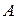Нормальный алгоритм над 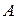может использовать вспомогательные символы. НАМ над 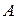более мощные, чем НАМ в А.

Одноместная частичная словарная функция 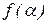, заданная в алфавите 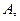называется нормально вычислимой, если существует НАМ над алфавитом 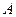, перерабатывающий слово 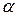в слово .

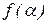Соответствие между нормальными алгоритмами и алгоритмами в интуитивном смысле выражает принцип нормализации – аналог тезисов Черча и Тьюринга: каков бы ни был алгоритм, для которого допустимыми исходными данными и результатом являются слова в некотором алфавите, существует эквивалентный ему НАМ в этом алфавите.

Пример 1. Нормальный алгоритм в алфавите 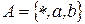, перерабатывающий каждое слово вида 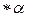в слово 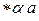, где слово 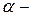слово, состоящее из букв .

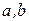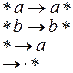
Пусть 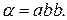Тогда, последовательность преобразований имеет вид:

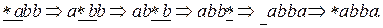
Пример 2. Нормальный алгоритм над алфавитом 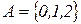стирающий все символы входного слова до первого символа 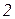включительно.

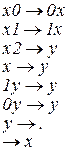
Здесь вспомогательные символы 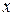и 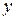, таким образом, алфавит 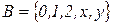. Буква 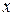служит для того, чтобы найти букву 2 последовательным перебором слева направо. Буква 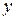позволяет стереть буквы 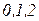движением справа налево.

Пример функционирования НАМ по переработке слова :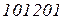

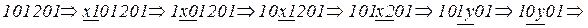
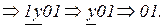
Пример 3. Нормальный алгоритм над алфавитом 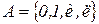, который выдает “и”, если в исходном слове, состоящем из нулей и единиц, есть комбинация 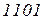, и “л”, в противном случае.

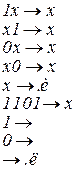
Приведем два примера функционирования НАМ:

1)

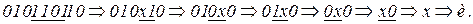
2)

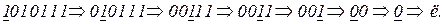
Пример 4. Пример НАМ, который работает бесконечно.

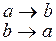
Задание на лабораторную работу

1. Составить нормальный алгоритм Маркова над алфавитом А.

2. На конкретных примерах исходных слов продемонстрировать работу составленных алгоритмов.

Варианты заданий

1. Реализовать алгоритм, выполняющий замену в слове 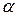в алфавите 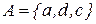каждого символа 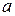на символ .

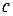2. Реализовать алгоритм, выполняющий перестановку в слове 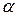в алфавите 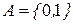букв таким образом, чтобы сначала стояли все нули, а затем все единицы.

3. Составить нормальный алгоритм, преобразующий исходную строку в алфавите 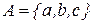в строку, в которой буквы расположены в алфавитном порядке.

4. Реализовать алгоритм, выполняющий 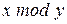над числами в унарном коде.

5. Реализовать алгоритм, выполняющий 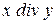над числами в унарном коде.

6. Реализовать алгоритм, выполняющий 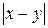над числами в унарном коде.

7. Реализовать алгоритм, вычисляющий арифметическое вычитание 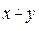в унарном коде.

8. Реализовать функцию выбор аргумента 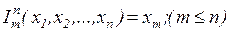над числами в унарном коде.

9. Реализовать вычисление предиката X=Y в унарном коде с сохранением (восстановлением) исходных данных.

10. Реализовать вычисление предиката X>Y в унарном коде с сохранением (восстановлением) исходных данных.

11. Реализовать алгоритм в алфавите 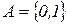, меняющий местами первую и последнюю буквы слова.

12. Реализовать алгоритм над алфавитом 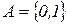, меняющий местами первый ноль и последнюю единицу.

13. Реализовать операцию копирование в алфавите 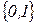, то есть получить из слова 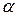слово .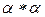

14. Реализовать алгоритм над алфавитом 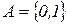, который выдает единицу, если в исходном слове только парные нули и ноль в противном случае.

15. Реализовать алгоритм в алфавите 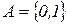, который переставляет буквы в слове 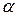так, чтобы сначала шли все нули, потом – единицы.

16. Реализовать алгоритм над алфавитом 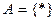, исключающий в слове последнюю звездочку.

17. Реализовать алгоритм, реализующий функцию циклический сдвиг двоичного числа на одну ячейку.

18. Реализовать алгоритм в алфавите 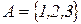, анализирующий последовательность цифр в слове и выдающий «+», если цифры образуют неубывающую последовательность, и «–» в противном случае.

19. Реализовать алгоритм над алфавитом 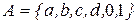, который выдает 1, если исходное слово содержит комбинацию baccd, и 0 - в противном случае.

20. Реализовать алгоритм, выполняющий следующие действия. В слове 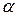в алфавите 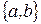стереть все, кроме 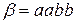. Если такой последовательности нет, все стереть.

21. Реализовать алгоритм над алфавитом 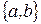, переставляющий буквы в обратном порядке.

22. Реализовать алгоритм над алфавитом 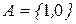, который выдает 1, если в исходном слове содержатся только парные нули, и 0 - в противном случае.

23. Реализовать алгоритм над алфавитом 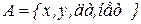, который выдает «да», если в исходном слове четное количество y-ков, и «нет» в противном случае.

24. Реализовать алгоритм над алфавитом 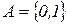, выдающий в результате столько единиц, сколько нулей в исходном слове.

25. Реализовать алгоритм над алфавитом 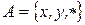, выделяющий часть слова расположенную между первой парой звездочек.

Контрольные вопросы

1. Что такое Марковская подстановка?

2. Что такое заключительная Марковская подстановка, как она обозначается?

3. В каком случае Марковская подстановка считается неприменимой к некоторому слову?

4. Как функционирует нормальный алгоритм Маркова?

5. В каких случаях НАМ заканчивает работу и останавливается?

6. Чем отличается НАМ в алфавите А от алгоритма над алфавитом А?

7. Привести пример бесконечно работающего нормального алгоритма Маркова.

8. Привести определение нормально вычислимой словарной функции.

9. Сформулировать принцип нормализации.