Составление алгоритма решения. Окончательный вариант математической формулировки и выбранный метод решения позволяют создать одношаговую схему алгоритма решения задачи 4.3
Окончательный вариант математической формулировки и выбранный метод решения позволяют создать одношаговую схему алгоритма решения задачи 4.3, представленную на рис. 4.9.
Созданная структура двойного последовательного ветвления при необходимом изменении содержимого вычислительных блоков может использоваться при решении любых задач, в которых требуется проверка двух взаимоисключающих условий, одно из которых – главное.
Алгоритм, как стандартный, содержит ряд параллельно расположенных блоков (7–12). Для возможности последующего программирования преобразуем его в две условно-линейные схемы (рис. 4.10).
В левой схеме естественный порядок выполнения блоков соответствует ветвям «НЕТ», а в правой – ветвям «ДА».
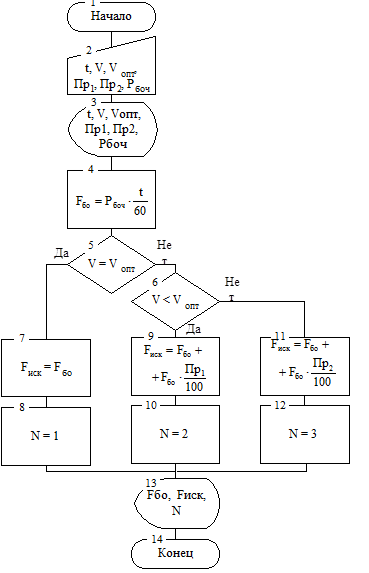
Рис. 4.9 Основная схема алгоритма задачи 4.3.
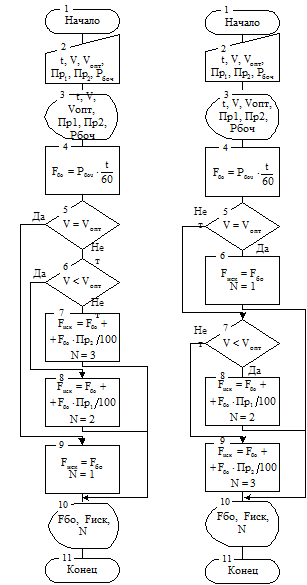
Рис. 4.10 Условно-линейные варианты схем алгоритма
Программирование задачи
Идентификация переменных представлена в табл. 4.8.
Таблица 4.8
| Обозначение в алгоритме | t | V | Vопт | Рбоч | Пр1 | Пр2 | Fбо | Fиск | N |
| Обозначение в программе | t | v | vopt | rb | pr1 | pr2 | fbo | f | n |
Условно-линейные схемы алгоритма и таблица идентификации позволяют составить программы решения задачи.
Программа по левой условно-линейной схеме
Особенность левой условно-линейной схемы – сохранение естественного порядка расчета при невыполнении отдельных условий и нарушение этого порядка, когда условия выполняются. Программирование такого варианта требует использования укороченного if.
/* Сложное ветвление. Укороченный if */
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
main( )
{
float t, v, vopt, rb, pr1, pr2, fbo, f;
int n;
scanf(“%f %f %f %f %f %f”, &t, &v, &vopt, &rb, &pr1, &pr2);
printf(“\n t=%.1f v=%.1f vopt=%.1f rb=%.1f”
“ pr1=%.1f pr2=%.1f ”, t, v, vopt, rb, pr1, pr2);
fbo=rb*t/60.; /* расход бензина при оптимальной скорости*/
if(vopt-0.01 <= v && v <= vopt+0.01) goto m1; /*переход */
/*к ветви 1*/
if(v<vopt) goto m2; /* переход к ветви 2 */
f = fbo + fbo * pr2/100.; /* ветвь 3 */
n=3;
goto m3;
m2: f = fbo + fbo * pr1/100.; /* ветвь 2 */
n=2;
goto m3;
m1: f = fbo; /* ветвь 1 */
n=1;
m3: printf(“\n fbo=%.2f f=%.2f n=%d ”, fbo, f, n);
}
5. 5. 5.
75.3 80. 91.2
80. 80. 80.
7.6 7.6 7.6
4.3 4.3 4.3
8. 8. 8.
Внимание! В программе впервые использован минимальный форматный ввод исходных данных – без указания общей длины каждого. Численные значения для обозначения окончания любого располагаются под программой, а затем вводятся столбцом (переход к следующей строке означает окончание ввода предыдущей). Три столбца численных значений вводимых переменных позволяют проверить все возможные вычислительные ветви (<, >, =).
Результаты счета представлены в приложении 4.5 (а, б, в).
Программа по правой условно-линейной схеме
Особенность правой условно-линейной схемы – сохранение естественного порядка расчета при выполнении отдельных условий и нарушение этого порядка, когда условия не выполняются. Программирование такого варианта требует использования полного if.
/* Сложное ветвление. Полный if */
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
main( )
{
float t, v, vopt, rb, pr1, pr2, fbo, f;
int n;
scanf(“%f %f %f %f %f %f”, &t, &v, &vopt, &rb, &pr1, &pr2);
printf(“\n t=%.1f v=%.1f vopt=%.1f rb=%.1f”
“ pr1=%.1f pr2=%.1f ”, t, v, vopt, rb, pr1, pr2);
fbo=rb*t/60.; /* расход бензина при оптимальной скорости*/
if(vopt - 0.01 <= v && v <= vopt + 0.01)
{
f = fbo; /* ветвь 1 */
n=1;
}
else
{
if(v<vopt)
{
f = fbo + fbo * pr1/100.; /* ветвь 2 */
n=2;
}
else
{
f = fbo + fbo * pr2/100.; /* ветвь 3 */
n=3;
}
}
printf(“\n fbo=%.2f f=%.2f n=%d ”, fbo, f, n);
}
5. 5. 5.
75.3 80. 91.2
80. 80. 80.
7.6 7.6 7.6
4.3 4.3 4.3
8. 8. 8.
Три столбца значений вводимых переменных позволяют проверить все возможные вычислительные ветви (<, >, =).
Результаты счета представлены в приложении 4.6 (а, б, в).
Анализ полученных программ позволяет сделать вывод о предпочтительности варианта с полным if (отсутствуют метки операторов). Следовательно, при составлении условно-линейной схемы алгоритма сложного ветвления рекомендуется вариант «ДА, ДА, …, ДА» естественного порядка решения.
