Упражнения. 4.3.1. Задан абстрактный алфавит в виде упорядоченного дискретного множества символов

4.3.1. Задан абстрактный алфавит в виде упорядоченного дискретного множества символов. Дайте название алфавиту и определите его мощность.

а) A, Б, B, …, Я, [алфавит букв русского языка, мощность, которого n =33];

б) 0, 1, 2, …, 9, [алфавит арабских цифр, n =10;

в) × , : , 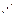, , 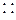, 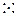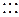[алфавит знаков шестигранной кости (кубика), n=6];

г) B= {0, 1}, [двоичный алфавит, n_B=2];

д) {×;—;L}, [двоичный алфавит знаков азбуки Морзе {«точка», «тире», «пробел»}, n=3];

е) I, V, X, L, C, D, M…; [алфавит римской системы счисления];

ж)

[алфавит языка блок-схем для изображения алгоритмов, n=6].

з) {и;л}, [двоичный алфавит языка алгебры логики «истина», «ложь», n=2];

и) {+,–, 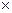, :} [алфавит знаков арифметических операций, n=4];

к) { 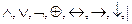} [алфавит знаков операций языка алгебры логики, n=8];

л) придумайте свой абстрактный алфавит в виде упорядоченного дискретного множества символов.

4.3.2.Задано алфавитное кодирование 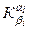и кодирующий алфавит {0, 1, 2}. Можно ли пользоваться таким кодом, будет ли он однозначно кодировать?

а) С = {001, 0210, 1001, 2001, 001221, 0101210};

б) С = {201, 01202, 202, 02001, 201010, 1201121, 111201};

в) С = {012, 0112, 1200, 2012100, 101210, 012120};

г) С = {010, 102, 10121, 0102, 101012};

д) С = {011, 012, 0112, 1011, 0101, 10112, 01112};

е) С = {000, 00100, 1000, 0001001, 0010010}.

ж) С = {01, 102, 012, 0102, 02012};

з) С = {01, 101, 210, 121, 02101, 01121};

и) С = {101, 1001, 2101, 201, 0210, 101102, 210101};

к) С = {01, 10, 210, 201, 0210, 011022, 101221};

л) придумайте свой кодирующий алфавит в виде упорядоченного дискретного множества символов и задайте алфавитное кодирование 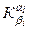так, чтобы им можно было пользоваться (код однозначно кодировал).

Образец: С = {11, 112, 011, 01210, 20120, 11220};

Решение: заданное алфавитное кодирование С не может однозначно кодировать, т.к. код не является префиксным. В частности, первое слово «11» одновременно является началом как второго слова «112», так и последнего – «11220».

4.3.3. Задача –модель. Алфавитное кодирование 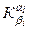задано схемой σ:

σ= .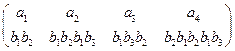

Допускает ли код однозначное декодирование?

Решение: Пользуясь общим критерием взаимной однозначности, установим, обладает ли заданное кодирование свойством однозначности.

1) Выпишем все нетривиальные разложения каждого элементарного кода:

,

,

,

.

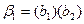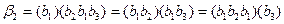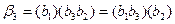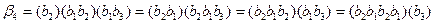2) Составим множество M₁, включая в него слова, входящие в качестве начал в нетривиальные разложения элементарных кодов:

.

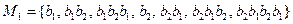3) Составим множество M₂, включая в него слова, которые являются окончаниями нетривиальных разложений элементарных кодов:

.

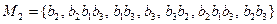4) Составим множество M=M₁ÇM₂ÈL={L; b₂; b₁b₃}.

5) Выпишем все разложения элементарных кодов, связанных с элементами множества M так, чтобы в каждом из них присутствовал в качестве начала или конца любой из трех его элементов. В тех разложениях, где в качестве начала или конца нет непустых элементов из этого множества М (т.е. b₂ или b₁b₃), мы «дописываем» недостающие начало или конец с помощью третьего элемента из множества М – с помощью символа L. Имеем:

,

,

.

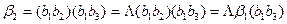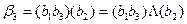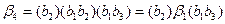Поясним построение разложений:

– т.к. разложение b₂ содержало только один из двух непустых элементов множества М, то в качестве второго элемента добавим символ L, но т.к. b₂ содержит элемент b₁b₃ в качестве окончания, то символ L добавляем в качестве начала;

– разложение b₃ содержало два непустых элемента из множества М – b₂ и b₁b₃, поэтому мы их сохраним в качестве начала и конца, а символ L включим для того, чтобы им назвать соответствующую дугу ориентированного графа;

– разложение b₄ содержало два непустых элемента из множества М – b₂ и b₁b₃, которые сохраним в качестве начала и конца, а также элемент b₁b₂, который представляет собой разложение b_1.

6) По полученным разложениям построим ориентированный граф, вершины которого – элементы множества 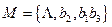. Пару вершин соединяем дугами тогда и только тогда, когда существует разложение, в которое элементы множества М (вершины графа) входят в качестве начала и конца, учитывая их порядок в этом разложении (рис.2).

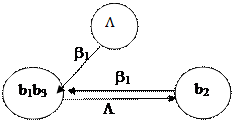Рис.2

7) В графе G (рис. 2) отсутствуют контуры и циклы, проходящие через вершину Λ. Поэтому, согласно теореме Маркова, алфавитное кодирование с заданной схемой являются взаимно-однозначным. Т.о., заданный код можно однозначно декодировать.

Например, декодируем этим кодом слово 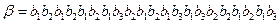. Имеем: 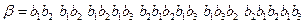. Тогда исходное слово имело вид: .

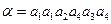4.3.4.Алфавитное кодирование 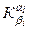заданокодирующими алфавитами A и В, а также таблицей кодов s (схема). Можно ли пользоваться таким кодом, будет ли он однозначно кодировать?

а) A={0,1,2,3,4.5,6,7,8,9}, В={0,1} и

.

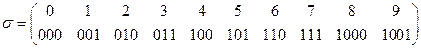б) A={0,1,2,3,4.5,6,7,8,9}, В={0,1} и

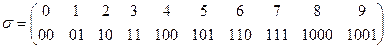
в) A={0,1,2,3,4.5,6,7,8,9,A,B,C,D,E,F}, В={0,1} и

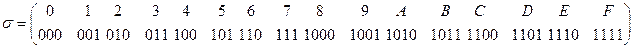г) A={0,1,2,3,4.5,6,7,8,9,A,B,C,D,E,F}, В={0,1} и

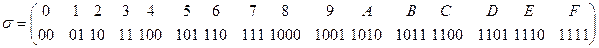
д) A={a₁, a₂, a₃, a₄, a₅ }, В={b₁, b ₂, b ₃, b ₄, b ₅} и

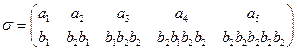
е) A={a₁, a₂, a₃, a₄, a₅ }, В={b₁, b ₂, b ₃, b ₄, b ₅} и

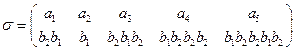
ж) A={a₁, a₂, a₃, a₄, a₅ }, В={b₁, b ₂, b ₃, b ₄, b ₅} и

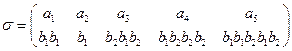
з) A={a₁, a₂, a₃, a₄, a₅ }, В={b₁, b ₂, b ₃, b ₄, b ₅} и

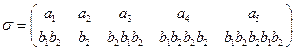
и) A={a₁, a₂, a₃, a₄, a₅ }, В={b₁, b ₂, b ₃, b ₄, b ₅} и

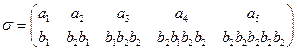
к) A={a₁, a₂, a₃, a₄, a₅ }, В={b₁, b ₂, b ₃, b ₄, b ₅} и

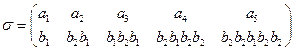
л) придумайте свой кодирующий алфавит в виде упорядоченного дискретного множества символов и задайте алфавитное кодирование 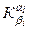таблицей кодов (схемой). Можно ли пользоваться таким кодом, будет ли он однозначно кодировать?

Образец 1. Заданы алфавиты А={0,1,2,3,4.5,6,7,8,9} и В={0,1} и таблица кодов (схема) 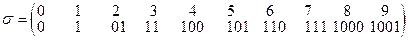. Допускает ли код однозначное декодирование? [Нет, например, 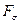(333)=111111= 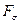(77), т.е. такое кодирование не допускает однозначного декодирования]

Образец 2. Заданы алфавиты А={0,1,2,3,4.5,6,7,8,9} и В={0,1} и таблица кодов (схема) 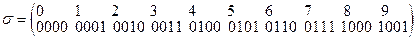. Допускает ли код однозначное декодирование? [Да. Такое кодирование допускает однозначное декодирование]

Образец 3.Установите, является ли кодирование 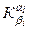={a, ba, cab, babc} взаимно– однозначным.

Решение: Согласно алгоритму, имеем:

1) Выпишем все нетривиальные разложения каждого элементарного кода:

b₁=(a)

b₂=(b)(a)

b₃=(c)(ab)=(c a) (b)= (c)( a)(b)

b₄=(ba)(b)(c)=(ba)(bc) =(b)(ab)(c) =(bab)(c) =(b)(abc)

2) Составим множество M₁, включая в него слова, входящие в качестве начал в нетривиальные разложения элементарных кодов:

M₁={b, c, ca, ba, bab}.

3) Составим множество M₂, включая в него слова, которые являются окончаниями нетривиальных разложений элементарных кодов:

M₂={a, b, ab, c, bc, abc}.

4) Составим множество M=M₁ÇM₂ÈL={b, c, L}

5) Выпишем все разложения элементарных кодов, связанных с элементами множества M так, чтобы в каждом из них присутствовал в качестве начала или конца любой из трех его элементов. В тех разложениях, где в качестве начала или конца нет непустых элементов из этого множества М (т.е. b или c), мы «дописываем» недостающие начало или конец с помощью третьего элемента из множества М – с помощью символа L. Для разложения b₄ не нашлось разложений, соответствующих перечисленным требованиям, Поэтому ему символы L были добавлены и в качестве начала, и в качестве конца. Имеем:

b₂=(b) b₁L

b₃=(c)b₁ (b)

b₄=Lb₄L

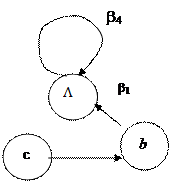
6) Строим граф G_s (Рис. ). Петля у вершины L означает, что соответствующее этому графу кодирование не является взаимно-однозначным.

4.3.5. Задача–модель.Постройте код Шеннона-Фано для русского алфавита.

Решение: Один из эффективных путей кодирования основан на применении основной теоремы К.Шеннона для каналов без шума.

Для построения кода методом Шеннона-Фано буквам алфавита ставят соответствие их частоты (статистическую вероятность) в порядке убывания вероятности.

Алгоритм:

1) Составим таблицу кодов, учитывая вес каждой буквы алфавита (т.е. ее статистическую вероятность), с помощью дихотомического деления. Разделим множество букв алфавита на два подмножества, уравнивая суммарные вероятности каждой группы.

2) Суммируя вероятности появления букв выясняем, что приблизительно равные суммы получаются для пробела ( знак L) и множества букв {о,е,ё,а,и,т} – с одной стороны и всех остальных букв – с другой стороны. Первому подмножеству присваиваем символ «0», второму – «1».

3) Продолжим деление букв на два приблизительно равных по вероятности подмножества: буквам алфавита {L,о} присваиваем символ «0», остальным буквам этого подмножества – {е,ё,а,и,т}символ – «1». Аналогично, в следующем подмножестве символ «0» присваиваем буквам алфавита {н,с,р,в,л,к}, а символ «1» – всем буквам от «м» до «ф».

4) Процесс разделения на подмножества продолжим до тех пор, пока в каждой подгруппе не окажется по одной букве. Результаты занесем в таблицу (Табл. )

	Двоичные знаки
Буква	1-й	2-й	3-й	4-й	5-й	6-й	7-й	8-й	9-й	Код
L
о
е
а
и
т
н
с
р
в
л
к
м
д
п
у
я
ы
з
ъ, ь
б
г
ч
й
х
ж
ю
ш
ц
щ
э
ф

5) Т.о., каждая буква русского алфавита получила свой двоичный код, результаты которого представим в таблице (Табл.) Такой код является префиксным, однако код Шеннона-Фано не всегда приводит к однозначному построению кода, т.к. разбиение на группы произвольно. Эту процедуру можно представить в виде двоичного дерева (Рис.).

4.3.6.Декодируйте слово, закодированное кодом Шеннона-Фано (задача 4.3.5). Определите, является ли этот код префиксным, разделимым, взаимно однозначным.

а) 11000 0101 0111 0100 11000 0101 0111 0110 10111 0101 [ математика]

б) 1011 10100 110100 111011 [круг]

в) 10110 001 111011 0110 10111 0101 [логика]

г) 111111110 0110 10110 0100 10100 [Эйлер]

д) 111011 0101 110100 1001 1001 [Гаусс]

е) 10110 0100 0110 111010 0110 11111101 [Лейбниц]

ж) 1000 111001 1111101 0111 001 1000 [Ньютон]

з) 10110 001 111010 0101 111100 0100 10101 1001 10111 0110 0110 [Лобачевский]

и) 0100 10101 10111 10110 0110 110010 [Евклид]

к) 110011 0110 111111111 0101 111011 001 10100 [Пифагор]

4.3.7. Задача-модель: Пусть заданы алфавиты А={х, у}, В={0,1}и разделяемая схема 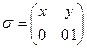. Тогда 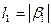=1 (для слова «0»), 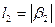=2 (для слова «01». При распределении вероятностей (0.5, 0.5) цена кодирования равна

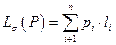=0,5 ∙ 1 + 0,5 ∙ 2 = 1,5,

а при распределении вероятностей (0.8, 0.2) соответственно

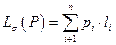=0,8 ∙ 1 + 0,2 ∙ 2 = 1,2 .

4.3.8. Для списка сообщений с заданным распределением частот постройте код Фано. Вычислите стоимость кода.

а)	S	T	U	V	W	X	Y	Z
	0,18	0,11	0,14	0,05	0,3	0,14	0,02	0,06
б)	S	T	U	V	W	X	Y	Z
	0,02	0,23	0,16	0,05	0,2	0,14	0,12	0,08
в)	S	T	U	V	W	X	Y	Z
	0,18	0,21	0,11	0,1	0,2	0,12	0,05	0,03
г)	S	T	U	V	W	X	Y	Z
	0,17	0,22	0,14	0,1	0,2	0,11	0,04	0,02
д)	S	T	U	V	W	X	Y	Z
	0,08	0,01	0,11	0,1	0,2	0,22	0,15	0,13
е)	S	T	U	V	W	X	Y	Z
	0,17	0,24	0,15	0,12	0,15	0,11	0,04	0,02
ж)	S	T	U	V	W	X	Y	Z
	0,09	0,01	0,21	0,11	0,12	0,22	0,11	0,13
з)	S	T	U	V	W	X	Y	Z
	0,07	0,14	0,15	0,12	0,25	0,11	0,17	0,09
и)	S	T	U	V	W	X	Y	Z
	0,19	0,11	0,21	0,11	0,12	0,12	0,11	0,03
к)	S	T	U	V	W	X	Y	Z
	0,08	0,1	0,15	0,15	0,3	0,05	0,12	0,05

[а) 2,72; к) 1 вариант – 2,83; 2 вариант – 2,83]

л) Придумайте и решите аналогичную задачу: задайте список сообщений с заданным распределением частот и постройте код Фано. Вычислите стоимость кода.

Образец:

S	T	U	V	W	X	Y	Z
0,12	0,23	0,16	0,1	0,2	0,14	0,02	0,03

Решение:

1) Запишем сообщения в порядке убывания частот (при равенстве частот порядок сообщений выбирается произвольно). Имеем:

T	W	U	X	S	V	Z	Y
0,23	0,2	0,16	0,14	0,12	0,1	0,03	0,02

2) Разделим множество символов на два численно малоразличимых подмножества: два первых символа дают сумму 0,43, все остальные – 0,57. Первому подмножеству поставим в соответствие символ «0», второму – «1». На следующем этапе присвоения двоичных знаков первое подмножество букв легко делится на две части: букве «T» присваивается второй знак «0», букве «W» – «1». Во втором подмножестве дихотомическое деление произведем с учетом суммирования относительных частот: для букв «U» и «X» сумма частот равна 0,16+0,14=0,30, тогда, как для букв «S», «V», «Z» и «Y» сумма частот равна 0,27 . Поэтому буквам «U» и «X» присваиваем второй двоичный знак «0», а буквам «S», «V», «Z» и «Y» – «1». Продолжая этот процесс до конца, его результаты занесем в таблицу (Табл)

Буквы алфавита	Двоичные знаки
1-й	2-й	3-й	4-й	5-й	Коды
T	0,23
W	0,2
U	0,16
X	0,14
S	0,12
V	0,1
Z	0,03
Y

3) Вычислим стоимость кода. Для этого надо учесть и частоту букв, и количество символов его двоичной записи. Подсчитаем стоимость кода, с учетом соответствующих вероятностей и того, что буквы T и W имеют длину l=2, буквы U, X и S имеют длину l= 3, буква V имеют длину l= 4, а буквы Z и Y имеют длину l=5:

L_b(p) = 2× (0,23+0,2)+3× (0,16+0,14+0,12)+4×0,1+5× (0,03+0,02)=2,77.

4.3.9.Постройте схему s и кодовое дерево для заданных кодов. Определите, является ли этот код блочным и префиксным.

а) a₁=000, а₂=010, а₃=01, а₄=1010, а₅=10, а₆=1110, а₇=1111

б) a₁=0000, а₂=1011, а₃=1010, а₄=100, а₅=0110, а₆=1000, а₇=110

в) a₁=111, а₂=1001, а₃=010, а₄=1101, а₅=1010, а₆=101, q=10

г) a₁=1000, а₂=011, а₃=0110, а₄=0000, а₅=0100, а₆=111, а₇=001.

д) a₁=10, а₂=0101, а₃=110, а₄=0010, а₅=100, а₆=11, а₇=101.

е) a₁=110, а₂=01, а₃=1101, а₄=0110, а₅=1010, а₆=1110, а₇=11.

ж) a₁=1000, а₂=0001, а₃=01, а₄=1110, а₅=10010, а₆=11010, а₇=1011.

з) a₁=101, а₂=001, а₃=011, а₄=0110, а₅=1001, а₆=1110, а₇=10101.

и) a₁=10011, а₂=1001, а₃=1011, а₄=10110, а₅=01001, а₆=10, а₇=101.

к) a₁=1001, а₂=01, а₃=0101, а₄=10110, а₅=10001, а₆=110, а₇=101.

л) Придумайте и решите аналогичную задачу.

Образец:

a₁=100, а₂=0111, а₃=010, а₄=0000, а₅=0101, а₆=1011, а₇=01.

Решение: Схема кода имеет вид:

.

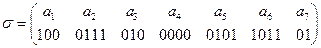Построим кодовое дерево для заданного кода. Корнем двоичного кодового дерева является пустой символ «L».Ветви двоичного дерева соединяют те и только те вершины, которые служат соседними символами в двоичной записи соответствующего кодового слова. Вершины получают метки, состоящие из символов «0» или «1», в зависимости от производимого дихотомического деления.

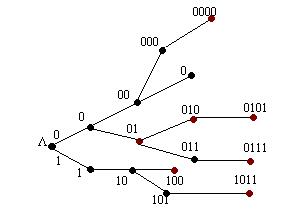
Заданный код не является префиксным, т.к. есть слова, являющиеся началом других слов. Так, началом слова l=0101 служит слово l=010. В свою очередь, началом слова l=010 служит слово q=01.

4.3.10. Задача-модель.Алфавит из восьми символов представлен в кодовой таблице 6.4. без учета статистических характеристик (табл.6.4а) и с учетом вероятности (табл. 6.4б). Постройте кодовое дерево для заданных кодов.

Буквы	вероятности	Кодовые Комбинации без учета статистических характеристик		Кодовые комбинации с учетом статистических характеристик
Z1	0,22
Z2	0,20
Z3	0,16
Z4	0,16
Z5	0,10
Z6	0,10
Z7	0,04
Z8	0,02

Табл.6.4 а) б)

Решение: На рис.136 показан алфавит кодирования, состоящий из восьми символов.

Рис.136 (Проверить!)

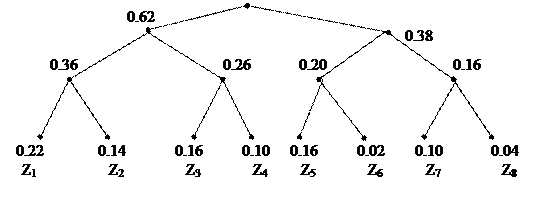В этом примере энтропия набора букв Н≈2,84, что ведет к неоднозначному кодированию и затрудняет работу по этому коду.

В решении этой задачи отсутствие помех служит ограничением при реальном кодировании. Если учесть вероятность 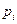появления сообщения 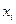содержащего 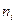символов алфавита В, то среднее значение количества символов из В можно найти по формуле 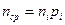, где n_ср=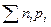

Среднему числу символов соответствует максимальная энтропия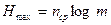

4.3.11. Составьте коды:

а) e(20)	б) e5(20)	в) e (25)	г) e5(25)	д) e (30)
е) e6(30)	ж) e7(30)	з) e (35)	и) e7(35)	к) e8(35)

Образец: Составьте коды: e(45), e₇(45) e₈(45).

Решение: Т.к. 45₁₀=101101₂, то e(45) =101101, e₇(45) =0101101, e₉(45) =000101101.

…