I.I4. Показатели точности и формы представления результатов измерений

В соответствии с [6] устанавливаются следующие показатели
точности измерений:

интервал, в котором погрешность измерения находится с заданной вероятностью; .

интервал, в котором систематическая погрешность измерения находится с заданной вероятностью;

числовые характеристики систематической составляющей погреш­ности измерения;

числовые характеристики случайной составляющей погрешности измерения;

функция распределения или плотность вероятности систематической составляющей погрешности измерения;

функция распределения или плотность вероятности случайной составляющей погрешности измерения.

В соответствии с принятыми показателями точности ГОСТ 8,011-72 [6] устанавливает следующие формы представления результатов измерений:

1. Если точность измерений выражена интервалом, в котором с установленной вероятностью находится суммарная погрешность измере­ния, то результат измерений представляют в форме

Q; D от D_н до D_в; P,

где Q –результат измерения в единицах измеряемой величины;

D, D_н ,D_в - соответственно погрешность измерения с нижней и верхней её границами, в тех же единицах: р - установленная веро­ятность, с которой погрешность измерения находится в этих грани­цах.

Пример: 121м/с ; D от – 1 до 2м/с; р = о, 99.

2. Если точность измерений выражена интервалом, в котором с установленной вероятностью находится систематическая составляющая погрешности измерения, а для случайной составляющей погрешности измерения – стандартной аппроксимацией функции распределения и сред­ним квадратическим отклонением случайной составляющей погрешности, устанавливается следующая форма представления результатов измерения:

Q ; D_с от D_сн до D_св; р_с ;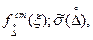

где D_с ;Dсн ; Dсв – соответственно систематическая составляющая
погрешности измерения, нижняя и верхняя её границы; р_с - заданная
вероятность, с которой систематическая составляющая погрешности
находится в этих границах; .

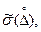- оценка среднего квадратического отклонения случайной сос­тавляющей погрешности измерения в единицах измеряемой величины;

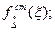- стандартная аппроксимация функции распределения случайной составляющей погрешности измерения. Стандартом рекомендуются сле­дующие функции распределения: нормальная, треугольная, трапециевид­ная, равномерная, антимодальные I и II, Релея.

Пример: 12,74 Гн; D_с от 0,11 до 0,17 Гн; Рс= 0,99; 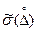= 0,10 Гн; равн.

3. Если точность измерений выражена стандартными аппроксима­циями функций распределения систематической и случайной составляю­щих погрешности измерения и их средними квадратическими отклонени­ями, то устанавливается следующая форма представления результатов измерения:

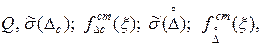
где 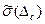- оценка среднего квадратического отклонения систематической составляющей погрешности измеряемой величины; 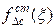- стандартная аппроксимация функции распределения систематической величины погрешности.

Пример: 12,60 В; 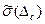= 0,02 В; равн.; 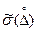= 0.01В; норм.

4. Если точность измерений выражена функциями распределения систематической и случайной составляющих погрешности измерения, устанавливает следующую форму представления результатов измерения:

Q;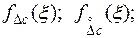

где 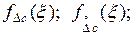соответственно функции распределения (плот­ности вероятностей) систематической и случайной составляющих пог­решности измерения, которые могут быть заданы таблицами, графика­ми или формулами, причем обе функции должны задаваться в одинако­вой форме.

При технических измерениях, которые выполняются однократно, погрешность измерений определяется погрешностью средств измерений. Эта погрешность известна до измерения из нормативно-технической документации. В указанном случае погрешность записывают в виде предела допускаемой суммарной погрешности, а вероятность не указывают, предполагая её значение р =0,997.

Значащих цифр численных показателей точности измерений долж­но быть не более двух, но в промежуточных выкладках необходимо удерживать по три-четыре значащие цифры, чтобы уменьшить погреш­ности округления.

Числовое значение результата измерения должно быть представ­лено с учетом погрешности, с которой это измерение выполнено. Младший разряд результата должен соответствовать разряду погреш­ности.