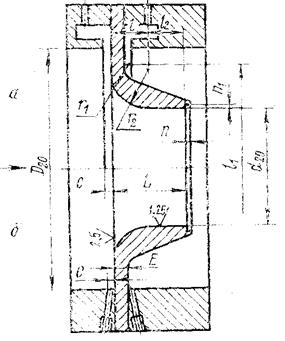
Чертеж сужающего устройства

РАСЧЕТ РАСХОДОМЕРА

1.1 Определяю недостающие данные для расчета:

1) Абсолютное давление измеряемой среды перед сужающим устройством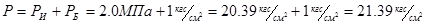

2) Диаметр трубопровода при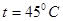

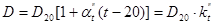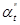, где - средний коэффициент линейного теплового расширения материала сужающего устройства.

в диапазоне температур от – 20 до + 60⁰С можно принять 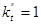, значит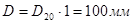

3) Динамическая ( 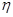) и кинематическая ( 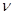) вязкости газа берутся из таблицы приложения 1 этого документа.

,

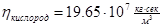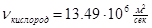
4) Показатель адиабаты ( 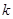) определяется из приложения 2.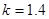

5) Коэффициент сжимаемости ( 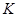), характеризующий отклонение данного газа от законов идеального газа определяю из рис 1.

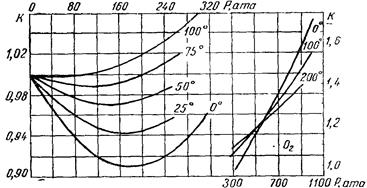
Рис. 1. Коэффициент сжимаемости кислорода

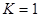
6) Плотность газа в рабочем состоянии ( ).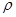

Нормальным состоянием газа для промышленных измерений считается такое состояние, при котором температура газа 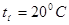( 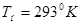), давление 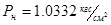, а влажность .

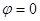Значение плотности газа в нормальном приведено в таблице приложения 3.

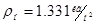
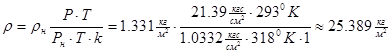
Выбрал сопло и манометр

1) Для сопла по заданному значению 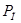и условию 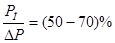из Рис. 2. определяю предельный номинальный перепад давления дифманометра 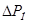и модуль сужающего устройства .

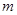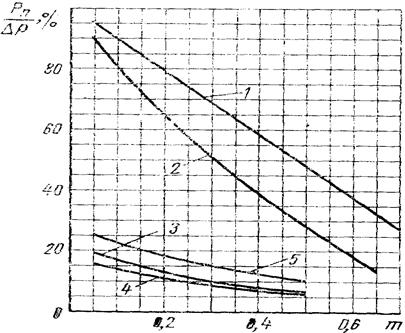
Рис. 2. Потеря давления в сужающем устройстве:

1-диафрагма; 2-сопло; 3-короткое сопло Вентури;

4-длинное сопло Вентури

,

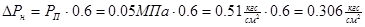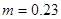
2) По значению 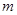вычисляю коэффициент расхода 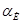, т.к.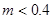

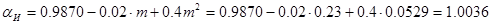
и определяю значение коэффициента расхода 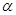(с учетом поправочного множителя на шероховатость трубопровода ).

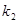Поправочный множитель 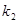для 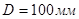определяется из Рис. 3.

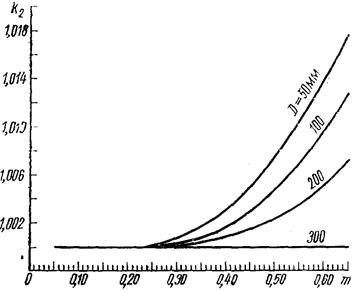
Рис. 3. Поправочный множитель на шероховатость трубопровода для сопел и сопел Вентури

,

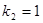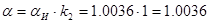
3) Определяю число Рейнольдса 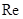при расходе, равном :

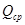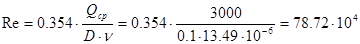
По Рис. 4. при 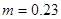для сопла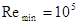

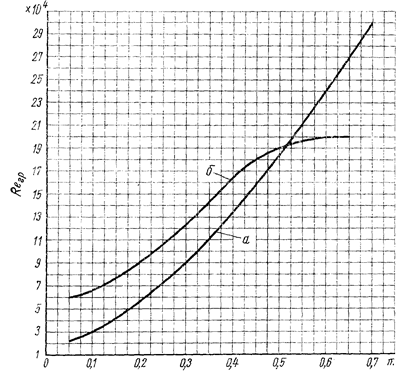
Рис. 4. Граничное число Рейнольдса:

а — диафрагмы; б — сопла и сопла Вентури

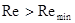, значит расчет продолжаю.

4) Определяю наибольший перепад давления 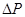в сужающем устройстве:

,

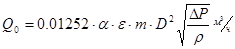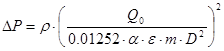
Предварительно рассчитываю поправочный множитель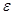

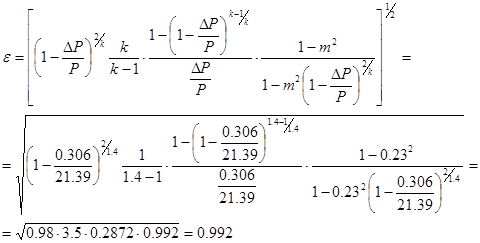
и расход 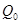сухого газа в рабочем состоянии

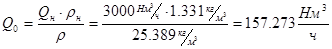
5) Подсчитываю отношение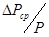

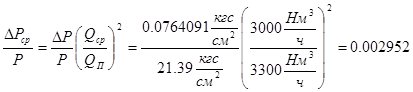
6) Определяю поправочный множитель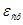

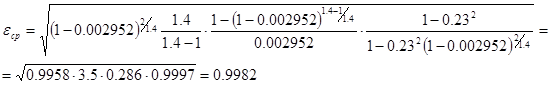
7) Подсчитываю искомое значение 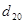диаметра отверстия сужающего устройства при 20⁰ С.

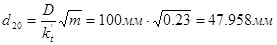
1.2 Расчет погрешности измерения расхода:

Средняя квадратичная относительная погрешность измерения расхода показывающим дифманометром определяется по формуле:

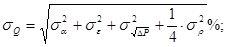
1) Средняя квадратичная относительная погрешность коэффициента расхода равна:

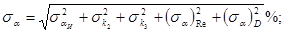
Значения 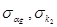нахожу на рис. 5 и 6.

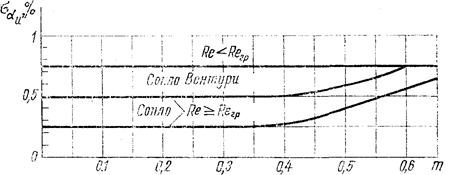
Рис. 5. Средняя квадратичная погрешность исходного коэффициента расхода сопел и сопел Вентури

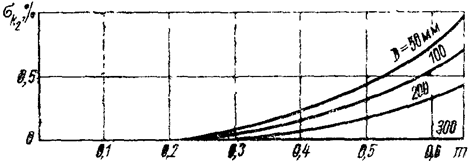
Рис. 6. Средняя квадратичная погрешность поправочного множителя на шероховатость для сопел и сопел Вентури

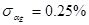
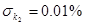
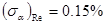- учитывает неточность поправки на влияние числа Рейнольдса или погрешность от пренебрежения этой поправкой.

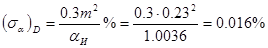
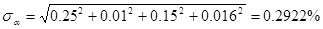
2) Рассчитываю среднюю квадратичную относительную погрешность поправочного множителя на расширение измеряемой среды:

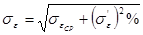
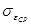- средняя квадратичная погрешность значения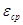

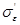- средняя квадратичная погрешность, обусловленная отклонением действительного значения 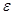от .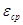

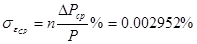, для сопла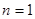

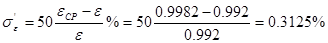
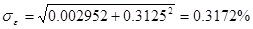
3) Если принять, что погрешность перепада давления в сужающем устройстве может быть приравнена погрешности измерения разности давлений в дифманометре, то

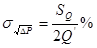
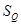- класс точности (по расходу) дифманометра;

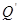- расход, выраженный в долях верхнего предела измерений дифманометра ( ).

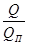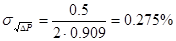
4) Рассчитываю среднюю квадратичную относительную погрешность значения плотности газа:

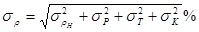
причем

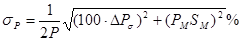
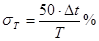
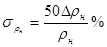
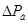- максимальная абсолютная погрешность показания барометра, кгс/см²;

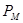- верхний предел измерений манометра, кгс/см²;

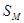- класс точности манометра;

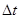- максимальная погрешность температуры, которая зависит от точности примененного термометра и условия измерения; для промышленных измерений можно принять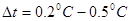

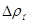- максимальная абсолютная погрешность величины 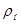, равная ½ единицы разряда последней значащей цифры в табличном значении,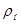

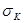- погрешность, зависящая от метода определения коэффициента сжимаемости и выбирается из таблицы 1.

Таблица 1

Газ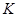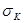
Кислород		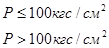0.25 0.5

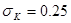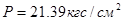
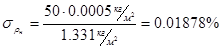
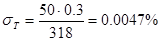, при

, при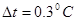

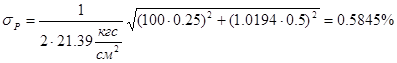
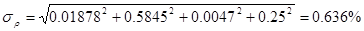
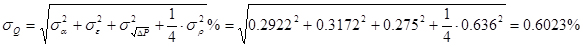
ЧЕРТЕЖ СУЖАЮЩЕГО УСТРОЙСТВА

5)

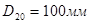
6)

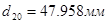
7)

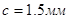
8)

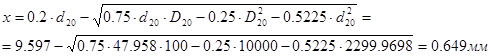
9) , , , , , , , ,

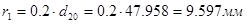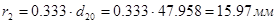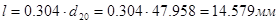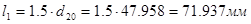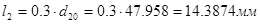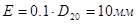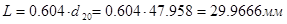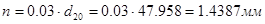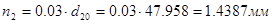
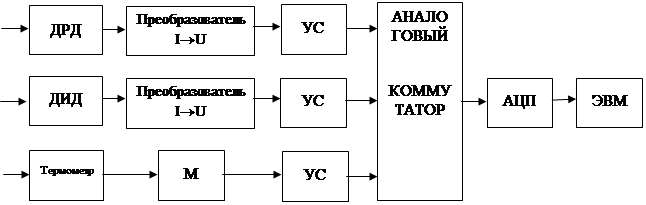
РАСЧЕТ КАНАЛОВ ИЗМЕРЕНИЯ.

В ходе анализа, был принят следующий принцип построения измерительного канала: