Примеры бинарных отношений. 6 страница

Граф отношения эквивалентности тоже имеет характерный вид. Он представляет собой граф, каждая компонента связности которого, соответствующая классу эквивалентности, является полным графом с петлями на каждой вершине. Для данного примера граф имеет вид, представленный на рис. 4.1.

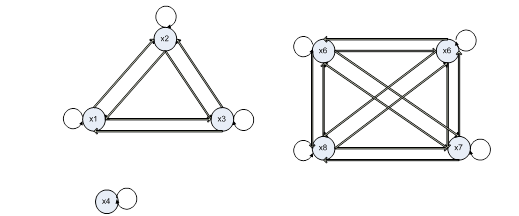
Рисунок 4.1 - Граф отношения эквивалентности

4.2.2 Отношение порядка

Определим различные варианты (типы) отношений порядка (отношение частичного, нестрого, строгого, полного, линейного порядка). Отношение порядка позволяет сравнивать между собой различные элементы одного множества.

Отношение порядка в общем случае обозначается .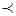

Определение

Множество, в котором определено отношение порядка, называется упорядоченным (порядок введен этим отношением).

Определение

Отношение в множестве называется отношением частичного (нестрогого) порядка, если для любых 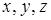из выполняются свойства:

- рефлексивности ( );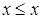

- антисимметричности (из 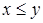и 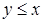следует );

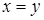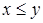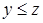- транзитивности (если и , то ).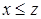

Частичный порядок принято обозначать символом 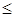, а обратное ему отношение 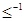принято обозначать символом .

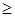Определение

Если на множестве задано отношение частичного порядка, то это множество называется частично упорядоченным.

Пример. Отношением частичного порядка в множестве людей можно назвать отношение «быть не старше» или «быть не моложе».

Отношением частичного порядка в множестве целых чисел является отношение «быть делителем» (очевидно, что не все пары элементов из множества целых чисел находятся в данном отношении)

Булеан 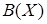, т.е. множество всех подмножеств некоторого множества , является частично упорядоченным множеством с отношением теоретико-множественного включения 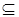, как отношения частичного порядка.

Определение

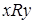Элементы и называются сравнимыми в отношении частичного порядка , если выполняется хотя бы одно из соотношений или 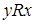. Если для некоторых пар 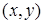ни одно из соотношени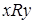й или 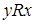не имеет места, то такие элементы называют несравнимыми.

Пример. Пусть - множество положительных делителей числа 30, а есть отношение частичного порядка ( 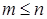), если 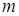делит нацело. Целые числа 5 и 15 сравнимы, поскольку 5 делит 15 нацело, а 5 и 6 - несравнимы.

Определение

Частичный порядок называется линейным (полным) порядком, если любые два элемента и из множества сравнимы, т.е. 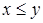и .

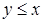Определение

Множество , на котором задано отношение частичного порядка и для которого любые два элемента этого множества сравнимы, называется линейно упорядоченным,полностьюупорядоченным или цепью.

Пример. Множество натуральных или действительных чисел с естественным отношением порядка 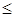, множество точек числовой оси (прямой), множество значений длин волн на шкале радиоприемника являются линейно упорядоченными.

Линейно упорядоченное (полностью упорядоченное) множество отличается от частично упорядоченного тем, что в частично упорядоченном множестве могут присутствовать элементы, из которых можно составить несравнимые пары.

Любое частично упорядоченное множество наглядно можно представить в виде схемы, которая называется диаграммой Хассе. Каждый элемент 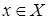на плоскости изображается точкой, и любую пару точек, соответствующих элементам 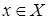и 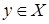, соединяют стрелкой, идущей из точки в точку , тогда и только тогда, когда 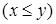, , 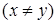и не существует 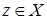такого, что 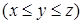, и элемент 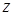отличается и от , и от .

Пример. Пусть 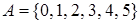- линейно упорядоченное множество с обычным отношением порядка на множестве натуральных чисел, не превосходящих пяти. Элементы этого отношения упорядочены обычным отношением частичного порядка .

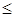Его диаграмма Хассе изображена на рис. 4.2.

Рисунок 4.2 - Диаграмма Хассе

Рассмотрим отношения нестрогого и строгого порядка.

Определение

Отношение частичного порядка, являющееся рефлексивным, антисимметричным и транзитивным, называется также отношением нестрогого порядка.

Определение

Отношение в множестве называется отношением строгого порядка(его принято обозначать символом < ), если оно:

- антирефлексивно (если 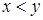, то );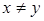

- асимметрично (если 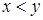, то не верно )

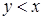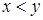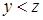- транзитивно (если и , то ).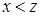

Это отношение не является частичным порядком, т.к. не удовлетворяет условию рефлексивности .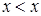

Пример. В качестве примера отношения строгого порядка можно привести отношение « 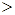» или « 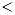» в множестве (множество натуральных чисел) или (множество действительных чисел), а также отношения «быть старше» или «быть моложе» в множестве людей.

Отношение строгого порядка характерно для различного рода иерархий с подчинением одного объекта другому (или другим)

Матрица отношения нестрогого порядка представлена следующим образом:

- главная диагональ матрицы этого отношения заполнена единицами (свойство рефлексивности);

- ни один единичный элемент не имеет симметричного себе элемента относительно главной диагонали (свойство антисимметричности);

- наличие единиц на пересечении 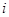-го столбца и 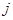-й строки, и единицы на пересечении 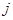-го столбца и 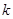-й строки, влечет за собой наличие единицы на пересечении 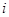-го столбца и 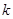-й строки (свойство транзитивности).

Матрица отношения строгого порядка отличается тем, что все элементы главной диагонали нулевые (свойство антирефлексивности).

Граф нестрогого порядка не содержит параллельных и противоположно направленных дуг, с каждой вершиной связана петля, а также все вершины любого пути попарно связаны между собой дугами в направлении этого пути.

Граф строгого порядка отличается тем, что в нем отсутствуют петли.

4.2.3 Отношение толерантности

Определение

Отношение толерантности 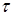на множестве удовлетворяет свойствам:

- рефлексивности ( );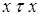

- симметричности (из 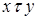следует );

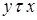- антитранзитивности .

Для этого отношения, в отличие от эквивалентности, транзитивность не обязательна, и значит, эквивалентность есть частный случай толерантности.

Отношение толерантности представляет собой формальное представление интуитивных понятий о сходстве и неразличимости. Каждый объект неразличим сам с собой (рефлексивность), а сходство двух объектов не зависит от того, в каком порядке они сравниваются (симметричность). В то же время, если один объект сходен с другим, а другой сходен с третьим, то это не означает, что все они обязательно сходны между собой, т.е. свойство транзитивности может не выполняться.

Пример.

Отношение «расстояние между двумя точками не превышает некоторого заданного числа 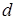» является отношением толерантности. Это значит, что толерантны любые две точки, расстояния между которыми не превышает .

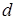На множестве кортежей (векторов) 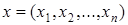толерантность можно задать различными способами, например, обусловить наличие в паре кортежей хотя бы одной общей компоненты 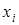. Компонентами кортежа могут быть любые объекты. Если они принимают целочисленное значение от 0 до 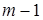, то кортеж можно рассматривать как -разрядное число, записанное в позиционной системе счисления с основанием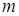

Пример. Кортеж 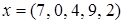соответствует десятичному числу 70492. количество всех таких кортежей, очевидно, равно .

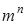При 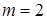имеем двоичный кортеж, его компоненты принимают значения 0 или 1. Для каждого 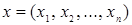существует только один не толерантный ему кортеж .

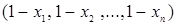Пример. Двоичный кортеж можно трактовать также как содержимое -разрядного регистра вычислительной машины. Состояние машины определяется содержимым всех его регистров, т.е. множеством двоичных кортежей. Если два состояния машины различаются содержимым некоторого ограниченного числа регистров, то говорят, что эти состояния толерантны, а машину называют толерантным автоматом.

4.3 Контрольные вопросы и задания

1. Перечислите основные свойства отношений.

2. Что такое рефлексивность отношения?

3. Какое отношение является антирефлексивным?

4. Какое отношение является симметричным?

5. Какое отношение является асимметричным?

6. Какое отношение является антисимметричным?

7. Какое отношение является транзитивным?

8. Какое отношение в множестве называется отношением эквивалентности?

9. Какое отношение в множестве называется отношением нестрогого порядка?

10. Какое отношение в множестве называется отношением строгого порядка?

11. Какое отношение называется функциональным?

Лекция 5 Функциональные отношения. Элементы реляционной алгебры

5.1 Функциональные отношения

Определение

Отношение 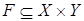называется функциональным, если его элементы (упорядоченные пары 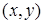) имеют различные первые координаты, т.е. каждому 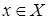либо соответствует только один элемент 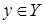, такой, что 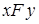, либо такого элемента вообще не существует.

Матрица функционального отношения содержит в каждой строке не более одного единичного элемента, а его граф характеризуется тем, что из каждой вершины может выходить только одна дуга (считая и петли). Элементам 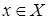, не входящим в область определения функционального отношения 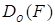, соответствует нулевой столбец в матрице и изолированная вершина в графе функционального отношения.

Пример. Пусть заданы множества 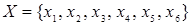и 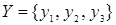. Отношение 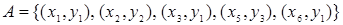является функциональным. В матрице данного отношения четвертый столбец нулевой, а его граф содержит изолированную вершину.

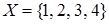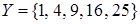Для множеств и отношение 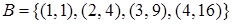, имея различные первые координаты, также является функциональным.

Всякое функциональное отношение можно рассматривать как функцию.

Определение

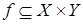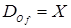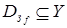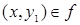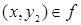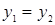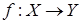Бинарное отношение называется функцией, или отображением, из множества в множество , если область определения функции , область значений функции и из , следует, что . Функция из множества в множество обозначается или .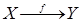

Если вместо 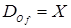выполняется 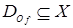, то называется частичной функцией.

Определение

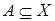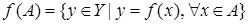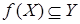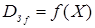Если множество , то через обозначается образ множества . Множество называется образом или областью значений отображения и обозначается . Если множество 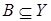, то множество 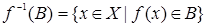называется прообразом множества относительно отображения .

Однако следует различать функцию как множество упорядоченных пар (отношение) и значение функции 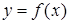как вторую координату одной из таких пар.

Для всякого функционального отношения можно определить связанную с этим отношением функцию, но симметричное к нему отношение 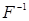может не быть функцией.

Пример. Пусть задано функциональное отношение .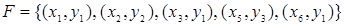

Так, отношение 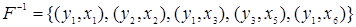, обратное рассмотренному отношению, не является функцией, так как имеют одинаковые первые координаты.

Существуют следующие основные типы отображений (функций):

- сюръекция (функция, сюръективное отображение 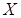на );

- инъекция (инъективная функция, инъективное отображение 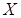на );

- биекция (биективная функция, биективное отображение 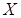на , взаимнооднозначное соответствие).

Определение

Функция 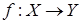называется сюръективной функцией (сюръективным отображением), если 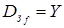. Для сюръективной функции для любого 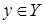существует 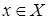такой, что .

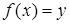На графе, представляющем сюръективное отображение 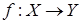, из любой вершины 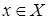выходит в точности одна дуга, а в любую вершину, представляющую элемент множества , входит не менее одной дуги.

Пример.

Сюръективное отображение 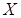на , заданное в виде графа, представлено на рис. 5.1.

Рисунок 5.1 - Сюръективное отображение 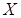на , представленное в виде графа

Определение

Функция 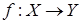называется инъективной функцией (инъективным отображением), если для любых элементов 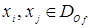из 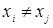следует 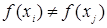(отношение 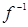является частичной функцией).

На графе, представляющем инъективное отображение 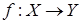, из любой вершины 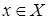выходит в точности одна дуга, а в любую вершину, представляющую элемент множества , входит не более одной дуги.

Пример.

Инъективное отображение, заданное в виде графа, представлено на рис. 5.2.

Рисунок 5.2 - Инъективное отображение 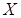на , представленное в виде графа

Определение

Функция 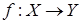называется биективной функцией (биективным отображением), если она одновременно сюръективна и инъективна.

Биективное отображение 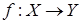осуществляет взаимнооднозначное отображение между множествами и , поэтому , .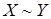

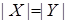Свойство биективности обеспечивает существование обратного отображения. Это означает, что если 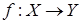биективно, то существует обратное отображение 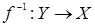, причем .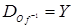