Частично-рекурсивные функции

Большинство арифметических и логических функций являются примитивно-рекурсивными. Однако класс примитивно-рекурсивных функций не охватывает всех вычислимых в интуитивном смысле функций. Для построения остальных функций используется так называемый оператор минимизации (m -оператор, оператор наименьшего корня).

Оператор минимизацииопределяет новую арифметическую функцию от n переменных с помощью ранее построенной арифметической функции от n+1 переменных. Пусть существует некоторый механизм вычисления функции , причем значение функции 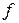неопределенно, если этот механизм работает бесконечно, не выдавая никакого определенного значения.

Зафиксируем набор значений аргументов и рассмотрим уравнение относительно y: ; чтобы найти решение этого уравнения, натуральное , будем вычислять последовательность значений:

для ..

Наименьшее целое неотрицательное значение , удовлетворяющее этому уравнению: обозначим:

.

Говорят, что функция получена из функции операцией минимизации, если:

Оператор минимизации работает бесконечно в одном из следующих случаев:

1) значение не определено;

2) значение для определены, но не равны нулю, а значение – не определено;

3) значение определены для всех , но не равны нулю.

Пример 13. Процесс вычисления функции с помощью оператора минимизации:

Пример 14. Оператор минимизации является удобным средством получения обратных функций: вычитание, деление, извлечение корня и т.д.:

.

.

.

.

Частично-рекурсивная функция – функция, которая может быть построена из простейших с помощью конечного числа применений оператора суперпозиции, примитивной рекурсии и минимизации.

Частично-рекурсивная функция является не всюду определенной, причем там, где она не определена, процесс ее вычисления продолжается бесконечно.

Общерекурсивная функция–всюду определенная частично-рекурсивная функция.

Связь между алгоритмами и рекурсивными функциями выражается тезисом Черча: какова бы ни была вычислимая неотрицательная целочисленная функция от неотрицательных целочисленных аргументов, существует тождественно равная ей частично-рекурсивная функция.

Класс частично-рекурсивных функций (ЧРФ) шире чем класс общерекурсивных функций (ОРФ), который в свою очередь шире классса примитивно-рекурсивных функций (ПРФ) (см. рис. 1).

Рисунок 1 – Соотношение между классами частично-рекурсивных, общерекурсивных и примитивно-рекурсивных функций

Задание на лабораторную работу

1. Разработать алгоритм вычисления в виде рекурсивной функции.

2. Проверить модель алгоритма на множестве тестовых примеров.

3. Определить к какому классу рекурсивных функций принадлежит : примитивно-рекурсивна, частично-рекурсивна или общерекурсивна.

Варианты заданий

1. Сумма всех четных делителей числа .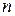

2. Количество всех нечетных делителей числа .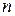

3. Количество нулей в двоичной записи .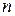

4. Сумма цифр в двоичной записи .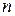

5. Количество взаимно-простых с 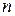чисел,

6. Максимальная цифра в 8-ричной записи числа .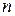

7. Минимальная цифра в 8-ричной записи числа .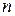

8. Количество четных цифр в 8-ричной записи числа .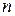

9. Количество нечетных цифр в 8-ричной записи числа .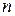

10. Сумма простых делителей числа .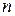

11. Количество простых делителей числа .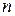

12. Количество простых чисел,

13. Количество чисел, являющихся полными квадратами,

14. Сумма чисел, являющихся степенью двойки,

15. Максимальная цифра в 16-ричной записи числа .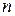

16. Минимальная цифра в 16-ричной записи числа .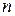

17. Ближайшее к 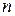простое число.

18. Произведение делителей числа .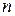

19. Произведение простых делителей числа .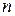

20. Произведение взаимно-простых с 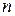чисел,

21. Наименьшее общее кратное двух чисел, ,

22. Наибольший общий делитель двух чисел,

23. Функция, отличная от нуля в конечном числе точек.

24. Номер наибольшего простого делителя числа

25. Функция, вычисляющая целую часть квадратного корня от аргумента, .

Контрольные вопросы

1. Что такое вычислимая, арифметическая, частичная или всюду определенная функция?

2. Определить операторы суперпозиции и примитивной рекурсии.

3. Перечислить простейшие функции теории рекурсивных функций.

4. Что такое примитивно-рекурсивные функции?

5. Показать примитивную рекурсивность известных арифметических функций.

6. Показать примитивную рекурсивность арифметизованных логических функции. Примитивная рекурсивность отношений и предикатов.

7. Определить оператор минимизации, в каких случаях он работает бесконечно?

8. Что такое частично-рекурсивная функция и общерекурсивная?

9. Сформулировать тезис Черча.

10. Определите соотношение между примитивно, частично и общерекурсивными функциями.

Лабораторная работа № 2

МАШИНЫ ТЬЮРИНГА

Цель работы: получить практические навыки в записи алгоритмов с использованием машин Тьюринга.

Теоретическая справка

Символьные конструкции

Алфавитомбудем называть любое конечное множество попарно различных знаков, называемых буквами (символами) этого алфавита. Алфавит будем обозначать заглавными буквами, например:

Символом l будем обозначать пустой символ.

Словомв данном алфавите называется любая конечная (в том числе и пустая) последовательность букв этого алфавита. Слова будем обозначать малыми греческими буквами.

Например: a = алгоритм – слово в алфавите А; b = 1010100 – слово в алфавите В; – слово в алфавите С.

Пустое слово будем обозначать L.

Длинаслова a (обозначается ) – это количество букв в слове.

Определим некоторые отношения и операции над словами.

Равенство словв алфавите А определяется индуктивно:

а) пустые слова равны

б) если слово a равно слову b, то a b =bb , где b –буква в алфавите А.

Если слово a является частью слова b, то говорят, что имеет место вхождениеслова a в слово b (слово a называется подсловом слова b). Это можно записать следующим образом: , где – слова в алфавите А.

Слово a называется началом слова b, если ; концомслова b, если . Слово длины n, составленное из буквы а, повторенной n раз, будем обозначать , например xyxxxyyyy = .

Операция (и результат) приписывания слов a и b друг к другу называется конкатенацией(обозначается a||b). Например, если .

Определение машины Тьюринга (МТ)

Под машиной Тьюринга понимается некоторая гипотетическая (абстрактная) машина, состоящая из следующих частей:

1) бесконечной в обе стороны ленты, разбитой на ячейки, в каждой из ячеек может быть записан только один символ из алфавита , а также пустой символ l;

2) рабочей головки или управляющего устройства (УУ), которое в каждый момент времени может находиться в одном из состояний множества . В каждом из состояний головка размещается напротив ячейки и может считывать (обозревать) или записывать в нее букву из алфавита А.

Машина Тьюринга

Функционирование МТ состоит из последовательности элементарных шагов (тактов). На каждом шаге выполняются следующие действия:

1) управляющее устройство считывает (обозревает) символ ;

2) в зависимости от своего состояния и обозреваемого символа

УУ вырабатывает символ и записывает его в обозреваемую ячейку (возможно );

3) головка перемещается на одну ячейку вправо (R), влево (L) или остается на месте (E);

4) головка переходит в другое внутреннее состояние (возможно ).

Состояние называется начальным, – заключительным. При переходе в заключительное состояние машина останавливается.

Полное состояние МТ называется конфигурацией. Это распределение букв по ячейкам ленты, состояние рабочей головки и обозреваемая ячейка. Конфигурация в такте t записывается в виде: , где – подслово слева от обозреваемой ячейки, – буква в обозреваемой ячейке, – подслово справа. Начальная конфигурация и конечная называются стандартными.

Для описания работы МТ существует 3 способа:

1) система команд вида

2) функциональная таблица;

3) граф (диаграмма) переходов.

С помощью МТ можно описывать выполнение арифметических операций над числами. При этом числа представляются на ленте, как слова в алфавите, состоящем из цифр какой-нибудь системы счисления, и разделяющихся специальным знаком, не входящем данный алфавит, например, .

Наиболее употребительной является унарная система, состоящая из одного символа – . Число Х в унарной системе счисления на ленте записывается словом , ( сокращенно ) в алфавите А={ }.

Пример 1. Операция сложения двух чисел в унарном коде.

Начальная конфигурация: . Конечная конфигурация: , т.е. сложение фактически сводится к приписыванию числа b к числу a . Для этого первый символ стирается, а * заменяется на .

Система команд при и .

Комментарий к системе команд

1. – стирание первого символа .

Если в обозреваемой ячейке записан символ и МТ находится в состоянии _, тогда состояние изменяется на , обозреваемый символ заменяется на пустой, УУ сдвигается вправо.

2. – стирание символа , первый аргумент равняется 0.

Если в обозреваемой ячейке записан символ и МТ в состоянии (первый аргумент равняется 0)_, тогда состояние изменяется на , обозреваемый символ заменяется на пустой, УУ сдвигается вправо.

3. – сдвиг вправо.

Если в обозреваемой ячейке записан символ, записан символ и МТ находится в состоянии _, тогда состояние и обозреваемый символ не изменяются, УУ сдвигается вправо.

4. – стирание символа .

Если в обозреваемой ячейке записан символ и МТ находится в состоянии _, тогда состояние изменяется на , и обозреваемый символ заменяется на , УУ сдвигается влево (конец первого аргумента).

5. – сдвиг влево.

Если в обозреваемой ячейке записан символ и МТ находится в состоянии , тогда состояние и обозреваемый символ не изменяются, УУ сдвигается влево.

6. – конец алгоритма, останов.

Если в обозреваемой ячейке записан символ и МТ находится в состоянии _, тогда состояние изменяется на , обозреваемый символ не изменяется, УУ сдвигается вправо (конец алгоритма, УУ расположено в начале рабочей зоны ).

Описание МТ в виде функциональной таблицы:

	|	*	l
			-
			-
		-

Описание МТ в виде диаграммы переходов

Вычисление на МТ словарной функции будем понимать следующим образом. Пусть в начальной конфигурации на ленте записано слово 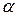. Если значение определено, то конечного числа шагов (тактов) машина должна перейти в заключительную конфигурацию, в которой на ленте записано слово . В противном случае МТ должна работать бесконечно.

Числовая функция правильно вычислима (или просто вычислима) по Тьюрингу, если существует МТ, которая переводит конфигурацию в конфигурацию , когда =y , или работает бесконечно, когда не определена.

Задание на лабораторную работу

1.Описать системой команд, функциональной таблицей и диаграммой переходов работу машины Тьюринга, реализующую заданный вариантом алгоритм. Начальная и конечная конфигурации стандартны.

2. Проверить модель алгоритма на множестве тестовых примеров. Привести последовательности конфигураций машины Тьюринга, заданной в предыдущем пункте, для различных тестовых исходных слов.

Варианты заданий

1. Реализовать функцию арифметическое вычитание 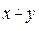в унарном коде.

2. Реализовать функцию выбор максимального из двух чисел над числами в унарном коде.

3. Реализовать функцию над числами в унарном коде.

4. Реализовать функцию 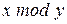над числами в унарном коде.

5. Реализовать функцию 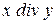над числами в унарном коде.

6. Реализовать функцию 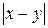над числами в унарном коде.

7. Реализовать функцию выбор аргумента 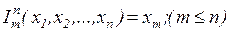над числами в унарном коде.

8. Реализовать вычисление предиката X>Y в унарном коде с сохранением (восстановлением) исходных данных.

9. Реализовать вычисление предиката X=Y в унарном коде с сохранением (восстановлением) исходных данных.

10. Реализовать вычисление предиката “x - четное число” в двоичном коде.

11. Реализовать алгоритм в алфавите 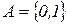, меняющий местами первую и последнюю буквы слова.

12. Реализовать алгоритм над алфавитом 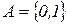, меняющий местами первый ноль и последнюю единицу.

13. Реализовать операцию копирование в алфавите 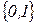, то есть получить из слова 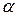слово .

14. Реализовать алгоритм над алфавитом 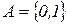, который выдает единицу, если в исходном слове только парные нули и ноль в противном случае.

15. Реализовать алгоритм в алфавите 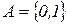, который переставляет буквы в слове 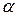так, чтобы сначала шли все нули, потом – единицы.

16. Реализовать алгоритм, конструирующий в алфавите 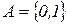слова вида , где 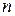- произвольное натуральное число.

17. Реализовать алгоритм, реализующий функцию циклический сдвиг двоичного числа на одну ячейку.

18. Реализовать алгоритм в алфавите 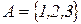, анализирующий последовательность цифр в слове и выдающий «+», если цифры образуют неубывающую последовательность, и «–» в противном случае.

19. Реализовать выделение подстроки, заключенной между двумя символами (первая пара) в алфавите . Если последовательность отсутствует на ленте, стереть все.

20. В слове 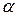в алфавите 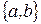стереть все, кроме 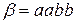. Если такой последовательности нет, все стереть.

21. Реализовать алгоритм над алфавитом 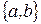, переставляющий буквы в обратном порядке.

22. Реализовать предиката «в слове a в алфавите есть пара букв ‘yy’ » .

23. Реализовать алгоритм в алфавите , производящий в слове a алфавита замену всех вхождений буквы а на букву б.

24. Реализовать алгоритм в алфавите 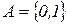для вычисления логической функции , где x,y,z принимают значение 0 или 1.

25. Реализовать алгоритм в алфавите 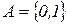для вычисления логической функции , где x,y,z принимают значение 0 или 1.

Контрольные вопросы

11. Дать определение машины Тьюринга и ее составляющим.

12. Перечислить и определить способы описания МТ.

13. Какие операции выполняются в каждом такте работы МТ?

14. Дать определение конфигурации МТ.

15. Какие начальные и конечные конфигурации называют стандартными и как они обозначаются?

16. Что такое функция, правильно вычислимая по Тьюрингу?

17. Какие способы композиции МТ существуют, как они применяются и обозначаются?

18. Формулировка тезиса Тьюринга; можно ли его доказать строго?

Лабораторная работа № 3

КОМПОЗИЦИЯ МАШИН ТЬЮРИНГА

Цель работы: получить практические навыки в записи алгоритмов с использованием композиции машин Тьюринга.

Теоретическая справка

Вышеперечисленные способы описания МТ практически можно использовать только для несложных алгоритмов, в противном случае описание становится слишком громоздким. Машины Тьюринга для сложных алгоритмов могут строиться с использованием уже имеющихся элементарных МТ и такое построение называется композицией МТ.

Опишем 4 основных способа композиции МТ:

- последовательная композиция ( суперпозиция );

- параллельная композиция;

- разветвление

- цикл