Коэффициент направленного действия и его свойства

ОСНОВЫ ЭНЕРГЕТИЧЕСКОЙ ТЕОРИИ ИНТЕРФЕРЕНЦИОННЫХ СИСТЕМ

Учебное пособие

Саратов

1990 г.

- 2 -

Содержание

Введение …………………………………………………………………………. 3

1. Основные положения ………………………………………………………… 4

2. Коэффициент направленного действия и его свойства ……………………. 8

3. Расчет КНД интерференционных систем …………………………………… 11

4. Анализ xaрактеристик интерференционных систем по графикам КНД ….. 14

Контрольные вопросы ………………………………………………………….. 17

- 3 -

ВВЕДЕНИЕ

Известно, что регистрируемая в сейсморазведке информация может быть условно (в соответствии с условиями конкретной задачи) разделена на полезную и помехи. Полезная информация представляет из себя запись регулярных волн, образовавшихся на исследуемых границах. Помехи в свою очередь могут быть как регулярными , так и нерегулярными (случайными). Понятие случайной волны также является условным. Под ними следует понимать регулярные волны, запаздывания одноименных фаз которых в соседних точках регистрации превышают радиус их корреляции.

Известно также, что полезная является лишь весьма небольшой частью общего объема информации, регистрируемой на сейсмограммах. Поэтому задача выделения и интерпретации ее является основной задачей сейсморазведки. Основой выделения полезной информации может служить ее регулярность, другими словами – априорное знание характера распределения полезных сигналов во времени - пространстве. Характер распределения описывается функциональной зависимостью вида t = t(x,y,z), где x, y, z, -- пространственные координаты точки регистрации. Эта зависимость характеризует кинематические особенности (характеристики) волны.

Разделение полей полезных волн и волн-помех (т.е. выделение полезных и подавление помех) осуществляется так называемыми интерференционными системами, основанными, главным образом, на суммировании сейсмических колебаний, зарегистрированных в разных точках пространства, с учетом кинематических характеристик выделяемых и подавляемых волн. При этом обеспечивается синфазное сложение выделяемых колебаний и несинфазное – подавляемых.

Количественное описание свойств таких систем дается в рамках их теории. В настоящее время получили распространение частотная и энергетическая теории интерференционных систем. Первая рассматривает процесс суммирования сейсмических колебаний в пространственно-частотной области. Она весьма удобна для анализа свойств конкретных систем и позволяет; единообразно описывать многие процедуры регистрации и обработки сейсмической информации. Энергетическая теория описывает процесс суммирования в более привычной пространственно-временной области и несколько удобнее для. синтеза интерференционных систем. Между обеими теориями в идеальном случае могут быть установлены количественные соотношения.

Ввиду того, что главной задачей университетских курсов является ознакомление студентов с выбором конкретной методики решения геологических задач сейсморазведочными методами (выбор метода, синтез полевой системы наблюдений и определения процедур обработки), представляется целесообразным рассмотреть работу интерференционных систем с точки зрения энергетической теории.

- 4 -

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Теория интерференционных систем описывает интерференции сейсмических волн при распространении их в среде или интерференцию сигналов, порожденных ими. Ввиду того, что реальные среды и определяемые ими волновые поля очень сложны, теория рассматривает поле идеально-регулярных волн.

Под идеально-регулярными волнами понимаются плоские волны, распространяющиеся в бесконечном полупространстве без затухания.

Сигналы, вызываемые ими ж в разных точках пространства, отличается лишь параметром времени. Однако при описании сложных интерференционных систем, примером которых может служить способ общей глубинной точки, возникает необходимость усложнения как модели среды, так и волнового поля: предполагается, что сферические волны распространяются в среде, аппроксимируемой среднескоростной моделью, без затухания. На форму же сигналов сейсмического импульса существенных ограничений не накладывается. Из всего сказанного выше видно, что этот подход является расширением лучевого представления волнового поля.

Под интерференционной системой будем понимать систему суммирующую некоторую совокупность сигналов, поступающую на ее входы.

Такой совокупностью может быть система сейсмических волн, подходящих к сейсмоприемнику, совокупность сигналов от нескольких сейсмоприемников, суммирующаяся на входе сейсмического усилителя, совокупность отсчетов с нескольких файлов записи, суммируемая интерференционной системой будем понимать систему сумми­рующую некоторую совокупность сигналов, поступающую на ее входы. В первом случае в качестве интерференционной системы может выступать и группа источников сейсмических колебании в сочетании со средой их распространения, где волны, вызываемые каждым из источников, распространяются в соответствии с принципом суперпозиции. Суммирующим элементом в этом случае является сейсмоприемник.

Интерференционные системы можно подразделить на дискретные -обладающие конечным количеством входов с чувствительностью µ_i , где i - номер входа, и непрерывные, имеющие бесконечное количество входов, с плотностью распределения чувствительности µ’_x, где х – координата входа системы. Непрерывные интерференционные системы были лишь полезной абстракцией до появления непрерывных источников колебаний типа линий детонирующего шнура.

Независимо от природы интерференционной системы, как правило, ее можно свести к совокупности входов (источников сигналов), располагающихся на плоскости наблюдения, каждый из которых может быть охарактеризован координатами, определенными на этой плоскости, и чувствительностью (интенсивностью). По характеру расположения входов на плоскости наблюдения интерференционные системы можно подразделить на линейные, где входы располагаются вдоль некоторой линии, и площадные.

- 5 -

В зависимости от характера распределения; чувствительности можно рассматривать однородные системы, где чувствительность не зависит от координат входа, и неоднородные.

В дискретных линейных интерференционных системах кроме того выделяют равномерные, где расстояние между соседними входам является величиной постоянной, и неравномерные.

Под базой интерференционной системы по некоторому направлению α на плоскости наблюдения (D_α) - см. рис .1 - расстояние между максимально удаленными друг от друга проекциями входов интерференционной системы на это направление.

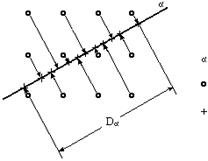
Рис.1 База интерференционной
системы по направлению.

– направление на плоскости
наблюдения ;

– входы интерференционной
системы;

– проекции входов на напра
вление α

В линейных интерференционных системах под базой группы обычно понимают расстояние между крайними входами этой системы (D). Для дискретных линейных систем справедливо равенство:

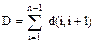(1)

где d(i,i+1) – расстояние между i – тым и i+1 входами системы.

В линейных равномерных группах:

D=(n-1)d (2)

Необходимая степень подавления волны-помехи, интерферирующей с полезными волнами, может быть выражена

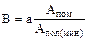(3)

где B -необходимая степень ослабления волны-помехи;
A_пом – среднее значение амплитуды волны-помехи;
А_{пол(мин)} – среднее значение амплитуды самой слабой полезной волны

интерферирующей с рассматриваемой помехой;

- 6 -

a – коэффициент, определяемый требуемым качеством ослабления
волны-помехи (при α=2÷3 – ослабление удовлетворительное,
при a = 8÷1О –хорошее).

В начале рассмотрения основ теории интерференционных систем ограничимся случаем распространения плоских волн в однородной сре­де типа "полупространство". Реальные волны могут, быть аппроксимированы подобным образом лишь на ограниченных участках областей их существования, а именно там, где квзисферические волновые фронты незначительно отклоняются от аппроксимирующих плоскостей. По мере усложнения задач, стоявших перед интерференционными системами, будем усложнять как волновое поле, так и рассматриваемые модели сред.

Предположим, что некоторая волна на плоскости наблюдения, описываемой уравнением z=0, в точке с координатами (х=0,y=0) создает сигнал f(t) . Тогда в произвольной точке (х.у) сигнал можно представить как:

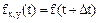(4)

где ,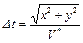

V* – кажущаяся скорость этой волны ( V* =const (x,y) в силу того , что
фронт рассматриваемой волны - плоский).

Сигнал на выходе пространственной непрерывной системы определится равенством:

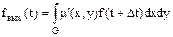(5)

где G – площадь, занимаемая интерференционной системой на плоскости
наблюдения;

µ'(x,y) – плотность распределения чувствительности внутри этой площади.

Для дискретной интерференционной системы выражение (5) преобразуется к виду:

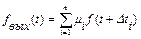(6)

где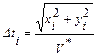

µ¡ – чувствительность i-того входа системы (1≤ i ≤ n, где n – количество
входов).

- 7 -

Для линейных систем, ориентированных по оси абсцисс, выражения (5) и (6) запишутся так:

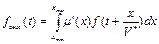(7)

где x_min, x_max– координаты концов линейной системы;

µ'(x) – плотность распределения чувствительности при x_min ≤x ≤ x_max;

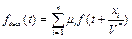(8)

Для линейных равномерных систем равенство (8) можно записать:

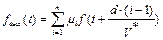
где d – расстояние между соседними входами.

Согласно определенно энергия сигнала выражается равенством:

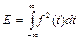(9)

Рассмотрим теорию интерференционных систем только в приложении к дискретным системам. Возможность такого ограничения основана на том, что формулы, справедливые для дискретного случая с помощью предельного перехода достаточно просто трансформируются для непрерывных систем. Кроме того, сами непрерывные интерференционные системы в настоящее время обладают ограниченными возможностями и представлены лишь непрерывным- источником на базе линий детонирующего шнура. У таких систем можно изменять лишь два параметра: мощность и величину базы. Выбор второго пара­метра для дискретного и непрерывного источника осуществляется совершенно одинаково, подбор же оптимальной мощности источника в любом случае производится эмпирически.

- 8 -

КОЭФФИЦИЕНТ НАПРАВЛЕННОГО ДЕЙСТВИЯ И ЕГО СВОЙСТВА

В основу энергетической теории интерференционных систем положено рассмотрение свойств одномерных (линейных). В практике работ они используются наиболее часто. Получить представление о свойствах двумерных (площадных) систем можно, сводя их к одномерным системам.

Сигнал на выходе дискретной интерференционной системы, имеющей n входов с чувствительностью µ¡, зависящей от номера. входа, может быть записан как 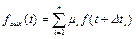(10)

где f(t) – сигнал в точке с координатами х=0 , у=0;

Δt¡ – запаздывание сигнала в точке с координатами x_i, y_i по отношению
к началу координат.

Энергия сигнала на выходе системы, согласно выражению (9), будет:

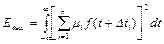(11)

Нетрудно видеть, что для знакопеременного импульса, какими и являются сейсмические сигналы, максимальная энергия на выходе интерференционной системы реализуется при Δt¡ = const, т. е. при синфазном сложении колебаний. Тогда: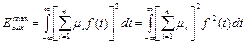

Или: 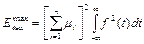(12)

Коэффициентом направленного действия ( КНД) интеренференционной системы будем называть отношение энергии сигнала некоторой волны на выходе интеренференционной системы к максимально возможной энергии выходного сигнала той же волны в той же системе:

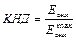
КНД характеризует степень ослабления волны за счет действия интеренференционной системы с входами, размещенными в разных точках плоскости наблюдения и обладающими чувствительностью µ¡. Максимально возможную энергию сигнала той же волны можно получить, собрав все входы этой системы в одну точку.

- 9 -

Рассмотрим более детально выражение для КНД:

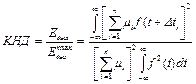(13)

Разложим квадрат суммы в числителе:

КНД = 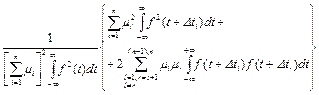(14)

Первое слагаемое в фигурных скобках есть сумма квадратов сигналов с каждого входа, второе – удвоенная сумма их попарных произведений. Анализ полученного выражения (14) позволяет выявить свойства КНД.

1. Максимальное значение КНД достигается при синфазном суммировании сигналов f(t), когда Δt = 0.При этом числитель становится равным знаменателю, а КНД _max =1.

2. Можно показать, что для знакопеременного импульса и не знакопеременной чувствительности входов системы (знакопеременное распределение чувствительности в практике работ реализуется исключительно редко) первое слагаемое в фигурных скобках в выражении (14) всегда больше второго. Из этого следует, что КНД > 0 во всем диапазоне изменения его аргументов, и что интерференционные системы не могут подавить помехи полностью.

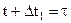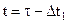3. Интеграл, стоящий под знаком удвоенной суммы , можно рассматривать как функцию автокорреляции импульса f(t). Действительно, если произвести замену одной из переменных функции, например , то , а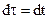
Тогда 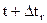можно представить как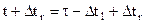

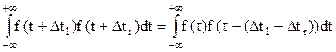
При значениях запаздывания сигналов на входах интеренференционной

системы, превышающих длительность импульса функция автокорреляции обращается в ноль. КНД становится величиной постоянной и равной:

- 10 -

КНД = 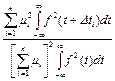(15)

При бесконечных пределах интегрирования интегралы в числителе и знаменателе равны и КНД = 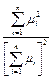= const (16)

В частном случае одно родной интерференционной системы, где КНД = I/n

Из этого следует, что статистический выигрыш такой системы по энергии и ам­плитуде соответственно равен 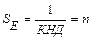, 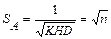(17)

В качестве аргумента функции КНД обычно используется безразмерное выражение Dt / T, где Dt -величина максимального запаздывания в пределах рассматриваемой интерференционной системы, т.е.

,

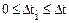а Т – величина преобладающего (видимого) периода импульса. Так как на
практике чаще всего используются равномерные интерференционные системы, то 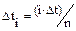, где I = 0, 1 ,2,…,(n-1)

Иногда в качестве аргумента используется выражение D/l^*, .где D – база интерференционной системы , l* – кажущаяся- длина волны. Оба эти аргумента тождественны друг другу, что легко показать на примере равномерной системы:

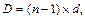
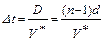, то-есть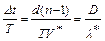

График КНД абстрактной интерференционной системы можно представить в виде кривой (см. рис. 2)_, имеющей максимум при Dt/T=0, ряд локальных минимумов и максимумов, причем любое минимальное значение КНД >0 . При Dt/T > τ _имп /T ( здесь τ_имп - длительность импульса сигнала) кривая КНД стабилизируется на уровне , определяемым выражением (16).

Количество локальных минимумов и максимумов зависят от числа периодов в импульсе сигнала, глубина их – от распределения чувствительности.

- 11 -

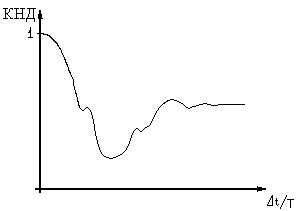
Рис 2 График КНД