Умножение двоичных чисел с плавающей запятой

Умножение чисел, представленных в форме с плавающей запятой, выполняется за четыре шага.

1. Определяется знак произведения путем сложения по модулю два знаков сомножителей.

2. Определяется порядок произведения путем алгебраического сложения (с учетом знаков) порядков сомножителей по правилам сложения чисел с фиксированной запятой.

3. Определяется мантисса произведения путем умножения мантисс сомножителей по изложенным выше правилам для чисел с фиксированной запятой.

4. Нормализуется результат умножения мантисс сомножителей, если произошла денормализация.

Пример.

Множимое .

Множитель .

Требуется найти т.е. найти и .

Первый шаг.Определение знака произведения:

.

Второй шаг.Определение порядка произведения путем сложения порядков сомножителей в модифицированном дополнительном коде:

+

не учитывается

Третий шаг.Определение модуля мантиссы произведения │m_x│х│m_y│=│m_z│:

x

+

Ограничивая результат шестью разрядами, имеем ненормализованное значение модуля мантиссы произведения .

Четвертый шаг.Нормализация результата умножения мантисс сомножителей путем сдвига модуля мантиссы произведения на один разряд влево и уменьшения порядка на единицу:

.

Результат операции умножения :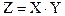

.

Методы ускоренного выполнения операции умножения

Двоичных чисел

По данным статистики, при выполнении инженерных и экономических расчетов из общего количества операций, выполняемых ЭВМ, на долю умножения приходится 30 % и более. В связи с тем, что на выполнение операции умножения тратится значительно больше времени, чем на логические операции и операцию сложения (вычитания), то в общем балансе времени доля, приходящаяся на умножение, оказывается еще более высокой. Поэтому ускорение выполнения операции умножения существенным образом сказывается на увеличении производительности ЭВМ.

На практике нашли применение различные методы ускорения выполнения операции умножения, которые можно разделить на логические, аппаратурные и комбинированные аппаратурно-логические методы.

Под логическими понимаются методы ускорения выполнения операции умножения, связанные в основном с некоторым усложнением схемы управления и не приводящие практически к изменению общей структуры арифметического устройства.

Под аппаратурными понимаются методы, связанные с существенным увеличением аппаратурного состава арифметического устройства и изменением его общей первоначальной структуры. Аппаратно-логические методы занимают промежуточное положение.

Логические методы ускоренного выполнения операции умножения делятся на две группы:

- методы, позволяющие уменьшить количество суммирований в процессе умножения;

- методы, позволяющие за один цикл умножения обработать несколько разрядов множителя путем некоторого усложнения схемы и введения в регистры дополнительных цепей сдвига.

Последние из указанных методов можно разделить на синхронные и асинхронные. Синхронные методы характеризуются тем, что в каждом цикле умножения обрабатывается фиксированное число (два и более) разрядов множителя, то есть длина цикла умножения постоянная.

При реализации асинхронных методов ускорения операции умножения количество разрядов множителя, обрабатываемых в каждом цикле умножения, зависит от комбинации разрядов множителя, анализируемых в данном цикле, то есть длина цикла умножения переменная.

Аппаратурные методы ускоренного выполнения операции умножения делятся на следующие группы:

- схемотехнические методы ускорения выполнения операций сложения и сдвига;

- метод, основанный на использовании при выполнении операции умножения прямого вычитания;

- метод, основанный на введении дополнительных цепей сдвига, позволяющих за один такт производить сдвиг информации в регистрах на несколько разрядов;

- схемотехнический метод совмещения по времени операций сложения и сдвига.

Ускорение выполнения операции сложения обычно достигается увеличением скорости работы логических элементов и триггеров, а также ускорением распространения переносов.

Для одновременной обработки нескольких разрядов множителя за один цикл умножения в регистры вводят дополнительные цепи, предназначенные для сдвига множителя и частичных произведений (или множимого) сразу на такое количество разрядов, сколько обрабатывается в данном цикле умножения.

Совмещение по времени операций сложения и сдвига может быть достигнуто соответствующим усложнением схемы сумматора. Введением дополнительных схем передачи результата суммирования в регистр суммы можно совмещать сложение со сдвигом одновременно на несколько разрядов.

В данном учебном пособии рассматриваются только логические методы ускоренного выполнения операции умножения.

Логические методы ускоренного выполнения операции умножения чаще всего применяются в арифметических устройствах параллельного действия. При этом наиболее широко используются метод пропуска такта суммирования, метод анализа сомножителей для определения сомножителя (множителя) с наименьшим числом единиц, метод расшифровки и одновременного умножения на два и более разрядов множителя и другие. Рассмотрим некоторые из этих методов.