Моделирование разностных методов в среде MATLAB
%Глобальная реализация метода нечеткого маскирования
clear;
fid=fopen('F:\MATLAB\gory.img','r');
[A,count]=fread(fid,'char');
fclose(fid);
M=input(' M=');
N=input(' N=');
A=A(9:length(A));
A=A(1:N*M);
L=reshape(A,N,M);
k=2;
LS=mean(mean(L));
Lvyh=LS+k.*(L-LS);
for i=1:N;
disp(i);
for j=1:M;
if Lvyh(i,j)>255; Lvyh(i,j)=255;
end;
if Lvyh(i,j)==0; Lvyh(i,j)=0; end;
end;
end;
Lvyh=round(Lvyh);
fid=fopen('F:\MATLAB\unshr2.img','wb');
count=fwrite(fid,Lvyh,'char');
fclose('all');
colormap(gray(255));
subplot(221);
image(L');
subplot(222);
image(Lvyh');
 а) исходное изображение |  б) изображение а, обработанное глобальным методом нечеткого маскирования при к=1,1 |
 в) изображение а, обработанное глобальным методом нечеткого маскирования при к=1,5 |  г) изображение а, обработанное глобальным методом нечеткого маскирования при к=2 |
Рис. 1. Глобальная реализация метода нечеткого маскирования.
Из рис. 1 видно, что увеличение коэффициента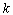 
приводит к увеличению контрастности изображения. Возможна также скользящая реализация метода (рис.2).
clear;
fid=fopen('F:\MATLAB\gory.img','r');
[A,count]=fread(fid,'char');
fclose(fid);
M=input('M=');N=input('N=');
A=A(9:length(A));
A=A(1:N*M);
L=reshape(A,N,M);
m=15;n=15;n1=fix(n/2);m1=fix(m/2);
a=L(1,1);b=L(1,M);c=L(N,1);d=L(N,M);
for i=1:n1;
for j=1:m1;
L1(i,j)=a; L3(i,j)=b; L6(i,j)=c; L8(i,j)=d;
end;
end;
L2=L(1,1:M); L02=L2;
for i=1:n1-1;
L2=[L2;L02];
end;
L7=L(N,1:M); L07=L7;
for i=1:n1-1;
L7=[L7;L07];
end;
L4=L(1:N,1); L4=L4'; L04=L4;
for i=1:m1-1;
L4=[L4;L04];
end;
L4=L4'; L5=L(1:N,M); L5=L5';
L05=L5;
for i=1:m1-1;
L5=[L5;L05];
end;
L5=L5'; L1=[L1;L4]; L1=[L1;L6]; L1=L1'; L2=[L2;L]; L2=[L2;L7];
L2=L2'; L3=[L3;L5]; L3=[L3;L8]; L3=L3'; L1=[L1;L2]; L1=[L1;L3]; Lroshyrena=L1';
clear L2;clear L3;clear L4;clear L5;clear L6;clear L7;clear L8;
clear L02;clear L04;clear L05;clear L07;clear L1;clear L;
k=2;
for i=1+n1:N+n1;
disp(i)
for j=1+n1:M+m1;
if j==1+m1;
D=0;
for a=-n1:n1;
for b=-m1:m1;
D(n1+1+a,m1+1+b)=Lroshyrena(i+a,j+b);
end;
end;
end;
if j>1+m1;
for a=-n1:n1;
D(n1+1+a,m+1)=Lroshyrena(i+a,j+m1);
end;
D=D(1:n,2:m+1);
end;
LS=mean(mean(D));
Lvyh(i,j)=LS+k.*(Lroshyrena(i,j)-LS);
if Lvyh(i,j)>255;
Lvyh(i,j)=255;
end;
if Lvyh(i,j)==0;
Lvyh(i,j)=0;
end;
end;
end;
Lvyh=round(Lvyh);
Lvyh=Lvyh(1+n1:n1+N,1+m1:m1+M);
L=Lroshyrena(1+n1:n1+N,1+m1:m1+M);
fid=fopen('F:\MATLAB\ unshrl4.img','wb');
count=fwrite(fid,Lvyh,'char');
fclose('all');
colormap(gray(255));
subplot(221);
image(L');
subplot(222);
image(Lvyh');
| а) исходное изображение |  б) изображение а, обработанное глобальным методом нечеткого маскирования при к=1,1 |
 в) изображение а, обработанное глобальным методом нечеткого маскирования при к=1,5 |  г) изображение а, обработанное глобальным методом нечеткого маскирования при к=2 |
Рис. 2. Скользящая реализация метода нечеткого маскирования.
Обзор методов цифровой обработки изображений: Методы растяжения
Изображения, которые формируются во время различных исследований, часто не используют весь диапазон возможных градаций яркостей. Это предопределяет их низкую информативность. Контрастность изображения, яркости элементов которого расположены в узком промежутке возможных значений, низкая. Один из методов повышения качества таких изображений состоит в нелинейном преобразовании значений видеосигнала, в частности, в расширении области используемых значений градаций яркости на максимально возможный диапазон. Часто в основе таких преобразований лежит линейное растяжение или гамма-коррекция [1, 2]. Благодаря простой программной реализации и относительно высокому быстродействию, этот метод получил широкое применение [3, 4]. Преобразование, реализующее растяжение (см. рис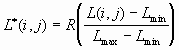. 1):
, (1)
где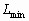 
, 
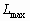- соответственно минимальная и максимальная яркости элементов изображения;
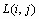- элемент изображения с координатами (i,j); R - максимальное значение яркости элементов изображения.
Выражение (1) осуществляет одинаковое растяжение для элементов разной яркости. Чтобы обеспечить нелинейное растяжение [3], используют модификацию выражения (1)
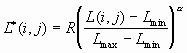, (2)
где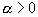 
.
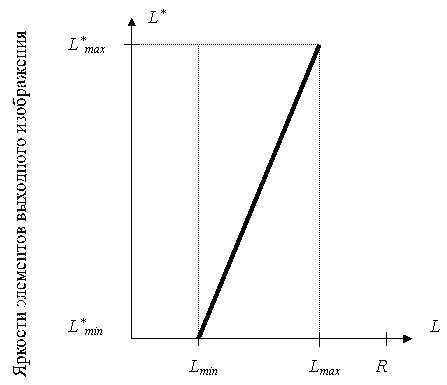
Яркости элементов исходного изображения
Рис. 1. Линейное растяжение яркостей элементов изображения
Методы линейного растяжения и гамма-коррекции являются базовыми при построении табличных (lookup table) методов [5]. Они имеют ряд недостатков, среди которых слабая адаптация к характеристикам конкретного изображения, поскольку в качестве характеристик изображения они используют лишь минимальное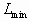 
и максимальное 
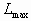значения яркостей его элементов. Вместе с тем никак не учитываются локальные особенности изображения и структура распределения яркостей элементов. С другой стороны, по закону формирования уровня адаптации зрительный механизм человека приспосабливается к определенному уровню яркости объекта [6]. В нашем случае этот уровень яркости отвечает усредненной яркости 
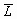всех элементов изображения
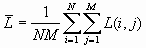, (3)
где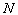 
, 
( 
, 
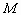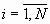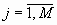) - размеры изображения 
.
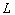Методы линейного растяжения и гамма-коррекции имеют еще один существенный недостаток, который состоит в том, что если яркости элементов изображения занимают максимально допустимый диапазон, а яркости элементов важных деталей – узкий промежуток, то улучшить контраст таких объектов этими методами достаточно тяжело. Использование других методов, которые решили бы эту задачу, связано с увеличением вычислительной сложности.
Итак, если динамический диапазон яркостей элементов изображения в целом приемлем, но значения градаций информативно важных объектов не распределены равномерно во всем промежутке, тогда методы растяжения не дают эффективного усиления контрастности. В качестве решения этой проблемы предложен метод кусочного растяжения с фиксацией узловой точки. Этот метод является обобщением известных методов растяжения и имеет более широкие функциональные возможности относительно улучшения разных классов изображений. Это касается, в первую очередь, изображений, динамический диапазон яркостей которых в общем приемлемый, а диапазон яркостей информативной части - узкий. В целом предложенный подход к преобразованию изображений позволяет существенно повысить эффективность их обработки простыми алгоритмическими средствами. Он служит основой построения быстрых методов повышения контраста изображений.
Экспериментальные исследования предложенного метода показали его преимущества в сравнении с известными методами того же класса.
Список литературы