Глава 2. Логические основы цифровой схемотехники

И так, что же из себя представляют логические ноль(ложь) и единица(истина) на схеме? Это некоторый уровень напряжения, например, для КМОП логики 0 – что-то в районе 0 В, 1 – напряжение питания.

Есть два основных класса цифровых устройств – комбинационные схемы и цифровые автоматы. Для первых, в каждый момент времени, значения выходных сигналов целиком определяются значением входных. Для вторых поправку вносит предыдущее состояние системы (автомат запоминает своё предшествующее состояние, и оно также рассматривается как входной параметр).

Комбинационная схема может быть задана таблицей, перечисляющей значения выходных параметров на полном множестве входных (таблица истинности) либо булевой функцией.

Булевой, или переключательной, функцией называется функция, принимающая значения из множества логических сигналов (0 и 1), аргументы которой также принадлежат данному множеству. Пусть имеется n переменных, каждая из которых может принимать значения 0 или 1, тогда общее количество комбинаций значений этих переменных равно 2ⁿ, а количество различных функций от n переменных ₂2ⁿ. Таким образом, для одной переменной Х существует 4 булевых функции (Х, не Х, константы 0, 1), для двух переменных – 16 возможных функций. Задавать булевы функции можно трёмя способами:

1) Табличный – перечисляются все возможные значения переменных и соответствующие им значения функции (таблица истинности)

X1	X2	X3	F(x1,x2,x3)

Рис. 3

2)
Графический – рисуется многомерный куб (от одной переменной – отрезок, от двух – квадрат, от трёх – куб и тд.), на данном кубе отмечаются вершины, где функция равняется 1.

Рис. 4

3) Аналитический – формулой. .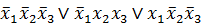

Хочу заметить, что во всех трёх примерах задана была одна и та же функция. Кстати, если несколько функций представлены одной и той же таблицей истинности, то они равны (это утверждение верно и для других способов задания функции). Переменные, от которых не зависит значение функции, называются фиктивными. Функция также может быть задана высказыванием, что, по сути, есть прочтение формулы.

Рис. 5

Рис. 6

Рис. 7

На рис. 5 даны таблицы истинности булевых функций от двух переменных, на рис. 6 – условные схемотехнические обозначения наиболее популярных функций, рис. 7 – названия булевых функций от двух переменных и эквивалентные обозначения.

Основы синтеза циф­ровых логических устройств

Рис. 8

На рис. 8 представлены основные аксиомы и теоремы булевой алгебры. Применяя эти тождества можно переходить от одного аналитического представления высказывания к другому (упрощая формулу, напр.), не стоит игнорировать простой и действенный способ проверки правильности своих манипуляций с формулой – использование таблицы истинности.