Графические формы решения многокритериальной задачи

Обычное графическое представление, например, в форме диаграмм, позволяет сравнивать по одному единственному критерию. Охватить несколько величин одновременно крайне затруднительно, а при большом их числе практически невозможно. Поскольку при принятии проектного решения приходится часто прибегать к нескольким критериям, отмеченный недостаток весьма существен.

Одним из многокритериальных способов выбора проектного решения является метод «паука». Название данного метода может показаться на первый взгляд несерьезным. Но поскольку итоговое графическое представление напоминает паутину (рис.26), то и смысл названия становится понятен.

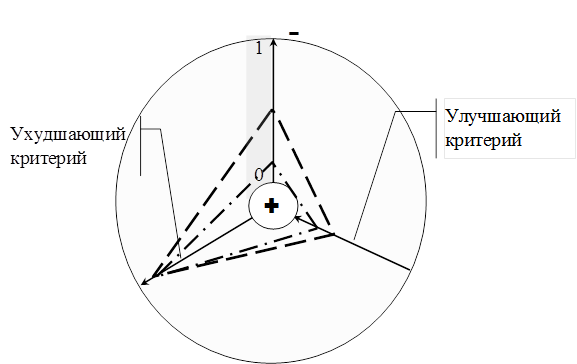
Рис. 1. Построение полярной системы координат
при графическом решении задачи методом «паука».

Метод «паука» не только требует графического представления полученных чисел, но использует для оценки само графическое изображение. Смысл и значение графических методов при поиске проектного решения заключается не столько собственно в методике, сколько в наглядности, придающей столь важную обозримость. Рассматриваемое с этих позиций графическое представление, разумеется, служит лишь вспомогательным средством, а не самостоятельным методом. Однако не стоит недооценивать эту функцию. Человек – не вычислительная машина: для него числа представляют собой лишь одну сторону дела, а более действенным оказывается наглядный зрительный образ. Полезно всегда помнить, что 80-90 % всей информации, которую мы воспринимаем из окружающего мира, поступает к нам через зрительный канал. Поэтому стоит чаще применять графическое представление при поиске проектного решения.

Отличительной чертой метода «паука» является то обстоятельство, что построения осуществляются не в декартовых, прямоугольных координатах, а в полярных. При этом центральная часть отражает лучшие решения, а периферия – худшие. Оси, на которые наносятся социальные показатели различных вариантов проектного решения, направлены от центра окружности к периферии, в том случае, если рост критерия ухудшает ситуацию, в противном случае – направление оси социального показателя от периферии к центру.

Для сравнения вариантов между собой осуществляется процедура нормирования, суть которой заключение всех социальных показателей в диапазон от 0 до 1. Это достигается деления исходных данных на максимально возможное значение этого показателя (P_max), которое лежит в диапазоне:

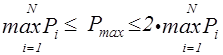, (7.9)

где P_i- значение социального показателя для i-того варианта, N – количество сравниваемых вариантов.

Следующим шагом нормированные показатели наносят на соответствующие оси. Выбор проектного решения осуществляют путем визуального сравнения полученных геометрических фигур между собой. При этом фигура с меньшей площадью отвечает лучшему варианту проектного решения.

Задание 2.Определить с помощью графического метода решения многокритериальной задачи (метода паука), какой их двух вариантов предполагаемого трудоустройства является более предпочтительным при равнозначности всех критериев и при 4‑кратной значимости критерия «заработная плата».

Варианты трудоустройства	Зар.плата, руб.	Время в пути, мин.	Условия труда, балл	Раб. день, ч.	Карьера, балл
			4,5	7,5	4,5
			3,5

Решение

1. Определим с помощью графического метода решения многокритериальной задачи предпочтительный вариант предлагаемого рабочего места при равнозначности всех критериев. Введем вспомогательные данные и коэффициенты значимости:

Максимальное значение			5,0
Коэф-т значимости	1,00	1,00	1,00	1,00	1,00
Вариант 1	0,30	0,96	0,23	0,84	0,23
Вариант 2	0,75	0,81	0,18	0,81	0,15

Осуществим нормирование данных и построим график (рис 27).

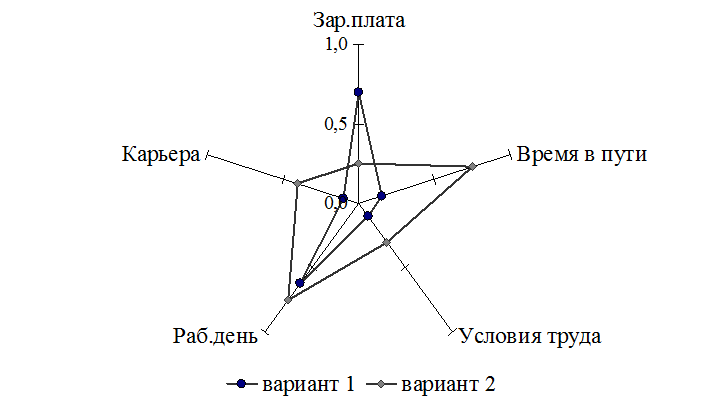
Рис. 27. Графическое решение многокритериальной задачи выбора рабочего места при равнозначности критериев

Таким образом, при равнозначности критериев более предпочтительным оказывается 1 вариант трудоустройства.

2. Определим с помощью графического метода решения многокритериальной задачи предпочтительный вариант предлагаемого рабочего места при4‑кратной значимости критерия «заработная плата». Введем вспомогательные данные и коэффициенты значимости, отражающие условие задачи:

Максимальное значение			5,0
Коэф-т значимости	1,00	0,25	0,25	0,25	0,25
Вариант 1	0,30	0,96	0,23	0,84	0,23
Вариант 2	0,75	0,81	0,18	0,81	0,15

Осуществим нормирование данных и построим график (рис. 28).

Рис. 28. Графическое решение многокритериальной задачи выбора рабочего места при4‑кратной значимости критерия «заработная плата»

Таким образом, при4‑кратной значимости критерия «заработная плата» более предпочтительным оказывается 2 вариант трудоустройства, с более высокой заработной платой.