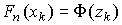Проверка нормальности распределения результатов наблюдений
В предыдущих разделах было показано, что результаты наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными.
При большом числе результатов наблюдений (n>40) данная задача решается в следующем порядке.
Весь диапазон полученных результатов наблюдений Xmax ... Xmin разделяют на r интервалов шириной 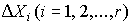 и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы.
и подсчитывают частоты mi, равные числу результатов, лежащих в каждом i-м интервале, т. е. меньших или равных его правой и больших левой границы.
Отношения
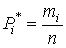 | (50) |
где n - общее число наблюдений, называются частостями и представляют собой статистические оценки вероятностей попадания результата наблюдений в i-й интервал. Распределение частот по интервалам образует статистическое распределение результатов наблюдений.
Если теперь разделить частость на длину интервала, то получим величины
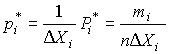 | (51) |
являющиеся оценками средней плотности распределения в интервале 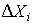 .
.
Отложим вдоль оси результатов наблюдений (рис.11) интервалы 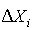 в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной
в порядке возрастания индекса i и на каждом интервале построим прямоугольник с высотой, равной 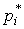 . Полученный график называется гистограммой статистического распределения.
. Полученный график называется гистограммой статистического распределения.

Площадь суммы всех прямоугольников равна единице:
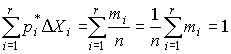
При увеличении числа наблюдений число интервалов можно увеличить. Сами интервалы уменьшаются, и гистограмма все больше приближается к плавной кривой, ограничивающей единичную площадь, - к графику плотности распределения результатов наблюдений.
При построении гистограмм рекомендуется пользоваться следующими правилами:
1. Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям табл.6.
| Таблица 6
|
2. Длины интервалов удобнее выбирать одинаковыми. Однако если распределение крайне неравномерно, то в области максимальной концентрации результатов наблюдений следует выбирать более узкие интервалы.
3. Масштабы по осям гистограммы должны быть такими, чтобы отношение ее высоты к основанию составляло примерно 5:8.
Пример. Было выполнено 100 измерений среднего диаметра резьбового калибра. Результаты наблюдений лежат в диапазоне 8.911 - 8.927 мм, т. е. зона распределения результатов составляет 0.016 мм. Весь диапазон удобно разделить на восемь равных интервалов через 0.002 мм. В табл.7 приведены частоты mi, частости 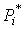 и плотности
и плотности 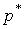 статистического распределения.
статистического распределения.
Таблица 7
|
После построения гистограммы надо подобрать теоретическую плавную кривую распределения, которая, выражая все существеные черты статистического распределения, сглаживала бы все случайности, связанные с недостаточным объемом экспериментальных данных. Принципиальный вид теоретической кривой выбирают заранее, проанализировав метод измерения, или хотя бы по внешнему виду гистограммы. Тогда определение аналитического вида кривой распределения сводится к выбору таких значений его параметров, при которых достигается наибольшее соответствие между теоретическим и статистическим распределением. Одним из методов решения этой задачи является метод моментов. При его использовании параметрам теоретического распределения придают такие значения, при которых несколько важнейших моментов совпадают с их статистическими оценками. Так, если статистическое распределение, определяемое гистограммой, приведенной на рис.11, мы хотим описать кривой нормального распределения, то естественно потребовать, чтобы математическое ожидание и дисперсия последнего совпадали со средним арифметическим и оценкой дисперсий, вычисленным по опытным данным. В предыдущем примере  мм,
мм, 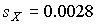 мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
мм и уравнение кривой нормального распределения, лучше всего согласующегося со статистическим распределением, должно иметь вид:
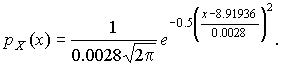
Далее законно возникает вопрос, объясняются ли расхождения между гистограммой и подобранным теоретическим распределением только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они вызваны тем, что результаты наблюдений в действительности распределены иначе?
Для ответа на этот вопрос используют методы проверки статистических гипотез. Идея их применения заключается в следующем. На основании гистограммы, полученной при обработке опытных данных, строится гипотеза, состоящая в том, что результаты наблюдений подчиняются распределению  с плотностью
с плотностью  .
.
Для того чтобы принять или опровергнуть эту гипотезу, выбирается некоторая величина U, представляющая собой меру расхождения теоретического и статистического распределений. В качестве меры расхождения можно принять сумму квадратов разностей частостей и теоретических вероятностей попадания результатов наблюдений в каждый интервал, взятых с некоторыми коэффициентами:
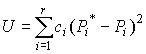 , , | (52) |
где  – коэффициенты, называемые весами разрядов;
– коэффициенты, называемые весами разрядов; 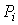 – теоретические вероятности, определяемые как
– теоретические вероятности, определяемые как
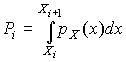 , , | (53) |
Здесь 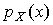 – предполагаемая плотность распределения.
– предполагаемая плотность распределения.
Мера расхождения U является случайной величиной и, независимо от исходного распределения подчиняется 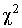 -распределению с k степенями свободы – см. формулу (44). Если значения всех частот
-распределению с k степенями свободы – см. формулу (44). Если значения всех частот 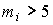 , число измерений стремится к бесконечности, а веса
, число измерений стремится к бесконечности, а веса 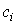 выбираются равными
выбираются равными 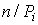 . Число степеней свободы распределения k = r - s, где
. Число степеней свободы распределения k = r - s, где 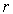 – число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частости
– число разрядов гистограммы статистического распределения, а s – число независимых связей, наложенных на частости 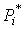 .
.
Если проверяется гипотеза о нормальности распределения, то к числу этих связей относится равенство среднего арифметического математическому ожиданию, а точечной оценки дисперсии - дисперсии предполагаемого нормального распределения. Кроме того, всегда требуется, чтобы сумма частостей по всем интервалам была равна единице. Поэтому в данном случае s = 3.
По табл.П.6 можно при заданной доверительной вероятности 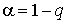 найти тот доверительный интервал
найти тот доверительный интервал 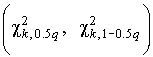 значений
значений  , в который мера расхождения может попасть по чисто случайным причинам.
, в который мера расхождения может попасть по чисто случайным причинам.
Если вычисленная по опытным данным мера расхождения окажется в указанном интервале, то гипотеза принимается. Это, конечно, не значит, что гипотеза верна. Можно лишь утверждать, что она правдоподобна, т.е. не противоречит опытным данным. Если же она выходит за границы доверительного интервала, то гипотеза отвергается как противоречащая опытным данным.
Поскольку проверка гипотезы основывается на опытных данных, то при принятии решения всегда возможны ошибки. Отвергая в действительности верную гипотезу, мы совершаем ошибку первого рода. Вероятность ошибки первого рода называется уровнем значимости и составляет 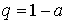 . Принимая в действительности неверную гипотезу, мы совершаем ошибку второго рода. Вычислить ее вероятность, вообще говоря, невозможно, поскольку для этого нужно рассмотреть все прочие возможные гипотезы, являющиеся альтернативой обсуждаемой гипотезы. Можно лишь утверждать, что при уменьшении ошибки первого рода ошибка второго рода увеличивается, поэтому не имеет смысла брать слишком высокие значения доверительных вероятностей.
. Принимая в действительности неверную гипотезу, мы совершаем ошибку второго рода. Вычислить ее вероятность, вообще говоря, невозможно, поскольку для этого нужно рассмотреть все прочие возможные гипотезы, являющиеся альтернативой обсуждаемой гипотезы. Можно лишь утверждать, что при уменьшении ошибки первого рода ошибка второго рода увеличивается, поэтому не имеет смысла брать слишком высокие значения доверительных вероятностей.
Описанная процедура проверки гипотезы о том, что данное статистическое распределение является распределением с плотностью 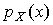 , называется критерием согласия
, называется критерием согласия 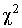 . Проверка нормальности распределения согласно критерию
. Проверка нормальности распределения согласно критерию 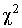 сводится к следующему.
сводится к следующему.
1. Данные наблюдений группируют по интервалам, как при построении гистограммы, и подсчитывают частоты 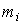 . Если в некоторые интервалы попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними. При этом число степеней свободы k, конечно, уменьшается.
. Если в некоторые интервалы попадает меньше пяти наблюдений, то такие интервалы объединяют с соседними. При этом число степеней свободы k, конечно, уменьшается.
2. Вычисляют среднее арифметическое 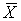 и точечную оценку среднеквадратического отклонения результата наблюдений
и точечную оценку среднеквадратического отклонения результата наблюдений 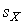 , которые принимают в качестве параметров теоретического нормального распределения с плотностью
, которые принимают в качестве параметров теоретического нормального распределения с плотностью 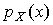 .
.
3. Для каждого интервала находят вероятности попадания в них результатов наблюдений либо по общей формуле (29), либо приближенно как произведение плотности теоретического распределения в середине интервала на его длину:
 . . | (54) |
4. Для каждого интервала вычисляют величины  и суммируют их по всем
и суммируют их по всем 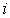 , в результате чего получают меру расхождения
, в результате чего получают меру расхождения  .
.
5. Определяют число степеней свободы 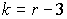 и, задаваясь уровнем значимости
и, задаваясь уровнем значимости  , находят по табл.П.6 приложения значения
, находят по табл.П.6 приложения значения  и
и  . Если
. Если  , то распределение результатов наблюдений считают нормальным.
, то распределение результатов наблюдений считают нормальным.
Критерий согласия  , построенный на предельном переходе при
, построенный на предельном переходе при 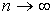 , рекомендуется применять, если общее число наблюдений больше сорока.
, рекомендуется применять, если общее число наблюдений больше сорока.
При малом числе наблюдений  нормальность распределения результатов наблюдений проверяется с помощью двух критериев.
нормальность распределения результатов наблюдений проверяется с помощью двух критериев.
Первый критерий основан на вычислении статистики
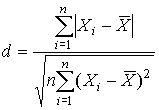 . . | (55) |
Гипотеза о нормальности распределения на основании первого критерия принимается, если при данном числе наблюдений и выбранном уровне значимости 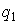 соблюдается условие
соблюдается условие
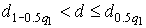 ,
,
где 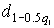 и
и 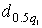 – квантили, выбираемые из табл.П.8.
– квантили, выбираемые из табл.П.8.
На основании второго критерия гипотеза о нормальности распределения принимается, если не более  разностей
разностей 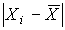 превосходят уровень
превосходят уровень  , где
, где 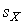 – оценка среднеквадратического отклонения результатов наблюдения,
– оценка среднеквадратического отклонения результатов наблюдения, 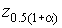 – квантиль интегральной функции нормированного нормального распределения, определяемый по данным табл.П.2 приложения при значении
– квантиль интегральной функции нормированного нормального распределения, определяемый по данным табл.П.2 приложения при значении

 .
.
Величина 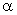 находится при заданном уровне значимости
находится при заданном уровне значимости  второго критерия по данным табл.П.9.
второго критерия по данным табл.П.9.
Распределение результатов наблюдения считается отличным от нормального, если оно не соответствует хотя бы одному из этих двух критериев. Уровень значимости составного критерия
 .
.
При малом числе наблюдений для оценки нормальности можно воспользоваться понятием статистической функции распределения результатов наблюдений. Для ее построения полученные в процессе эксперимента результаты группируют в так называемый вариационный ряд 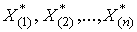 , члены которого располагаются в порядке их возрастания, так что всегда
, члены которого располагаются в порядке их возрастания, так что всегда  . Статистическую функцию распределения
. Статистическую функцию распределения 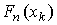 определяют по формуле
определяют по формуле
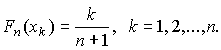 | (56) |
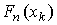 представляет собой ступенчатую линию, скачки которой соответствуют значениям членов вариационного ряда. Каждый скачок равен
представляет собой ступенчатую линию, скачки которой соответствуют значениям членов вариационного ряда. Каждый скачок равен 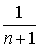 , если все
, если все 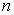 членов ряда различны. Если же для некоторого
членов ряда различны. Если же для некоторого 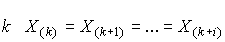 , то
, то 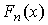 в точке
в точке 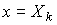 возрастает на
возрастает на  , где i – число равных между собой членов ряда.
, где i – число равных между собой членов ряда.
Если число наблюдений безгранично увеличивать, то статистическая функция распределения сходится по вероятности к истинной функции 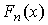 .
.
Для проверки нормальности распределения результатов наблюдений по табл.3 приложения находят значения 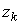 , соответствующие полученным значениям
, соответствующие полученным значениям 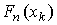 статистической функции распределения
статистической функции распределения  . Но переменная
. Но переменная 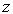 определяется через результаты наблюдений как
определяется через результаты наблюдений как
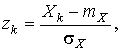
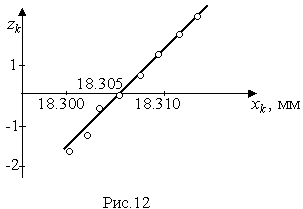
и если в координатах 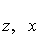 нанести точки
нанести точки 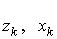 , то при нормальном распределении они должны расположиться вдоль одной прямой линии. Если же в результате такого построения получится некоторая кривая линия, то гипотезу о нормальности распределения придется отвергнуть как противоречащую опытным данным.
, то при нормальном распределении они должны расположиться вдоль одной прямой линии. Если же в результате такого построения получится некоторая кривая линия, то гипотезу о нормальности распределения придется отвергнуть как противоречащую опытным данным.
Пример. Даны результаты девятнадцати измерений длины детали (см. табл.3). Проверить нормальность распределения результатов наблюдений.
Вычисления по изложенной методике сведены в табл.8.
Таблица 8
|
На рис.12 представлена зависимость 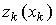 . Отдельные точки располагаются очень близко к прямой, поэтому распределение результатов наблюдений можно считать нормальным.
. Отдельные точки располагаются очень близко к прямой, поэтому распределение результатов наблюдений можно считать нормальным.

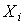 , мм
, мм 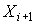 , мм
, мм  , мм
, мм