Расчет вероятности безотказной работы сложной частично резервированной системы

Цель работы:

1. Изучить методику расчета вероятности безотказной работы сложной частично резервированной системы, используя зависимости алгебры логики.

2. Научиться моделировать и рассчитывать безотказность работы частично резервированной системы с использованием алгебры логики.

Общие положения

При возможности расчленения сложной системы на элементы для расчета, исследования и управления надежностью используются структурные схемы. В структурных схемах элементы могут соединяться последовательно или параллельно.

При последовательном соединении:

Р₁ Р_i P_n

P_c(t)=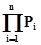

При параллельном соединении: Р₁

Р₂

Р_i

Р_m

Р_с(t)=1-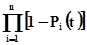

Для повышения надежности сложных систем применяют резервирование, то есть включение дополнительных элементов. При выходе из строя основного элемента, резервный продолжает работать (при нагруженном резервировании) или включается (при резервировании замещением).

Системы могут резервироваться полностью или частично. При этом в качестве элемента может рассматриваться самостоятельная (функционально) сложная система.

Рассмотрим, например, систему из трех элементов:

Р₁=0,99 Р₂=0,85 Р₃=0,995

1 2 3

Второй элемент резко снижает общую вероятность безотказной работы системы: Р_с(t)=0,99 0,85 0,995=0,837. Чтобы повысить надежность системы, нужно резервировать второй элемент. Имеет место нагруженное частичное резервирование по схеме:

1 3

Р₁=0,99 Р₃=0,995

Р₂=0,8

Р_с(t)=0,99[1-(1-0,85)²]0,995=0,99 0,9775 0,995=0,963

Для сложных структурных схем строятся логические схемы; схемы, основанные на алгебре логики.

В алгебре логики события обозначаются буквами латинского алфавита.

А – безотказность работы элемента. В графическом обозначении А

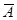(читается «не А») – отказ элемента. В графическом обозначении:

А

В – безотказность сложной системы.

или

Ú -дизъюнкция – логическое сложение, логическое обозначение «или» - графически « ».

и

Ù -конъюнкция - логическое умножение, логическое обозначение «и» - графически « ».

В графическом обозначении структурная схема, представленная выше, в алгебре логики выглядит следующим образом:

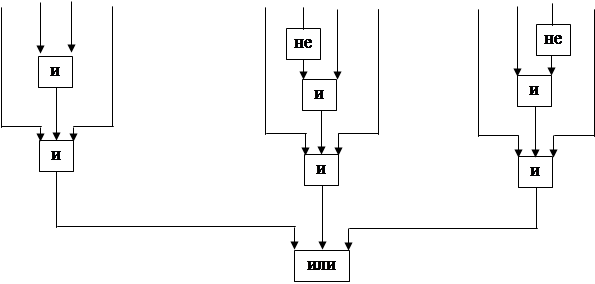А₁ А₂ 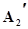А₃ А₁ А₂ 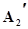А₃ А₁ А₂ 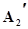А₃

В аналитическом виде модель безотказной работы системы имеет вид:

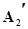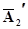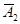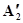В=(А₁ÙА₂Ù ÙА₃)Ú(А₁ÙА₂Ù ÙА₃)Ú(А₁Ù Ù ÙА₃)

или, переходя к вероятности:

Р_с(t)=Р₁·Р₂· 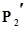·Р₃+Р₁·(1–Р₂)·Р₂·Р₃+Р₁·Р₂·(1– 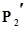)·Р₃=Р₁·Р₂·Р₃·(2–Р₂)

Порядок выполнения работы

1. Рассчитать в соответствии с заданным вариантом (таблица 1), вероятность безотказной работы сложной системы с частичным постоянным нагруженным резервированием.

1.1. Расчет выполнить с использованием логических схем и алгебры логики.

1.2. Расчет выполнить без использования алгебры логики и сравнить результат с расчетом по п. 1.1.

2. Построить логическую схему работы системы по заданной структурной схеме.

Таблица 1

Варианты заданий

№ варианта	Структурные схемы системы	Значение вероятностей безотказной работы элементов системы (Р)
Р1(t)	Р2(t)	Р3(t)	Р4(t)	Р5(t)
	Р2 Р4 Р1 Р3 Р5   Р’2 Р’4	0,985	0,9	0,99	0,905	0,995
	Р1 Р2 Р3 Р4 Р5   Р’1 Р’2	0,895	0,89	0,98	0,985	0,975
	Р3 Р5 Р1 Р2 Р4   Р’3 Р’5	0,99	0,985	0,91	0,995	0,905
	Р2 Р5 Р1 Р3 Р4   Р’2 Р’5	0,995	0,92	0,99	0,99	0,915
	Р4 Р5 Р1 Р2 Р3   Р’4 Р’5	0,975	0,98	0,985	0,885	0,89
	Р3 Р4 Р1 Р2 Р5   Р’3 Р’4	0,985	0,99	0,9	0,895	0,985
	Р1 Р5 Р2 Р3 Р4   Р’1 Р’5	0,9	0,995	0,985	0,99	0,91
	Р1 Р1 Р1 Р1 Р1   Р’1 Р’1	0,88	0,98	0,975	0,875	0,97
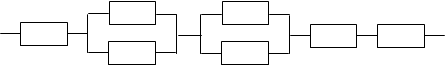	Р2 Р3 Р1 Р4 Р5   Р’2 Р’3	0,99	0,915	0,91	0,98	0,985
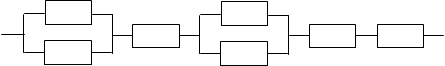	Р1 Р3 Р2 Р4 Р5   Р’1 Р’3	0,895	0,995	0,885	0,99	0,98

ПРАКТИЧЕСКАЯ РАБОТА № 5