Классификация измерений. Обоснованная классификация любых объектов представляет собой их условное группирование по заданным признакам
Обоснованная классификация любых объектов представляет собой их условное группирование по заданным признакам, осуществляемое с определенной целью. При различных целях одни и те же объекты могут быть классифицированы по-разному. Классификация не является самоцелью, она диктуется потребностями теории и практики. Целесообразность классификации измерений, т.е. подразделение этого понятие на группы, обуславливается удобством при разработке методик выполнения измерений и обработки результатов. Измерения могут быть классифицированы по ряду признаков.
Наибольшее распространение получила классификация по общим приемам получения результатов измерений. Согласно этому признаку, измерения делятся на прямые, косвенные, совместные и совокупные. Целью такого деления является удобство выделения методических погрешностей измерений, возникающих при определении результатов измерений.
Прямыми называются измерения, при которых искомое значение величины находят непосредственно по показаниям СИ. Например, масса, измеряемая при помощи весов, температура — термометром, напряжение — вольтметром.
Косвенные измерения — это измерения, при которых значение измеряемой величины находят на основании известкой зависимости между ней и величинами, подвергаемыми прямым измерениям, которые проводились в одинаковых условиях. Такие измерения имеют весьма важное значение для метрологической практики. На их основе, например, устанавливают значения, приписываемые эталонам единиц производных ФВ, исходя из значений единиц основных величин, воспроизводимых первичными эталонами. Широко применяются и менее точные косвенные измерения.
В общем случае зависимость, связывающую измеряемую величину Y и величины X1, Х2, ..., Хп, подвергаемые прямым измерениям, можно представить в виде
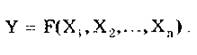 (2.3)
(2.3)
Например, измерение плотности р = m/V по результатам прямых измерений массы m и объема V; измерение активного сопротивления R=U/I по результатам прямых измерений напряжения U и тока I.
По виду функциональной зависимости F различают косвенные измерения:
• с линейной зависимостью
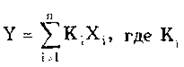
—постоянный коэффициент 1-го аргумента;
• с нелинейной зависимостью
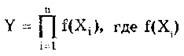
— некоторые функции;
• измерения с зависимостями смешанного типа
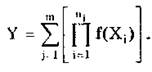
Вид связи между Y и Xi определяет методику расчета погрешностей косвенных измерений.
В современных микропроцессорных измерительных приборах очень часто вычисления искомой измеряемой величины производятся "внутри" прибора. В этом случае результат измерения определяется способом, характерным для прямых измерений, и нет необходимости и возможности отдельного учета методической погрешности расчета. Она входит в погрешность измерительного прибора. Измерения, проводимые такого рода средствами измерений, относятся к прямым. К косвенным относятся только такие измерения, при которых расчет осуществляется вручную или автоматически, но после получения результатов прямых измерений. При этом может быть учтена отдельно погрешность расчета. Характерный пример такого случая — измерительные системы, для которых нормированы метрологические характеристики их компонентов по отдельности. Суммарная погрешность измерений рассчитывается по нормированным метрологическим характеристикам всех компонентов системы.
Совокупными называются проводимые одновременно измерения нескольких одноименных величин, при которых их искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин. Совместными называются проводимые одновременно измерения двух или нескольких неодноименных величин для установления зависимости между ними. Как видно из приведенных определений, эти два вида измерений весьма близки друг к другу. В обоих случаях искомые значения находятся в результате решения системы уравнений, коэффициенты в которых получены путем прямых измерений. Отличие состоит в том, что при совместных измерениях одновременно определяются несколько одноименных величин, а при совокупных — разноименных.
Косвенные, совместные и совокупные измерения объединяются одним принципиально важным общим свойством: их результаты определяются расчетом по известным функциональным зависимостям между измеряемыми величинами и величинами, подвергаемыми прямым измерениям. Различие между этими видами измерений заключается только в виде функциональной зависимости, используемой при расчетах. При косвенных измерениях она выражается одним уравнением в явном виде (2.3), при совместных и совокупных — системой неявных уравнений. Поэтому уже неоднократно высказывались мнения [7] о сокращении "приведенной выше классификации. Все измерения делят на прямые и косвенные, которые в свою очередь подразделяются на несколько групп, различающихся между собой видом уравнений, представляющих функциональные зависимости между измеряемыми величинами и величинами, подвергаемыми прямым измерениям.
По характеристике точности измерения делятся на равноточные и неравноточные.
Равноточными называются измерения какой-либо ФВ, выполненные одинаковыми по точности СИ и в одних и тех же условиях. Соответственно неравноточными называются измерения ФВ, выполненные различными по точности СИ и (или) в разных условиях. Методика обработки результатов равноточных и неравноточных измерений различна.
В зависимости от числа измерений, проводимых во время эксперимента, различают одно- и многократные измерения. Однократными называются измерения, выполненные один раз, к многократными относятся измерения одного и того же размера ФВ, следующие друг за другом. Известно, что при числе отдельных измерений более четырех их результаты могут быть обработаны в соответствии с требованиями математической статистики. Это означает, что при четырех и более измерениях, входящих в ряд, измерения можно считать многократными. Их проводят с целью уменьшения случайной составляющей погрешности.
По отношению к изменению измеряемой величины измерения делятся на статические и динамические. Целью данной классификации является возможность принятия решения о том, нужно ли при конкретных измерениях учитывать скорость изменения измеряемой величины или нет. Погрешности, вызываемые влиянием скоростей изменения измеряемой величины, называются динамическими.
К статическим относятся измерения ФВ, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Динамические измерения — это измерения изменяющейся по размеру ФВ. Признаком, по которому измерение относят к статическому или динамическому, является динамическая погрешность при данной скорости или частоте изменения измеряемой величины и заданных динамических свойствах СИ. Предположим, что она пренебрежимо мала (для решаемой измерительной задачи). В этом случае измерение можно считать статическим. При невыполнении указанных требований оно является динамическим.
В зависимости от метрологического назначения измерения делятся на технические и метрологические. Технические измерения проводятся рабочими СИ. Метрологические измерения выполняются при помощи эталонов с целью воспроизведения единиц ФВ для передачи их размера рабочим СИ.
При метрологических измерениях в обязательном порядке учитываются погрешности, а при технических — принимается наперед заданная погрешность, достаточная для решения данной практической задачи. Поэтому при технических измерениях нет необходимости определять и анализировать погрешности получаемых результатов. Технические измерения являются наиболее массовым видом.
В зависимости от выражения результатов измерений последние подразделяются на абсолютные и относительные. Абсолютное измерение основано на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Понятие "абсолютное измерение" применяется как противоположное понятию "относительное измерение" и рассматривается как определение величины в ее единицах.
Относительное измерение — это измерение отношения определяемой величины к одноименной. Например: измерение активности радионуклида в источнике по отношению к активности радионуклида в однотипном источнике, аттестованном в качестве образцовой меры активности. Относительные измерения при прочих равных условиях могут быть выполнены более точно, чем абсолютные, поскольку в суммарную погрешность не входит погрешность меры величины.
