Метод Хао Вонга доказательства общезначимости(противоречивости)формул ИВ. Пример.

Этот метод представляет процедуру для обоснования или опровержения формул A₁, …, A_n |— B. Порядок действий можно представить в виде следующей схемы.

1. Если какая-либо формула имеет вид 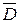, то перенести эту формулу на другую сторону относительно знака “|—“, опустив отрицание, например, строка

A V B, 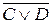, 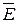|— S,

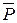
переходит в строку

A V B, P |— S, C V D, E.

2. Если слева от знака “|—“ в какой–то формуле главной связкой является “&”, а справа – “V”, то заменить эти связки запятыми. Например:

A & B, C & |—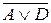

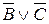
переходит в

A, B, C, |— , .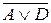

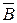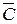3. Если главной связкой в формуле слева от “|—“ является “V”, а справа – “&”, то образовать два новых выражения, каждое из которых содержит одну из двух подформул, заменяющих исходную формулу. Например, из A, 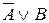|— B получаются строки: 1) A, 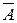|— B; 2) A, B |— B. Чтобы обосновать выводимость исходной формулы, требуется доказать все полученные таким образом строки.

4. Если одна и та же формула находится с обеих сторон от знака “|—“, то строка доказана.

5. Если в строке не остаётся ни одной связки и если ни одна переменная не присутствует с обеих сторон от знака “|—“, то строка недоказуема. Если же все переменные в левой части от “|—“ истинны, а в правой части ложны, то исходное утверждение опровергается.

Пример 2. Доказать ( A → B ) & ( B → C ) & A |— C.

Доказательство

A → B = 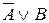, B → C = 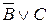. Тогда исходная формула принимает вид: 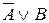, , 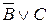A |— C.

1) 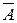, , 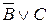A |— C

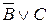, A |— C, A – строка доказана.

2) B, 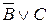, A |— C

а) B, 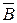, A |— C

B, A |— C, B – строка доказана.

б) B, C, A |— C – строка доказана.

7.Основные понятия и определения логики предикатов.Определение формулы логики предикатов.

Определение. Одноместным предикатом P(x) называется всякая функция одного переменного, в которой аргумент x приобретает значения из некоторого множества M, а функция P при этом принимает два логических значения – “истина” или “ложь” (обозначения: {и, л}, {0, 1}).

Множество M, на котором задан предикат, называется областью определения предиката.

Множество 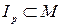, на котором предикат принимает только истинные значения, называется областью истинности предиката P(x).

Предикат P(x) называется тождественно истинным (тождественно ложным) на множестве M, если I_p = M (I_p = Ø).

Определение. n–местным предикатом называется функция P(x₁, x₂, …, x_n) от n переменных, принимающих значения из некоторых предметных областей, так что 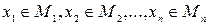, а функция P принимает два логических значения – “истина” или “ложь”. Таким образом, предикат P(x₁, x₂, …, x_n) является функцией типа P: 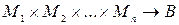, где множества M₁, M₂, …, M_n называются областями определения предиката; x₁, x₂, …, x_n – предметными переменными предиката; B – двоичное (бинарное) множество: B = {и, л} или {1, 0}.

Говорят, что предикат P(x) является следствием предиката Q(x) (Q(x)) → P(x)), если 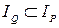; и предикаты P(x) и Q(x) равносильны (Q(x)) ↔ P(x)), если .

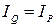Определение. Пусть P(x) – предикат, определённый на M, то есть x Є M. Высказывание “для всех x из M P(x) истинно” обозначается 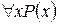; знак 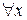называется квантором всеобщности. Высказывание “существует такой x из M, что P(x) истинно” обозначается 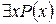; знак 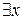называется квантором существования.

Переход от P(x) к 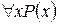или 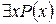называется связыванием переменной x, или навешиванием квантора на переменную x, или квантификацией переменной x.

Переменная, на которую навешен квантор, называется связанной, а несвязанная переменная называется свободной.

В логике предикатов используются следующие символы:

1. Символы p, q, r, … - переменные высказывания, принимающие два значения: {и, л}, {1, 0}.

2. Предметные переменные – x, y, z, …, которые пробегают значения из некоторого множества M: x⁰, y⁰, z⁰, … - предметные константы, то есть значения предметных переменных.

3. P(•), F(•) – одноместные предикатные переменные; Q(•,•, …, •), R(•,•, …, •) – n-местные предикатные переменные. P⁰(•), Q⁰(•,•, …, •) – символы постоянных предикатов.

4. Символы логических операций: &, V, →, ¯.

5. Символы кванторных операций: , .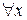

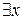6. Вспомогательные символы: скобки, запятые.

7. Равносильные преобразования формул логики предикатов. Предварённая нормальная форма (ПНФ) в логике предикатов.

Определение. Две формулы логики предикатов A и B называются равносильными на области M, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесённых к области M.

Определение. Две формулы логики предикатов A и B называются равносильными, если они равносильны на всякой области.

Пусть A(x) и B(x) – переменные предикаты, а C – переменное высказывание. Имеют место следующие равносильности логики предикатов:

1. .

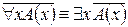2. .

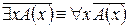3. .

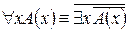4. .

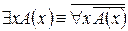5. .

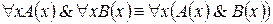6. .

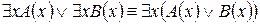7. .

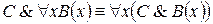8. .

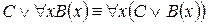9. .

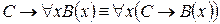10. .

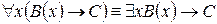11. .

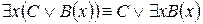12. .

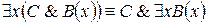13. .

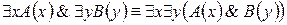14. .

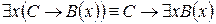15. .

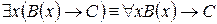Определение. Говорят, что формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам.

Определение. Предварённой нормальной формой (п.н.ф.) формулы логики предикатов называется её нормальная форма, имеющая вид:

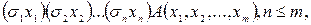
где 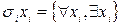, а формула A кванторов не содержит.