Переход от автомата Мили к эквивалентному автомату Мура и наоборот
Пусть конечный автомат Мили имеет функцию переходов fa(a, x) и функцию выходов fb(a, x). Найдем функцию переходов fb(b, x) и выходов jb(b) автомата Мура, эквивалентного заданному автомату Мили. Поставим в соответствие каждой паре, включающей состояние аiи входной сигнал xjавтомата Мили, состояние bijавтомата Мура. Кроме того, в множестве состояний автомата Мура включим начальное состояние а0автомата Мили, обозначив его через b0. Для автомата Мили, заданного таблицами переходов и выходов на рис. 29, такое соответствие можно представить в виде таблицы кодирования (см. рис. 34). Таблицу переходов эквивалентного автомата Мура строим в такой последовательности.
1. Выписать из таблицы кодирования состояния автомата Мили и соответствующие каждому состоянию множества состояний автомата Мура:
 | a0={b0, b02, b12, b22, b32}, a1=b01, a2=b11, a3={b21, b31}. 2. Если состояние bij входит в множество, соответствующее состоянию ар, то в колонку таблицы переходов автомата Мура для состояния bij следует записать состояния, находящиеся в колонке для ар (таблицы кодирования). Например, колонки таблицы переходов автомата Мура с состояниями b0, b02, |
b12, b22, b32 совпадают с колонкой для a0 таблицы кодирования, колонка b01 – с колонкой для a1и т.д.
Чтобы отметить выходными сигналами состояния достаточно наложить таблицу выходов автомата Мили на таблицу кодирования состояний автомата Мура и каждое состояние отметить тем выходным сигналом, с которым оно совпадает. Таблица переходов автомата Мура приведена на рис. 35.
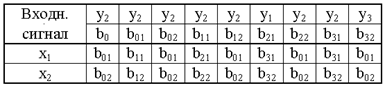
Рис. 35. Таблица переходов автомата Мура
Обратная задача перехода от автомата Мура к эквивалентному автомату Мили решается следующим образом. Таблицы переходов автомата Мили и эквивалентного ему автомата Мура совпадают. Таблица выходов автомата Мили составляется так, что в каждую клетку таблицы записывается выходной сигнал, которым отмечено состояние, расположенное в данной клетке. При этом граф автомата Мили отличается от графа автомата Мура только тем, что выходные сигналы из каждого узла переносятся на все ветви, которые входят в данный узел.
Эквивалентные автоматы, полученные по рассмотренным алгоритмам, могут иметь “лишние” внутренние состояния. Число состояний автомата может быть минимизировано.
Могут быть автоматы, на входы которых некоторые последовательности сигналов никогда не подаются. Такие последовательности называют запрещенными входными словами, а автоматы с запрещенными входными словами называют частичными автоматами. Граф частичного автомата имеет вершины, у которых количество выходящих ветвей меньше количества букв входного алфавита. При синтезе производят доопределение частичного автомата так, чтобы соответствующая ему схема содержала минимальное число элементов.
