КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же постоянной величины получаются результаты измерений

При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же постоянной величины получаются результаты измерений (наблюдений), как отличающиеся друг от друга, так и совпадающие. Такие расхождения в результатах измерений говорят о наличии в них случайных погрешностей. Каждая случайная погрешность возникает при одновременном воздействии многих источников. Каждый из этих источников сам по себе оказывает незаметное влияние на результат измерения, но суммарное воздействие всех источников может оказаться достаточно сильным. Случайные погрешности можно оценить методами математической статистики с привлечением теории вероятности при многократных измерениях одной и той же величины.

Для оценки точности результатов измерений, содержащих случайные погрешности, существует несколько способов. Наиболее распространена оценка точности в виде среднего квадратического отклонения результата наблюдений, под которым понимают параметр функции распределения результатов наблюдений, характеризующий их рассеивание и равный корню квадратному из дисперсии результата наблюдений с положительным знаком. Для нахождения среднего квадратического отклонения необходимо знать закон распределения случайной погрешности. В практике электрических измерений встречаются различные законы распределения. Если соблюдены условия возможности применения центральной предельной теоремы вероятностей, можно считать, что закон распределения суммарной случайной погрешности нормальный.

Составляющая погрешности измерения, остающаяся постоянно или закономерно изменяющаяся при повторных измерениях одной и той же величины, называется систематической погрешностью измерения (Δ_с).

Поведение систематической погрешности можно предсказать. Т.е. можно предсказать, когда она появится, какое будет ее значение. Пример систематической погрешности: стрелка прибора стоит не на нуле при нулевом значении величины. Во многих случаях систематическую погрешность можно исключить или уменьшить ее влияние, отрегулировав прибор до начала проведения измерений или внести поправку в запись результатов измерения, которая по значению равна величине систематической погрешности (поправка может быть со знаком «+» или «­»). Например, при нулевом значении величины стрелка показывает значение а (рис. 1). Значит, когда, при измерении ненулевого значения величины стрелка остановится на числе Х, то действительное значение величины будет равно Хд=Х-а.

Рис. 1 Пример систематической погрешности

В отличие от систематической погрешности случайную погрешность исключить нельзя, поскольку мы не знаем ее поведения: не можем предсказать, когда она появится и какое будет ее значение. Однако ее влияние может быть уменьшено, если применить специальные методы обработки результатов измерений, основанных на положениях теории вероятностей и математической статистики. Мы не можем избавиться от случайной погрешности, но при помощи математической статистики мы можем выяснить, в каком интервале лежат значения измеренной величины. Если мы измерим одну и ту же величину много раз, найдем ее математическое ожидание и СКО, то наиболее точно сможем определить интервал, в котором она находится с заданной вероятностью.

Нормальный закон (Гаусса) базируется на двух аксиомах:

- при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто;

- чаще всего встречаются меньшие погрешности, а большие погрешности встречаются тем реже, чем они больше.

Математически нормальное распределение случайных погрешностей может быть представлено формулой:

,

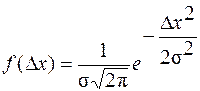где 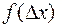- плотность вероятности случайной погрешности ;

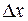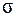- среднее квадратическое отклонение.

Согласно теории вероятностей среднее квадратическое отклонениеслучайной погрешности ряда измерений может быть приближенно выражено в виде:

.

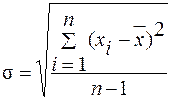Если 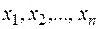- совокупность измеренных значений величины x, то за оценку результата измерения принимают среднее арифметическое значение:

.

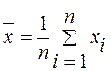В качестве оценки среднего квадратического отклонения результата измерения принимают:

.

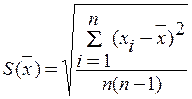При проведении измерений стремятся получить результат измерения с погрешностью, не превышающей допускаемое значение. Знание только среднего квадратического отклонения не позволяет найти максимальную погрешность, которая может встретиться при измерениях, что свидетельствует об ограниченных возможностях этой числовой характеристики.

Максимальные значения погрешности зависят не только от среднего квадратического отклонения, но и от вида закона распределения. Когда распределение погрешности теоретически неограниченно, например, при нормальном законе распределения, погрешность может быть любой по значению. В этом случае можно лишь говорить об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным интервалом, характеризующую его вероятность – доверительной вероятностью, а границы этого интервала – доверительными значениями погрешности (доверительными границами).

Доверительные границы 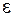(без учета знака) случайной составляющей погрешности результата измерения находят по формуле

,

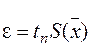где 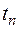- коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности .

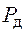Для определения доверительных границ погрешности результата измерения доверительную вероятность в соответствии с ГОСТ 8.207-76 принимают равной 0,95. В тех случаях, когда измерение нельзя повторить или результаты измерений имеют значение для здоровья людей, помимо границ, соответствующих 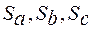указывают границы для доверительной вероятности 0,99 и выше.

Измерения в зависимости от способа обработки экспериментальных данных для нахождения результата относят к прямым, косвенным, совместным и совокупным.

Прямое измерение- это измерение, при котором искомое значение величины находят непосредственно из опытных данных в результате выполнения измерения.

Косвенное измерение – это измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергающимися прямым измерениям.

Совместное измерение – это одновременное изменение нескольких неодноимённых величин для нахождения зависимости между ними. При этом решают систему уравнений.

Совокупное измерение– это одновременное изменение нескольких одноимённых величин, при котором искомое значение величин находят решением системы уравнений, состоящее из результатов прямых измерений, различных сочетаний этих величин.

При косвенных измерениях результат 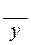находится по известной функциональной зависимости между измеряемой величиной y и величинами a, b, c, …, которые могут быть определены прямыми измерениями.

Погрешности косвенных измерений величины y зависят от погрешностей прямых измерений величин a, b, c.

Для оценки результатов косвенных измерений величины y будем считать, что систематические погрешности измерений величин a, b, c исключены, а случайные погрешности измерения этих величин не зависят друг от друга, т.е. не коррелированны.

Для вычисления среднего квадратического отклонения результата 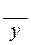измеряемой величины y используют средние квадратические отклонения, полученные при прямых измерениях величин a, b, c.

В общем виде при нелинейной зависимости между y и a, b, c отклонение результатов косвенного измерения 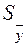определяется как

,

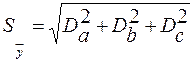где 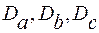- частные погрешности косвенного измерения, равные

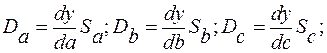
где 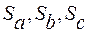- средние квадратические отклонения результатов прямых измерений величин a, b, c.

Погрешность результата косвенных измерений в доверительных границах при заданной доверительной вероятности 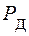определяется как

,

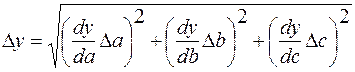где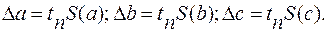

ЗАДАНИЕ

3.1. Изучить вероятностные методы обработки результатов прямых и косвенных измерений.

3.2. Произвести 10 измерений активного сопротивления резистора с помощью цифрового омметра.

3.3. Собрать схему для измерения активного сопротивления резистора порядка 100÷300 Ом на постоянном токе и произвести не менее 10 прямых измерений напряжения и однократное измерение тока.

3.4. Произвести обработку прямых измерений сопротивления, напряжения и тока. Найти результаты, показатели точности и достоверности результата измерения.

3.5. Произвести обработку косвенных измерений. Найти результата и показатели точности и достоверности результата измерения.

3.6. Сравнить результаты прямых и косвенных измерений сопротивления.