Облегченное резервирование замещением

При облегченном резерве запасной элемент до его включения в основной режим работает под неполной нагрузкой и поэтому тоже может отказать.

Вероятность безотказной работы системы, имеющей одно основное и k резервных устройств, рассчитывается по рекуррентной формуле

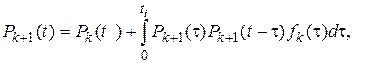(4.31)

где P_k(t) - вероятность безотказной работы системы, имеющей одно основное и k - 1 резервных устройств;

Р_k+1(τ) - вероятность безотказной работы (k+1)-гoре­зервного устройства до момента τ включения его в рабо­ту;

P_(k+1)(t - τ) — вероятность безотказной работы (k+1)-го резервного устройства в течение наработки (t - τ)от момента τ включения его в работу до момента t;

f_k(τ) — плотность распределения наработки до отказа системы, имеющей одно основное и k - 1 резервных уст­ройств.

В случае показательного распределения наработки до отказа

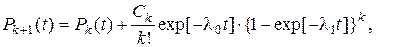(4.32) где 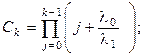λ₀ – интенсивность отказов работающего устройства, λ₁ интенсивность отказов резервного устройства, находящегося в облегченном резерве (λ₁ < λ₀ ).

Средняя наработка до отказа системы

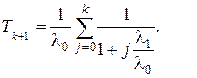(4.33)

Резервирование с учетом надежности переключателей

При общем нагруженном резервировании (рис. 4.2, в)вероятность безотказной работы системы

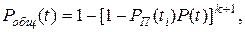(4.34)

где P(t) - вероятность безотказной работы основной или резервной системы в течение наработки (0, t),

P_П(t) - вероятность безотказной работы переключаю­щего устройства в течение наработки (0, t).

Прираздельном нагруженномрезервировании веро­ятность безотказной работы

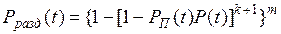. (4.35)

Скользящее резервирование

Логическая схема представлена на рис 2.4, д. В случае одного нена­груженного резервного и m работающих элементов система может находиться в течение наработки (0, t)в одном из двух несовместных работоспособных состояниях:

- все элементы основной системы работают безотказно;

- отказал один основной элемент из общего числа m+1 элементов, причем переключатель ра­ботоспособен.

Суммируя вероятности этих состояний, по­лучаем:

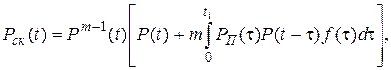(4.36)

где Р_П(τ) - вероятность безотказной работы переключа­теля до момента τ включения резервного элемента;

P(t-τ) - вероятность безотказной работы резервного элемента с момента τ его включения; f(τ) - плотность распределения наработки до отказа одного элемента основной системы;

P(t) - вероятность безотказной ра­боты одного элемента основной системы.

При показательном распределении наработки до отказа

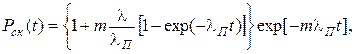(4.37)

где λ - интенсивность отказов работающего элемента;

λ_П - интенсивность отказов переключателя.

В случае двух резервных элементов необходимо рас­сматривать четыре несовместных состояния, при которых возможна безотказная работа системы.

____________

4.1. Александровская Л.Н. Современные методы безотказности сложных технических систем: учебник / Л.Н. Александровская, А.П. Афанасьев, А.А. Лисов. М.: Логос, 2003.

4.2. Теория надежности электронных систем в примерах и задачах / под ред. Г.В. Дружинина; Г.В. Дружинин, С.В. Степанов, В.Л. Шихматова, Г.А. Ярыгин. М.: Энергия, 1976.

4.3. Иыуду К.А. Надежность, контроль и диагностика вычислительных машин и систем / К.А. Иыуду. М.: Высшая школа, 1989.