Рассуждения на основе дедукции, индукции и аналогии

Различают следующие виды логических рассуждений:

1) рассуждение от сложного к простому или рассуждение на основе дедукции.

Другими словами дедукция - это получение частного правила на основе общего правила. Например, правила решений квадратных уравнений в общем случае выглядит так: Необходимо определить дискриминант и в зависимости от того, какое значение примет этот дискриминант (>0,=0,<0) делается вывод о том, что квадратное уравнение имеет 2 корня, один корень или не имеет ни одного, а частные правила для решения квадратного уравнения можно считать по теореме Виета. Она применима только для уравнений, у которых коэффициент при x2 равен единице.

2) Рассуждение от простого к сложному или рассуждение на основе индукции

Индукция - это когда на основе частных примеров синтезируются общие правила.
Например, метод математической индукции из школьного курса математики гласит, что если формула верна при n=1,2,…,k, то она будет верна и для n=k+1, то она верна для всех n.

3) Рассуждение на основе прошлого опыта или по аналогии
Аналогия - это скрытая (неявная) закономерность, которая присуще многим на первый взгляд внешним различающимся объектам.

Например, было у меня три собаки, одна из них прожила 8 лет, другая - 10 лет и можно сделать вывод, что собака живет от 8 до 15 лет; собаки преданные друзья.

37.Машина логического вывода, основные понятия.

Модель машины логического вывода (МЛВ) – программа обработки знаний. Подсистема ЛВ строит И/ИЛИ дерево целей на основе правил и фактов БД и целей. Для ускорения процедуры ЛВ используют механизмы упрощения – эвристические правила, чтобы ускорить процесс получения результата.

Исчисление – это совокупность правил оперирования с какими-либо символами. Исчисление высказываний – совокупность правил, используемых для определения истинности или ложности некоторой комбинации высказываний. Совокупность этих правил можно смоделировать на вычислительной машине, которая, таким образом, получает возможность рассуждать. Весьма общие рассуждения позволяют проводить набор правил.

Рассуждения – исчисление предикатов, в частности, метод резолюции, который применим и к исчислению высказываний [1].

Предикат – это функция от одного или нескольких аргументов с булевскими значениями "истина" и "ложь". Например, в языке логического программирования Пролог использован метод резолюций исчисления предикатов.

38.Логический вывод.

Логический вывод (ЛВ) – формальный метод доказательства в ЭС и задачах, решаемых в системах ИИ. Он имеет два аспекта: использование рассуждений для нахождения различных предположений, которые обусловлены имеющимися фактами и правилами, или изучение заключений, которые представляют интерес и могут быть (а могут и не быть) истинными. Первый метод носит название индуктивного (прямого, рассуждения ведутся от частного к общему) метода, второй – дедуктивного (обратного, рассуждения от общего к частному) метода. При помощи правил вывода получают новые результаты на основе известных. Но иногда, логика дает осечки. В качестве классического примера приводится случай с Протагором, который во времена Аристотеля обучал молодых людей искусству рассуждать, выступая на суде[]. Один из его учеников заметил, что платить деньги за обучение надо не после окончания школы, а после того, как он выиграет первый процесс, дабы убедиться, что наука пошла впрок. Протагор подал на него в суд. Юноша решил доказать, что он не должен платить своему учителю. В любом случае выиграет юноша процесс или нет, он должен платить за обучение, а это означает, что он проиграл.

40.Нечеткий вывод знаний. Немонотонность вывода.

Нечеткий вывод знаний

В реальном мире многие процессы имеют не детерминированную случайную природу. Поэтому человек рассуждает о таких явлениях не точно, а приближенно. Аналогично для вывода знаний в компьютерных интеллектуальных системах были разработаны методы нечеткой логики и соответственно теории нечетких выводов знаний. Например, студенты сдают экзамены. Один студент знает блестяще, другой - хорошо, третий - плохо, но эти оценки не точные, а приближенные. Поэтому часто на экзамене студент, знающий предмет блестяще получает оценку "хорошо", а студенты, которые знают предмет хорошо, получают иногда "отлично" или "удовлетворительно". Это говорит не только о нечеткости оценки знаний студентами, но и о нечеткости самого процесса оценивая знаний студента преподавателем на экзамене.

Не монотонность вывода

Не монотонность логического вывода означает, что вывод может никогда не закончится и не дать ответа. Другими словами есть не разрешимые проблемы в принципе, либо разрешимы, для некоторого конкретного метода.

Не разрешимые проблемы в принципе - это такие проблемы, которые нельзя решить ни одним из существующим методом, но также ни одним из методом, которые когда либо будет создан.

41.Логический вывод в условиях неполной информации.

Знания в реальной жизни требуют учета неопределенностей. Предложены различные варианты использования фрагментарной и ненадежной информации для получения оценки истины. Преимущества ЭС – быть точными в отношении неточностей. Точный вывод сделать относительно просто. Тип логического вывода, который имеет дело с неопределенностью, не является простым, точным и легким. Эксперты – люди, которые во все моменты времени прибегают к неточным и трудным выводам. Для учета неопределенности используют [2]:

- нечеткую логику,

- коэффициенты уверенности,

- вероятностный подход,

- подход с ценами свидетельств и др.

42.Нечеткая логика.

В нечеткой логике, предложенной Л. Заде, для указания частичной истины используется весь диапазон нецелочисленных значений булевой алгебры от 0 до 1.

Запись р(hight(X))=0.7 свидетельствует о том, что факт "X – высокий" в некотором смысле истинен на 0.7.

43.Коэффициенты уверенности.

Для измерения степени доверия к любому заключению, являющемуся результатом имеющихся свидетельств, можно использовать коэффициенты уверенности [].

Коэффициент уверенности – это разность между двумя мерами:

КУ[h:e]=МД[h:e]-МНД[h:e]

где: КУ[h:e] – уверенность в гипотезе h при наличии свидетельства e,

МД[h:e] – мера доверия h при заданном e,

МНД[h:e] – мера недоверия гипотезе h при свидетельстве e.

КУ изменяется от -1 до 1, принимая все промежуточные значения. МД и МНД изменяются в пределах от 0 до 1.

Возникает проблема со шкалированием субъективных суждений. Здесь необходимо прибегать к помощи экспертов.

44.Байесовский подход к построению логического вывода.

Р. Байес – английский священник, живший в 18 веке, много времени уделявший статистике. Правило Байеса позволяет оценивать гипотезу, если имеет место свидетельство, подтверждающее эту гипотезу (событие).

где: P(H) – априорная вероятность Н при отсутствии свидетельств,

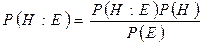P(H:E) – апостериорная вероятность H при наличии свидетельства Е,

P(E) – вероятность свидетельства.

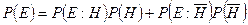Для вычисления P(E) можно воспользоваться выражением:

Формула применяется многократно при появлении новых свидетельств, при этом априорная вероятность каждый раз заменяется на апостериорную.

Эффективность работы МЛВ зависит от контекста правил, набора и расположения правил, а также выбранного формата представления знаний в БЗ.

45.Учет неметризуемых факторов.

У многих факторов нет выражения в каких-либо единицах. Относительная значимость таких факторов определяется интуитивно, при этом приходится сравнивать многие разнородные переменные, часть из которых вообще не имеет естественной шкалы для измерения. Между такими переменными нет арифметических операций, а возможно только ранжирование [].

Ранг – это показатель, характеризующий порядковое место оцениваемого объекта или явления в группе таких же объектов (явлений).

Ранжирование – процедура установления относительной значимости исследуемых объектов на основе их предпочтительности друг перед другом. Наиболее предпочтительному объекту присваивается первый ранг. Для установления ранга привлекаются независимые эксперты. В общем случае каждый эксперт при ранжировании должен расположить все объекты в порядке, который он считает наиболее рациональным, и приписать каждому числа натурального ряда: 1, 2, 3, и т.д. Точность и надежность ранжирования зависят от количества объектов. Так как ранг не дает ответ на вопрос, насколько один вариант лучше другого, метод ранжирования применяют в сочетании с методом непосредственной оценки. Для этого разрабатывают шкалу интервалов, каждой градации которой присваивается определенный вес. С точки зрения экспертов, величины интервалов должны быть равными. Эксперт помещает объекты в определенный оценочный интервал.

Надежность и достоверность решений принимаемых группой экспертов зависит от варианта процедуры организации опроса экспертов.

Один из вариантов опроса – метод Дельфи (в храме греческого города Дельфи находился знаменитый во всем античном мире оракул, предсказывающий будущее). Сущность метода Дельфи – эксперты остаются анонимными и не общаются друг с другом. Сначала ранжируются представленные варианты. Подсчитываются средние значения, медианы и квартили. Медиана – это середина упорядоченного ряда, а квартили –

середины отрезков, образованных слева и справа от медианы. За показатель группового мнения принимается медиана, а за характеристику согласования мнений экспертов – диапазон квартилей. Эксперты, оценки которых выходят

за диапазоны верхнего и нижнего квартилей, обосновывают свои суждения и сообщают свои мнения относительно правильности постановки вопроса. Их аргументы могут включать ряд дополнительный факторов, которые не учитывались другими специалистами. Эти аргументы доводятся до всех других специалистов. Процедура оценки повторяется таким образом многократно, Медиана оценок последнего тура принимается за обобщенное мнение.