Эксперименты с автоматами

1. Привести пример неприводимого автомата, у которого существует установочный эксперимент.

2. Для каких алфавитов справедлива теорема Мура об установочных экспериментах?

3. Какие бывают эксперименты?

4. Могут ли не совпадать автоматы, простые эксперименты которых совпадают?

Регулярные выражения и события.

1. Регулярность множества всех слов с квадратной длиной.

2. Лемма о накачке.

3. ­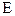 не регулярно. Может ли быть регулярно ?

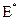4. Регулярно ли событие состоящее из слов вида , ?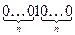

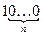5. Регулярно ли событие, полученное из регулярного выбрасыванием вторых (последних) букв?

6. Можно ли представить автоматом конечное множество слов?

7. Привести пример автомата, представляющего некоторое бесконечное множество слов.

8. Регулярность множества выходов автоматов.

9. Автомат, представляющий пустое событие.

10. Регулярность всех слов длины 10n+a.

11. Регулярно ли событие 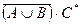, если A, B, C – регулярно.

12. Понятие регулярного множества.

13. Пусть а – автомат, А 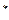- множество входных слов. Что можно сказать о множестве а(А )?

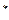Общерегулярные выражения и события.

1. Может ли общерегулярное событие состоять из одного сверхслова?

2. Привести пример одного сверхслова, не являющегося общерегулярным событием.

3. Является ли множество (всех) периодических сверхслов общерегулярным?

4. Привести пример сверхсобытия, непредставимого по Макноттону. Теорема Макноттона.

5. Общерегулярно ли множество всех периодических сверхслов с фиксированной длиной периода?

Тождественные преобразования.

1. Полная система тождеств. Конечность такой системы тождеств для .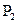

2. Конечна ли полная система тождеств для контактных схем.

3. Полная система тождеств для монотонных функций из .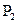

4. Пример класса без полной системы тождеств.

5. Существует ли полная конечная система тождеств для контактных схем и логических сетей?

Теория графов.

1. Какие классы графов можно раскрасить двумя цветами?

2. Теорема Шеннона о реберной раскраске (доказательство).

3. Доказательство непланарности .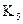

4. Теорема о разложении сетей.

5. Нелинейная нижняя оценка сложности числа деревьев.

Кодирование.

1. Найти ошибку в коде Хэмминга, исправляющем одну ошибку: 0000011101 (или 001001011).

2. Критерий Маркова в графовой форме.

3. Построить оптимальный код с заданными вероятностями.

4. Понятие равномерного кодирования.

5. Какую максимальную мощность имеет код, исправляющий одну ошибку при n=63?

6. L(n,m) – длина слов достаточная для однозначного декодирования входного алфавита мощности n словами из алфавита {0,1} длины m. Получить нижнюю оценку для L(n,m).