Обработка сообщений как кодирование

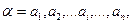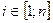Основные понятия теории кодирования. Словом в алфавите А называется кортеж, т.е. любая конечная последовательность символов где , число 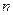показывает длину слова 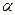и обозначается 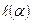.Пустое слово обозначается L, т.е. если L 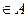, то = .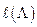

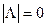Для слова 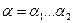буква a₁ называется началом или префиксом слова 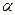, а буква 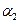– окончанием или постфиксом слова 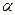. Пустое слово является началом и окончанием любого слова 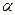, если 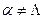. Для того, чтобы соединить слова, необходимо, чтобы префикс второго слова следовал сразу за постфиксом первого. Соединение слов a₁ и a₂ обозначается a₁a₂, соединение n одинаковых слов a обозначается 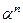, причем 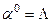. Множество всех непустых слов алфавита A обозначим A*, т.е. A*={a|l(a)>0}, в алфавите В – B*. Множество A называют алфавитом сообщений, а множество B – кодирующим алфавитом.

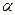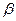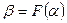Код сообщения (от лат. codex - называется) такое слово , что , где 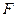– отображение всех слов алфавита А на алфавит В. Процесс F: A*®B* преобразования слов исходного алфавита A в алфавит B называется кодированием информации.Назовем элементарной частью сообщения ту его минимальную часть, которой ставится в соответствие символ из множества B.

Блочно-двоичный (m,n)-код.Слово длины m записывается с помощью двоичных символов 0 и 1. Сообщение длины m кодируется другим словом длины n, где m<n, которое передается по каналу связи.Если все кодовые слова имеют одинаковую длину, то код называется равномернымили блочным.

Алфавитное кодирование.Алфавитное, т.е. побуквенное кодирование задается таблицей кодов или схемой в виде подстановки 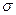. Из множества B* выбирается r слов b₁, b₂, …, b_r, называемых множеством элементарных кодов._.

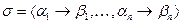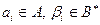Схема , где или 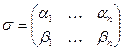задает алфавитное кодирование. Такое побуквенное кодирование обозначается .

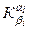Префиксной называется схема 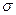, в которой элементарный код одной буквы не является префиксом кода другой буквы.

Разделимой называется схема 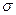, в которой любое слово, составленное из элементарных кодов, разлагается на элементарные коды единственным образом.

Проблема кодирования: возможность по коду b сообщения 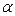однозначно восстановить это сообщение. Доказано, что если схема прямого кодирования 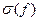и схема 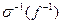обратного кодирования обладают свойством префикса, то соответствующее алфавитное кодирование будем взаимно-однозначным. Однако может случиться, что схема кодирования будет обладать свойством однозначности, но не будет обладать свойством префиксности (т.е. это лишь достаточное условие, оно не является необходимым).

Теорема А.А. Маркова (Критерий взаимной однозначности): Алфавитное кодирование со схемой s обладает свойством взаимной однозначности тогда и только тогда, когда в соответствующем графе отсутствуют контуры и петли, проходящие через вершину Λ. Т.о., алфавитное кодирование не является однозначным тогда и только тогда, когда соответствующий граф содержит ориентированный цикл (контур), проходящий через вершину Λ.

Для установления, обладает ли заданный код свойством однозначности, будем применять алгоритм:

1) Выпишем все нетривиальные разложения каждого элементарного кода.
2) Составим множество M₁, включая в него слова, входящие в качестве начал (префиксов) в нетривиальные разложения элементарных кодов.

3) Составим множество M₂, включая в него слова, которые являются окончаниями (постфиксами) нетривиальных разложений элементарных кодов.

4) Составим множество 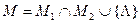, которое состоит из множества начал, окончаний нетривиальных разложений элементарных кодов.

5) Выпишем все разложения элементарных кодов, связанных с элементами множества M.

6) По полученным разложениям построим ориентированный граф, вершины которого – элементы множества 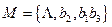. Пару вершин соединяем дугами тогда и только тогда, когда существует разложения, в которое вершины графа входят в качестве начала и конца.

7) Граф G подскажет, обладает ли заданная схема свойством однозначности. Для ответа на этот вопрос воспользуемся теоремой А.А. Маркова.

Алфавитное кодирование с разделимой схемой допускает декодирование. Для разделимой схемы 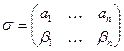алфавитного кодирования существует так называемая средняя цена или длина кодирования 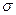, которая обозначается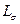и определяется 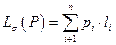где 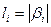– длина кодового слова, а 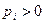– вероятность появления буквы .

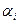Двоичное кодирование. Рассмотрим алфавит 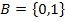и некоторое произвольное множество A, которое может быть некоторым конечным алфавитом, множеством слов в некотором алфавите. Множество слов длины n в этом алфавите обозначим Bⁿ.

Произвольное отображение множества A во множество слов алфавита B называют двоичным кодированием множества A. Код называется равномерным, если все буквы его алфавита имеют одинаковую длину.

Пусть Е - двоичная запись натуральных чисел. Кодирование E_k первых 2^k натуральных чисел, когда каждому n (где 0£n<2^k) ставится в соответствие слово e_k(n) – двоичная запись числа n с помощью k цифр. Код E_k является равномерным,т.к. у которого все буквы алфавита имеют длину, равную k.

n

e(n)

e4(n)

Методы эффективного кодирования информации.Наиболее выгодным является кодирование, на которое затрачивается минимальное количество символов (букв алфавита).

Алфавитное разделяемое кодирование будет кодированием с минимальной избыточностьюили оптимальным, если будут учтены распределения вероятностей p для символов этого алфавита.

Оптимальное кодирование. Последовательные появления букв алфавита А статистически независимы и подчинены распределению вероятностей .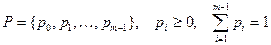

Каждый код b в алфавите В = {0, 1} характеризуется средним числом 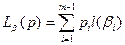двоичных цифр, приходящихся на одну букву алфавита А при побуквенном кодировании.