Решение логических задач с помощью таблиц истинности.
Задача.
А, В и С подозреваются в ограблении банка. Есть три версии:
- либо С ограбил банк, либо B или А ограбили банк;
- если С участвовал в ограблении, то А и B тоже участвовали;
- участие А в ограблении равносильно тому, что В участвовал, а С не участвовал.
Все версия оказались ложными. Кто ограбил банк?
РЕШЕНИЕ:
Обозначим
A=1  А ограбил банк.
А ограбил банк.
В=1  В ограбил банк.
В ограбил банк.
С=1  С ограбил банк.
С ограбил банк.
Составим формулы (версии):
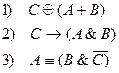
Построим таблицы истинности для каждой из формул и найдем строку, в которой все логические формулы принимают значение 0.
| A | B | С | С ⊕ (А+В) | С→(А&В) | А≡(В&C) |
Такая строка в таблице единственная – при значениях А = 1, В = 0, С = 1.
ОТВЕТ: А и С ограбили банк.
6.8 Понятия о комбинационных схемах и цифровых автоматах
Элементы ЭВМ выполняют функции простейших преобразователей информации. Они реализуют различные логические операции над сигналами входных двоичных переменных, а также обеспечивают запоминание, формирование и преобразование этих сигналов.
Функционально взаимосвязанные группы таких элементов образуют различные узлы ЭВМ, которые оперируют с многоразрядными двоичными кодами, например машинными словами или их частями. К числу типовых узлов ЭВМ относятся:
- регистры, обеспечивающие хранение и некоторое преобразование многоразрядных кодов;
- счетчики, предназначенные для подсчёта числа входных двоичных сигналов;
- дешифраторы, преобразующие входной многоразрядный код в сигнал на одном из выходов;
- сумматоры, выполняющие арифметическое суммирование двоичных кодов.
Элементы и узлы являются основой для построения других более сложных технических устройств ЭВМ. Вначале дадим общую характеристику элементной базы, которая не только определяет функциональные возможности различных узлов и устройств ЭВМ, но и отражает соответствующие этапы в развитии средств вычислительной техники .
Несмотря на огромное количество элементов, находящихся в составе ЭВМ, число их разновидностей (типов) относительно невелико. Это существенно упрощает процесс проектирования ЭВМ и повышает технологичность её изготовления. Типовой набор образует систему элементов ЭВМ, которая обладает общими электрическими, конструктивными и технологическими свойствами, использует однотипные связи между элементами, совместимые по своим входным и выходным параметрам.
Устройство ЭВМ, преобразующее двоичную информацию, в общем случае представляется многополюсником с n входами и m выходами. На его входы поступают входные двоичные сигналы xi (i = 1, 2, …, n), а с выхода снимаются выходные сигналы yj (j = 1, 2, …, m).
В любой момент времени наборы этих сигналов образуют соответственно входное слово X (х1, х2, …, хn) и выходное слово Y (у1, у2, …, уm).
Преобразование информации в ЭВМ производится логическими устройствами двух классов: комбинационными схемами и цифровыми автоматами.


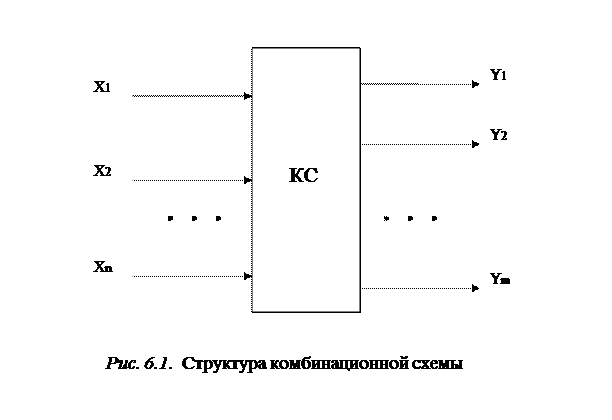
В комбинационной схеме (КС) набор выходных сигналов (выходное слово Y) в любой момент времени полностью определяется набором входных сигналов (входным словом X), поступающих в тот же момент (рис. 6. 1). Таким образом, в КС результат обработки информации зависит только от комбинации входных сигналов и вырабатывается одновременно с их поступлением.
Закон функционирования комбинационной схемы полностью определен, если задано соответствием между её входными и выходными словами, например, в виде таблицы. По этой таблице можно получить аналитическую форму зависимости выходных и входных слов КС с использованием соответствующих логических функций (например, в ДСНФ или КСНФ).
Техническая реализация комбинационных схем производится логическими элементами, каждый из которых воспроизводит ту или иную логическую функцию двоичных переменных. Набор таких элементов должен обеспечивать реализацию функционально полной системы логических функций. В процессе логических устройств ЭВМ необходимо стремиться к минимальному числу и однородности используемых логических элементов.


Цифровые автоматы
Термин автомат как правило используется в двух аспектах. С одной стороны, автомат – устройство, выполняющее некоторые функции без непосредственного участия человека. С другой стороны, термин «автомат» как математическое понятие обозначает математическую модель реальных технических автоматов. В этом аспекте автомат представляется как «чёрный ящик», имеющий конечное число входов и выходов и некоторое множество внутренних состояний, в которые он под воздействием входных сигналов переходит скачкообразно, практически мгновенно, минуя промежуточное состояние.
Автомат называется конечным, если множество его внутренних состояний и множество входных сигналов – конечные множества.
В цифровых автоматах набор выходных сигналов Y (y1, y2, …, ym) зависит не только от набора входных сигналов X (x1, x2, …, xn), но и от внутреннего состояния Q (q1, q2, …, qk) данного устройства (рис. 6.2).
Цифровые автоматы имеют память, фиксирующую состояние автомата. Наборы переменных X, Y и Q называются соответственно входным, выходным и внутренним алфавитами. Обычно значения этих алфавитов разделяют по временным интервалам t = 0, 1, 2, …, называемым тактами. В течение такта состояние всех трёх алфавитов сохраняются неизменными.
Цифровой автомат называется правильным, если выходной сигнал определяется только его внутренним состоянием и не зависит от входного сигнала.
Пусть имеется автомат с одним входом . Математической моделью цифрового автомата является абстрактный автомат, заданный совокупностью шести объектов:
- конечное множество входных сигналов Х;
- конечное множество выходных сигналов Y;
- произвольное множество Q состояний автомата;
- начальное состояние автомата q0, как элемент множества Q;
- функция перехода автомата из одного состояния в другое;
- функция выходов автомата.
Закон функционирования цифрового автомата однозначно определен, если установлены связи во времени между его алфавитами. С этой целью обычно задают в виде таблицы или в аналитической форме функции переходов и выходов
Qt+1 = φ(Qt, Xt);
Yt = ψ (Qt, Xt),
которые определяют зависимости соответственно состояние автомата Qt+1 и выходного слова Yt от состояния автомата Qt и входного слова Xt. При этом должно быть указано начальное состояние автомата q0.
В теории автоматов наиболее полно описаны синхронные автоматы.
В зависимости от способа определения выходного сигнала в синхронных автоматах существуют две возможности:
- выходной сигнал однозначно определяется входным сигналом и внутренним состоянием автомата в предшествующий момент (автоматы Мили);
- выходной сигнал однозначно определяется входным сигналом и внутренним состоянием автомата в данный момент времени.
Автомат, для которого выходное слово Yt в такте t зависит только от состояния автомата Qt в этом такте и не зависит от входного слова Xt, называет автоматом Мура. Для него функция выходов имеет вид Yt = ψ (Qt).
При построении устройств ЭВМ, являющихся цифровыми автоматами, наряду с комбинационными логическими элементами применяются элементы памяти, в качестве которых используются элементарные автоматы Мура с двумя устойчивыми состояниями, обладающие полными системами выходов и переходов. Причем автомат Мура имеет полную систему выходов в том случае, если для каждого его состояния выходные сигналы различны и полную систему переходов в том случае, если для любых состояний автомата всегда имеется входной сигнал, который переводит автомат из одного состояния в другое.
Напомним, что комбинационные схемы выполняют логические операции над наборами входных двоичных переменных, причем результат этих операций зависит только от комбинации входных переменных и вырабатывается сразу после их поступления. Цифровые автоматы обладают некоторым числом внутренних дискретных состояний, поэтому их выходные сигналы зависят не только от комбинации входных переменных, но и от
состояния автомата.
Техническая реализация цифровых устройств этих двух классов требует использования соответствующих элементов. Комбинационные схемы выполняются на логических элементах; цифровые автоматы кроме логических элементов используют также запоминающие элементы, которые фиксируют их внутренние состояния.
Дадим общую характеристику логическим и запоминающим элементам ЭВМ.
Логические элементы обеспечивают реализацию различных логических функций от входных двоичных переменных, например функций И, ИЛИ
и НЕ. Названные функции образуют функционально полный набор, поэтому с помощью таких элементов можно построить любые сложные комбинационные схемы. Однако в ряде случаев проще реализовать некоторые логические схемы с использованием более сложных логических элементов, например элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ, каждый из которых также образует функционально полный набор, обеспечивающий построение любых комбинационных схем.
В табл. 6.7. приведены условные обозначения некоторых типовых логических элементов и реализуемые ими логические функции. Выход элемента обозначается кружком, если им реализуется функция с инверсией (отрицанием); вход также отмечается кружком, если функция реализуется при инверсном значении соответствующей входной переменной.
Таблица 6.7. Графические изображения комбинационных схем
| Наименование элемента | Условное обозначение | Название и логическая запись функции |
| И | 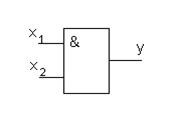 | Конъюнкция: y=x1&x2 y=x1x2 |
| ИЛИ | 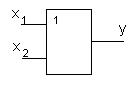 | Дизъюнкция: y=x1Vx2 y=x1+x2 |
| НЕ | 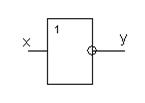 | Инверсия: y=x y = x |
| ИЛИ-НЕ | 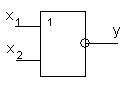 | Стрелка Пирса: ______ y=x1Vx2 y=x1↑x2 |
| И-НЕ | 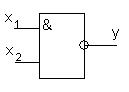 | Штрих Шеффера: ____ y=x1x2 y=x1/x2 |
Логические элементы обычно выпускаются в виде микросхем малой и средней степени интеграции, в которых реализуются разнообразные совокупности логических операций, таких, как И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ и др.
Запоминающие элементы выполняют функцию памяти для двоичных переменных 0 и 1, для чего они должны иметь два устойчивых состояния равновесия, одно из которых принимается за «0», а другое за «1». Каждому из этих состояний соответствуют различные выходные сигналы. В запоминающих элементах с помощью входных сигналов устанавливается необходимое состояние, которое сохраняется неизменным после прекращения действия этих сигналов. Указанным требованиям отвечают так называемые триггеры, реализуемые в виде полупроводниковых микросхем различной степени интеграции. Существует несколько различных типов триггеров. Большинство из них применяется для построения узлов ЭВМ, например регистров, счетчиков, некоторых сумматоров и др. Триггеры, выполненные на больших интегральных схемах (БИС), используются также в полупроводниковых запоминающих устройствах (БИС ЗУ). Обычно в каждом корпусе БИС ЗУ размещается несколько тысяч запоминающих элементов.
Как уже отмечалось, при проектировании узлов и устройств ЭВМ используется та или иная система элементов, в которую наряду с логическими и запоминающими элементами входят и вспомогательные элементы, обеспечивающие усиление и генерацию информационных сигналов, а также их преобразование по мощности, амплитуде или длительности. Помимо функциональной полноты система элементов ЭВМ обладает общностью и совместимостью технических и эксплуатационных характеристик.
С развитием вычислительной техники постоянно улучшаются и совершенствуются параметры и характеристики элементов ЭВМ.
В качестве примера рассмотрим описание работы узла ЭВМ, называемого сумматором.
Определение:
Узел ЭВМ, выполняющий арифметическое суммирование кодов чисел, называется сумматором.
Операция суммирования осуществляется в сумматорах поразрядно с использованием одноразрядных суммирующих схем. При этом в каждом разряде требуется выполнить сложение трех двоичных цифр: цифры данного разряда первого слагаемого xi,
цифры этого же разряда второго слагаемого yi и цифры переноса Pi из соседнего младшего разряда.
Иногда такое суммирование разбивают на две аналогичные операции: суммирование двух цифр слагаемых и суммирование полученного результата
с переносом из соседнего младшего разряда. Каждая из этих операций выполняется схемой, называемой полусумматором. В табл. 6.7. приведена логика работы сумматора на два входа: хi и yi. На его выходах образуется сумма Si данного разряда и осуществляется перенос Рi+1 в следующий старший разряд. По таблице можно составить логические выражения
для суммы Si и переноса Рi+1:
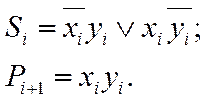
Преобразуем выражение для суммы Si к виду
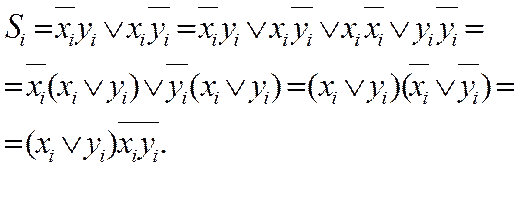
|
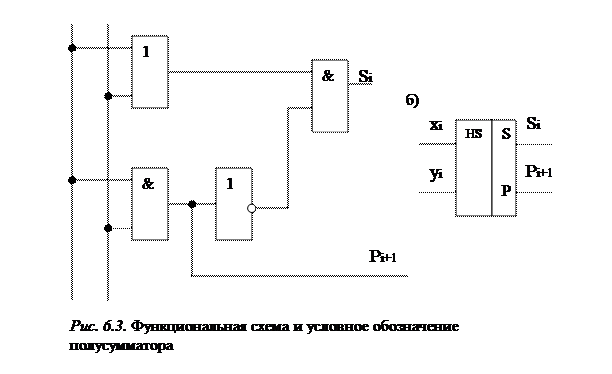
На рисунке 6.3. a,b приведены функциональная схема полусумматора, составленная в соответствии с полученными логическими выражениями, и его условное графическое обозначение.
Таблица 6.7. Описание работы сумматора на два входа
| Xi | yi | Si | Pi+1 |
Опишем коротко назначение оставшихся функциональных узлов.
Регистры.
Функциональный узел ЭВМ, предназначенный для запоминания многоразрядных кодов и выполнения над ними некоторых логических преобразований называется, регистром. Регистр включает в себя отдельные триггеры, количество которых соответствует количеству разрядов двоичного кода двоичного кода, а также вспомогательные схемы, обеспечивающие приём кода в регистр, передачу кода в другой регистр, сдвиг кода и т.д.
Регистр процессора — встроенная сверхбыстрая оперативная память (СОЗУ) процессора, предназначенная для хранения промежуточных результатов вычисления (регистр общего назначения) или содержащая данные, необходимые для работы самого процессора (специальные регистры). Регистр представляет собой цифровую электронную схему, служащую для временного хранения двоичных чисел.
Большая часть регистров процессора используется для внутренных целей и недоступна программисту. Есть регистры, которые в принципе программно доступны, но предназначены только для использования системными программами. Существуют также регистры, свободно использующиеся в вычислительных операциях (регистры общего назначения).
Пользовательские регистры. Эти регистры позволяют программисту сократить число обращений к основной памяти, оптимизируя использование регистров с помощью машинного языка или ассемблера. В состав языков высокого уровня входят оптимизирующие компиляторы, построенные на алгоритмах, которые, в частности, позволяют определить, какие переменные следует заносить в регистры, а какие — в основную память. Некоторые языки высокого уровня, такие, как С, предоставляют программисту возможность предложить компилятору хранить те или иные данные в регистрах.
Регистры управления и регистры состояния. Используются в процессоре
для контроля над выполняемыми операциями; с их помощью привилегированные программы операционной системы могут контролировать ход выполнения других программ.
Счётчики.
Функциональный узел, предназначенный для подсчёта числа входных сигналов и запоминания кода этого числа соответствующими триггерами, называется счётчиком.
Дешифраторы.
Комбинационная логическая схема, преобразующая поступающий на входы код в сигнал только на одном из её выходов, называется дешифратором. Если количество двоичных разрядов дешифруемого кода обозначить через n, то число выходов дешифратора должно быть 2n.
В заключение главы рассмотрим примеры представления логических функций в базисах: 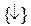 - базис Пирса (элемент Вебба);
- базис Пирса (элемент Вебба);
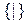 - базис Шеффера;
- базис Шеффера;
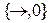 - импликативный базис;
- импликативный базис;
{→,↛}- импликация, коимпликация;
Пример 1.
Рассмотрим представление логических функций в базисе Шеффера.
А|В = 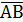 =
= 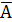 +
+ 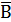
1. АВ =  =
= 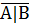 = (А|В) | (А|В)
= (А|В) | (А|В)
Проверим результат с помощью таблицы истинности:
| А | В | А|В | (А|В) | (А|В) |
2. А + В = 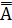 +
+ 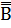 =
= 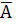 |
| 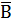 = (А|А) | (В|В)
= (А|А) | (В|В)
Результат проверить самостоятельно.
3. Логическая функция задана формулой 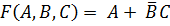 .
.
Представить заданную функцию в базисе Шеффера.
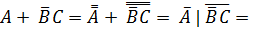 (А|А) | (
(А|А) | ( 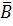 |C) = (А|А) | ((В|В)|C)
|C) = (А|А) | ((В|В)|C)
4. Логическая функция задана таблицей истинности: 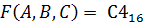 .
.
Представить заданную функцию в базисе Шеффера. Построить комбинационную схему для функции 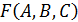 , представленной в базисе Шеффера.
, представленной в базисе Шеффера.
Решение.
1. Построим СДНФ для заданной функции:
| А | В | С | 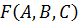 | Элементарные минтермы |
| 1* | 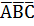 | |||
| 1* | 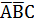 | |||
| 1* | 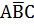 | |||
СДНФ: 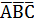 +
+ 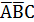 +
+ 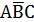 .
.
2. Упростим полученную формулу, после упрощения выполним проверку:
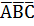 +
+ 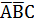 +
+ 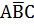 =
= 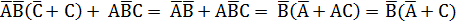
Проверка:
| А | В | С | 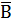 | 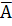 | 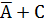 | 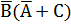 |
3. Выразим функцию 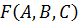 в базисе Шеффера:
в базисе Шеффера:
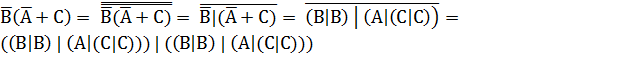 .
.
Выполним проверку:
| А | В | С | В|В | С|С | А|(С|С) | (В|В) |(А|(С|С)) | F(A,B,C) |
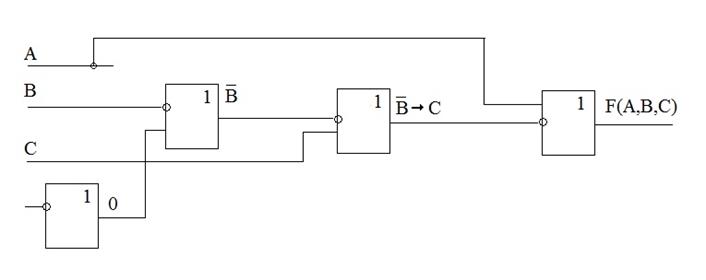
4. Построение комбинационной схемы.
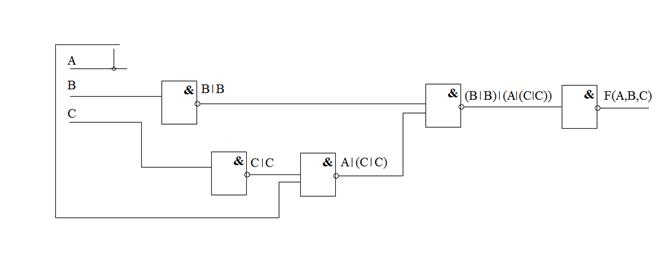
Пример 2.
Представить логическую функцию F(A,B,C) = 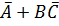 в базисе стрелка Пирса.
в базисе стрелка Пирса.
Предварительно рассмотрим, как выражаются конъюнкция и дизъюнкция через базис стрелка Пирса.
A↓B = 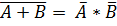
1. AB = 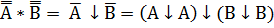
2. А+В= 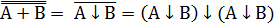
3. 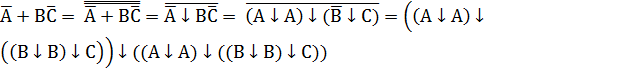
Проверку выполнить самостоятельно.
Для того чтобы выполнить проверку постройте таблицу истинности исходной функции и функции, представленной в базисе стрелка Пирса.
Пример 3.
Представить логическую функцию F(A,B,C)=А+ 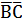 в базисе {→, 0}. Построить комбинационную схему для функции, выраженной в базисе {→, 0}.
в базисе {→, 0}. Построить комбинационную схему для функции, выраженной в базисе {→, 0}.
Рассмотрим представление отрицания, конъюнкции и дизъюнкции в базисе {→, 0} :
1. 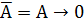
2. А*В = А* 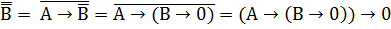
Выполним проверку:
| А | В | В 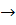 0 0 | 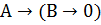 | 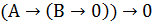 |
3. А+В = А+ 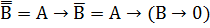
4. А+ 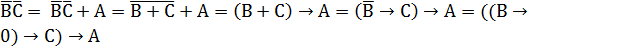
Пример 4.
Логическая функция F(A,B,C) задана таблицей истинности F(A,B,C)=В3.
Получить аналитическое представление функции в базисе {→,↛}.
Решение.
1. Получим отрицание в базисе {→,↛}. Для этого необходимо получить константу 0 или 1.
1 способ: получаем константу 0.
а) 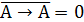
б) 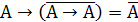
2 способ: получаем константу 1.
а) 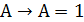
б) 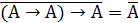
Следующие действия выполнит самостоятельно:
- получить СКНФ;
- раскрыть скобки, упростить выражение;
- записать формулу, используя операцию отрицания;
- заменить операцию отрицания , записанную в явном виде на действия, перечисленные либо в способе 1, либо в способе 2.
