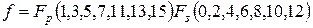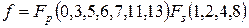Табличные методы минимизации функций
Алгебры логики
3.3.1. Минимизация ФАЛ с помощью матрицы Карно
Матрица Карно представляет собой своеобразную таблицу истинности ФАЛ, которая разбита на клетки. Количество клеток матрицы равно 2n, где n – число аргументов ФАЛ. Столбцы и строки матрицы обозначаются наборами аргументов. Каждая клетка матрицы соответствует конституэнте единицы ФАЛ (двоичному числу). Двоичное число клетки состоит из набора аргументов строки и столбца. Матрица Карно для ФАЛ, зависящей от двух аргументов, представлена в виде таблицы 3.3., от трех аргументов таблицей 3.4. и от четырех аргументов таблицей 3.5.
Таблица 3.3.
| х2 х1 | ||
| 0 0 | 0 1 | |
| 1 0 | 1 1 |
Таблица 3.4.
| х2х3 х1 | ||||
| 0 0 0 | 0 0 1 | 0 1 1 | 0 1 0 | |
| 1 0 0 | 1 0 1 | 1 1 1 | 1 1 0 |
Таблица 3.5.
| х3х4 х1х2 | ||||
| 0 0 0 0 | 0 0 0 1 | 0 0 1 1 | 0 0 1 0 | |
| 0 1 0 0 | 0 1 0 1 | 0 1 1 1 | 0 1 1 0 | |
| 1 1 0 0 | 1 1 0 1 | 1 1 1 1 | 1 1 1 0 | |
| 1 0 0 0 | 1 0 0 1 | 1 0 1 1 | 1 0 1 0 |
Клетки матриц (таблицы 3.3., 3.4. и 3.5.) пронумерованы десятичными эквивалентами двоичных чисел клеток. Рядом расположенные клетки матриц, как по горизонтали, так и по вертикали, содержат соседние двоичные числа. Кроме этого соседние двоичные числа находятся во всех столбцах верхней и нижней строк, так же как во всех строках крайних столбцов.
Процесс минимизации ФАЛ с помощью матрицы Карно основан на законе склеивания соседних двоичных чисел. Можно склеивать двоичные числа рядом расположенных клеток, но рекомендуется склеивать наборы аргументов, которыми обозначены строки и столбцы матриц. Рассмотрим склеивание двоичных чисел клеток первого столбца матрицы (табл. 3.5.).
Клетки 0 и 4, соответственно двоичные числа 0000 и 0100, результат склеивания 0-00.
Клетки 8 и 12, двоичные числа 1000 и 1100, результат 1-00. Полученные импликанты склеиваются между собой, т.к. тире стоит в одном и том же разряде и двоичные числа импликант являются соседними, окончательный результат - - 00.
| 0 - 0 0 |
| 1 - 0 0 |
| - - 0 0 |
Обратим внимание на то, что такой же результат получим, если будем склеивать двоичные числа, которыми обозначены строки матрицы.
Клетки 0 и 4
| 0 0 |
| 0 1 |
| 0 - |
Клетки 8 и 12
| 1 1 |
| 1 0 |
| 1 - |
Результат
| 1 - |
| 0 - |
| - - |
Таким образом, если склеиваются все двоичные числа одного столбца, то пропадают те разряды, которыми обозначены строки. Аналогично, если будут склеиваться все двоичные числа одной строки, например 4, 5, 7, 6, то пропадают все разряды, которыми обозначены столбцы, т.е. результат будет следующий 01- -.
Если будут склеиваться двоичные числа только двух любых клеток, то прочерк ставиться вместо того разряда двоичных чисел строки или столбца, который изменится при переходе клеток из одной строчки в другую (или из одного столбца в другой). Например, склеиваются числа клеток 5 и 13, получим результат -101, или клеток 7 и 6 результат 011-.
При склеивании двоичных чисел восьми рядом расположенных клеток пропадает три переменные, например для клеток 3, 7, 15, 11, 2, 6, 14, 10 пропадают переменные х1, х2, х3. Переменные х1, х2 пропадают потому, что склеиваются все клетки столбцов, а х3 потому, что последние два столбца склеиваются между собой.
Прежде, чем рассмотреть примеры минимизации ФАЛ с помощь матрицы Карно, необходимо дать классификацию наборов аргументов, с помощью которых определяются функции алгебры логики.
Известно, что для каждой ФАЛ имеет место количество наборов аргументов 2n, где n – число аргументов от которых зависит функция или логическое выражение.
Наборы аргументов делятся на три вида
1. Наборы аргументов, на которых функция равна единице, называются рабочими.
2. Наборы аргументов, на которых функция равна нулю, называются запрещенными.
3. Наборы аргументов, на которых функция может быть равна или единице, или нулю, называются безразличными.
Если заданная ФАЛ не имеет безразличных наборов, то она может быть представлена в буквенном выражении в виде СДНФ. При наличии в заданной ФАЛ безразличных наборов, ее представление может иметь следующую форму.
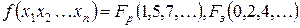 ,
,
где 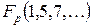 – десятичные эквиваленты рабочих наборов,
– десятичные эквиваленты рабочих наборов,
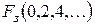 – десятичные эквиваленты запрещенных наборов.
– десятичные эквиваленты запрещенных наборов.
Наборы аргументов, которых нет среди рабочих и запрещенных, будут безразличными.
Пример 3.3. Минимизировать заданную ФАЛ в виде СДНФ с помощью матрицы Карно 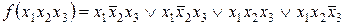 .
.
Следовательно, функция задана только рабочими наборами. Остальные будут запрещенными. Функция зависит только от трех аргументов. Строим матрицу Карно и в ее клетках, которые соответствуют рабочим наборам ставим единицы, а в остальных клетках ставим нули.
Таблица 3.5.
| х2х3 х1 | ||||
 0 0 | ||||
Для минимизации клетки матрицы, в которых стоят единицы, объединяются в контуры. В контур могут включаться две клетки, четыре или все восемь. В данном примере в контур включены четыре рядом расположенные клетки одной строки. Импликантой заданного контура будет 1 - -. Результат минимизации следующий 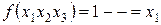 , т.е. произошло сокращение заданной функции в СДНФ на 11 букв.
, т.е. произошло сокращение заданной функции в СДНФ на 11 букв.
Пример 3.4. Минимизировать логическое выражение, заданное рабочими и запрещенными наборами с помощью матрицы Карно.
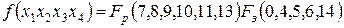
Строим матрицу Карно на четыре переменных и заполним клетки единицами и нулями соответственно для рабочих и запрещенных наборов.
Таблица 3.6.
| х3х4 х1х2 | 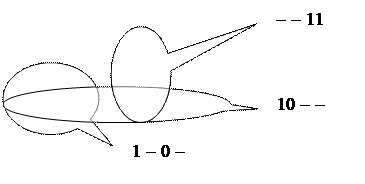 00 00 | |||
| (1) | ||||
| (1) | (1) | |||
При объединении клеток с единицами в контуры желательно, чтобы в каждый контур включалось наибольшее число клеток из максимально возможного. Для этого клетки некоторых безразличных наборов используем как клетки рабочих наборов, подставив в них единицы в скобках. В результате получим три контура, содержащие по 4 клетки. В обобщенном коде контура, включающего в себя все клетки одной строки, пропадают переменные х2х3 (10 - -). В обобщенном коде контура, включающего все клетки одного столбца пропадают переменные х1х2 (- - 11) и для контура, содержащего по две клетки двух строк пропадают переменные х2 (при переходе в контуре из одной строки в другую) и х3 (при переходе из одного столбца в другой). В результате получим минимальную ДНФ в следующем виде
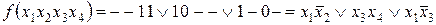 .
.
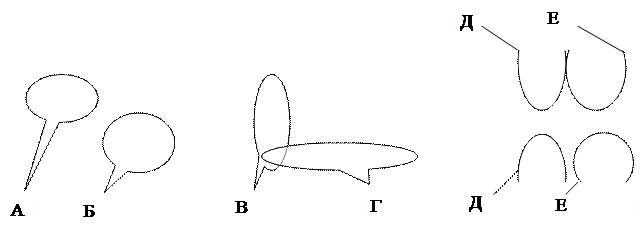
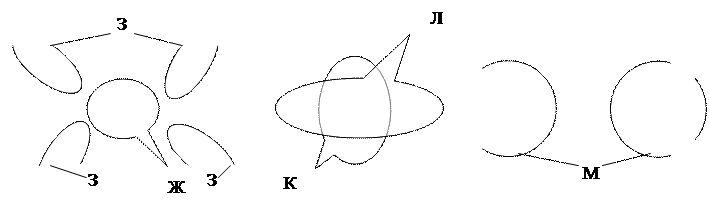
Возможные варианты объединения клеток матрицы Карно в контуры показаны на рисунке 3.4.
 х3х4 х1х2 х3х4 х1х2 | ||||||||||||||||

| А = 0 - 0 - | З = - 0 - 0 | |||||||||||||||
| Н | Б = 1 - 1 - | К = - - - 1 | ||||||||||||||
| В = - - 0 0 | Л = - 1 - - | |||||||||||||||
| Г = 1 0 - - | М = - - - 0 | |||||||||||||||
| Д = - 0 0 1 | Н = - 0 - - | |||||||||||||||
| Е = - 0 1 - | ||||||||||||||||
| Ж = - 1 - 1 |
Рис. 3.1. Возможные варианты объединения клеток матрицы Карно в контуры
3.3.2. Минимизация функций алгебры логики с помощью матрицы на пять переменных
Матрица минимизации на пять переменных строится аналогично матрице Карно, т.е. в этой матрице рядом расположенные столбцы и строки должны быть обозначены соседними двоичными числами наборов переменных
В матрице на пять переменных (таблица 3.7.) строкам соответствуют наборы переменных х1х2х3, а столбцам наборы переменных х4х5. Каждой клетке матрицы соответствует пятиразрядное двоичное число. В клетках матрицы (табл. 3.7.) проставлены десятичные эквиваленты соответствующих двоичных чисел.
Таблица 3.7.
| х4х5 х1х2х3 | ||||
Минимизация ФАЛ с помощью матрицы на пять переменных заключается в объединении клеток с рабочими наборами (включая при необходимости и клетки с безразличными наборами) в контуры и получении для этих контуров соответствующих им обобщенных кодов.
Особенность здесь заключается в том, что в столбцах матрицы на пять переменных объединять по четыре клетки в контуры можно только или четыре клетки сверху, или четыре клетки внизу, или четыре клетки посередине. Например, для последнего столбца матрицы контуры могут состоять из клеток 2, 6, 14, 10, или 26, 30, 22, 18 или 14, 10, 26, 30.
Пример 3.6. Минимизировать с помощью матрицы на пять переменных следующее логическое выражение
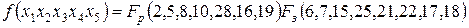
Строим матрицу на пять переменных и заполняем клетки рабочих наборов единицами, запрещенных – нулями.
Объединяем в контуры клетки с рабочими наборами, включая в них необходимые клетки безразличных наборов. Для каждого контура определяем обобщенных код.
Таблица 3.8.
х4х5 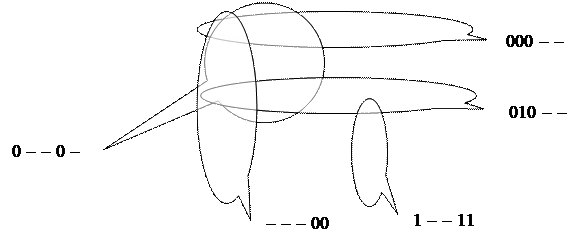 х1х2х3 х1х2х3 | ||||
| (1) | (1) | (1) | ||
| (1) | ||||
| (1) | (1) | |||
| (1) | (1) | |||
| (1) | (1) | |||
| (1) | ||||
| (1) | (1) | |||
Получаем минимальную ДНФ
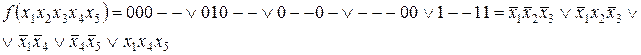
Контрольные вопросы
1. Дать определение сокращенной ДНФ.
2. Что представляет собой тупиковая ДНФ?
3. Как выбирается минимальная ДНФ из тупиковых ДНФ?
4. Для чего используется импликантная таблица и как она строится?
5. Пояснить аналитический способ минимизации ФАЛ Квайна-Мак-Класски.
6. Как строится матрица Карно на три и четыре переменных?
7. Минимизировать аналитическим способом следующие логические выражения, заданные только рабочими наборами
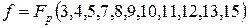
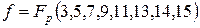
8. Минимизировать с помощью матрицы Карно логические выражения, заданные рабочими и запрещенными наборами