Частично-рекурсивные и вычислимые функции
Алгебра логики.
1. Существует ли булева функция, максимальные интервалы которой пересекаются следующим образом 
?
2. Всегда ли длина минимальной днф минимальна.
3. Если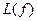 
сложность минимальной ДНФ функции 
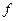, то найти 
.
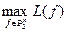4. Может ли быть в полиноме Жегалкина несущественная переменная?
5. Существует ли функция, принадлежащая одному из пяти предполных классов в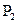 
и не принадлежащая остальным?
6. Сколько минимальных ДНФ у линейных и монотонных функций?
7. Известно, что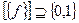 
. Вопрос: полно ли 
?
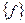8. Пример ДНФ, являющейся кратчайшей, но не минимальной.
9. Привести пример функций, на которых доказывается не локальность ДНФ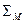 
.
10. Как строить минимальную ДНФ для монотонной функции?
11. Критерий полноты в классе монотонных функций в 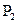. Найти классы, предполные в 
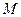, базис.
12. Пересечение всех замкнутых классов в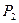 
.
13. Пересечение всех предполных классов в .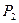
14. Построить конечную полную систему тождеств для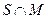 
над базисом 
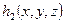(функция голосования).
15. Доказать, что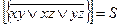 
.
16. Конъюктивная нормальная форма. Поможет ли в поиске минимальной КНФ знание минимальной ДНФ для конкретной функции?
17. Критерии полноты в предполных классах.
18. Как связаны монотонные и антимонотонные функции? Замкнуты ли антимонотонные функции?
19. Когда сокращённая и совершенная ДНФ монотонной функции совпадают?
20. Пусть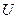 
-д.н.ф., 
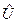-д.н.ф., полученная из 
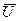. Как связаны 
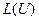и 
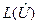, где 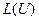-сложность д.н.ф.
21. Для функции f(x1,…,xn) известны все её минимальные ДНФ. Описать минимальные ДНФ для функции f(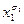 
,…, 
).
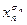Многозначная логика.
1. Конечно ли число предполных классов в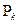 
?
2. Оценить (как-нибудь) число предполных классов в .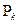
3. Вычислить пересечение всех предполных классов в .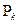
4. Полна ли в 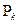система функций 
?
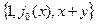5. 
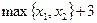Шеферова в 
, 
?
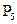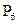6. Возможно ли равенство: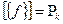 
?
7. 
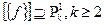. Когда 
?
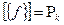8. Будет ли полна в 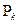система, состоящая из одной функции, если ее замыкание содержит все одноместные функции?
9. Верно ли утверждение, что система, содержащая все одноместные функции, принимающие не более k-2 значения и существенную функцию, полна?
10. Выразить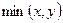 
через систему функций 
.
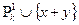11. В любом ли 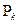имеются нелинейные функции?
12. 
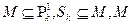предполно в 
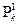. Описать . ( 
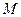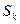множество перестановок).
13. 
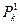- множество всех одноместных функций, принимающих не более k-1 значения. Верно ли утверждение, что 
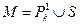полно тогда и только тогда, когда S содержит существенную функцию.
14. 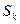предполный класс в 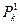или нет?
15. Дано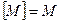 
и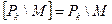 
. Найти все такие M.
16. Дано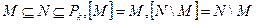 
. Какие могут быть M и N?
17. Существуют ли в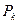 
замкнутые классы с бесконечным базисом?
18. Полна ли система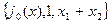 
в ?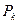
19. При каких k в 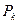любую функцию можно представить полиномом по модулю k?
20. Каковы ширина и глубина решётки замкнутых классов в Рк?
21. М0 – класс в Рк сохраняющий 0. Показать, что М0 предполный.
22. 
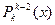- множество всех функций из 
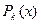, принимающих не более k-2 значений. Полна ли система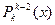 
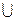{f}, где f – существенная функция? (k=3 и k=4).
23. Если класс H конечнопорождённый в Рк, то всегда ли найдётся в нём предполный класс?
24. Пусть 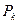– класс всех полиномов по mod k. Верно ли утверждение 
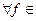Рк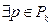 
: 
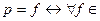Рк (x) : 
?
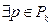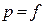Частично-рекурсивные и вычислимые функции.
1. Пример не всюду определенной частично-рекурсивной функции.
2. Вычислимость функции, растущей быстрее любой вычислимой функции.
3. Пример невычислимой функции.
4. Понятие частично-рекурсивной функции.
5. Можно ли произвольную частично-рекурсивную функцию доопределить до общерекурсивной?
6. Пример невычислимой всюду определенной функции.
7. Может ли функция, принимающая 2 (n) значения, быть невычислимой?
8. Существует ли функция, растущая быстрее, чем любая одномерная вычислимая функция?
9. Сузится ли класс рекурсивных функций, если выбросить операцию примитивной рекурсии?
10. Понятие алгоритма.
11. Моделирование автомата машиной Тьюринга.
12. Существует ли алгоритм проверки однозначности декодирования, если отображение, задающее кодирование, задается алгоритмом?
13. Существует ли не всюду определенная примитивно-рекурсивная функция?
14. Существует ли универсальная общерекурсивная функция для класса общерекурсивных?
15. Показать, что усеченная разность является примитивно-рекурсивной.
Автоматы.
1. Примеры автоматов, на которых достигаются оценки Мура.
2. Понятие однородной структуры.
3. Число неизоморфных автоматов, имеющих два входа, два состояния и один выход.
4. Определение магазинного автомата.
5. Автоматы Мура, Медведева, Мили.
6. Написать канонические уравнения для автомата, заданного логической сетью и диаграммой Мура.
7. Полна ли в классе ограниченно-детерминированных функций система:
{штрих Шеффера, 
}?
8. Базис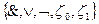 
с какой сложностью может быть реализована автоматная схема с n входами, m выходами и p состояниями, если все элементы имеют сложность 1?
9. Сколько состояний у задержки. Написать канонические уравнения задержки.
10. 
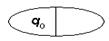- множество состояний автомата. Регулярно ли множество входных слов, заставляющих не более одного раза зайти в правую часть и вернуться?
11. Как связаны длины периодов входных и выходных слов автомата?
12. Привести пример универсальной однородной структуры.
13. Написать канонические уравнения для автомата:
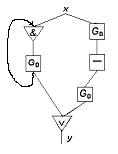
14. Существует ли полная система для автоматов вида:
а)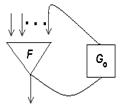 
и б)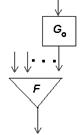 
, где функция F из Р2.
15. Можно ли все автоматы Мура получить из автомата вида:
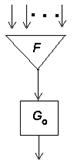, где функция F из Р2.
16. Построить автомат, представляющий а(А 
), где а:
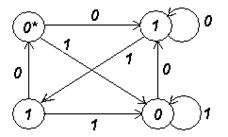
17. Автомат В обратный к автомату А, если 
есть тождественный автомат (входной и выходной алфавиты – {0,1}). Когда для А существует обратный?
18. А=В={0,1} – входной и выходной алфавиты автомата а. Можно ли распознать свойство а(А )= А ?