Структура данных системы нечеткого логического вывода

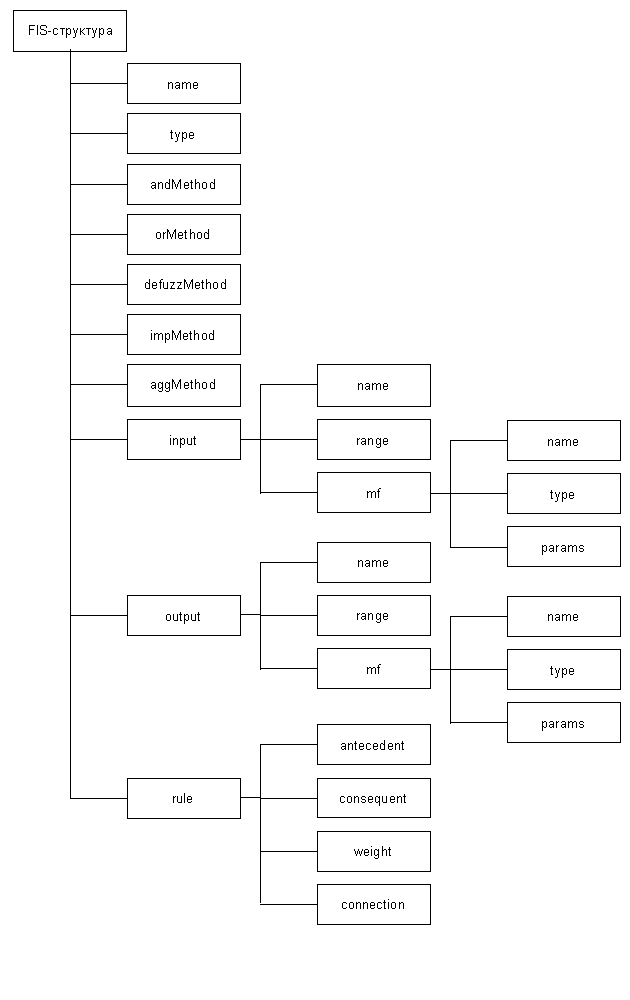
Система нечеткого логического вывода представляется в рабочей области MatLab в виде структуры данных, изображенной на рис. 5.1.

Существует два способа загрузки FIS в рабочую область:

• считывание с диска с помощью функции readfis;
• передача из основного fis-редактора путем выбора в меню File подменюExportи команды To workspace.

Поля структуры данных системы нечеткого логического вывода предназначены для хранения следующей информации:

name	-	наименование системы нечеткого логического вывода;
type	-	тип системы. Допустимые значения 'Mamdani' и 'Sugeno';
andMethod	-	реализация логической операции И. Запрограммированные реализации: 'min' - минимум и 'prod' - умножение;
orMethod	-	реализация логической операции ИЛИ. Запрограммированные реализации: 'max' - максимум и 'probor' - вероятностное ИЛИ;
defuzzMethod	-	метод дефаззификации. Запрограммированные методы для систем типа Мамдани: 'centroid' - центр тяжести; 'bisector' -медиана; 'lom' - наибольший из максимумов; 'som' - наименьший из максимумов; 'mom' - среднее из максимумов. Запрограммированные методы для систем типа Сугэно: 'wtaver' - взвешенное среднее и 'wtsum' - взвешенная сумма;
impMethod	-	реализация операции импликации. Запрограммированные реализации: 'min' - минимум и 'prod' - умножение;
aggMethod	-	реализация операции объединения функций принадлежности выходной переменной. Запрограммированные реализации: 'max' - максимум; 'sum' - сумма и 'probor' - вероятностное ИЛИ;
input	-	массив входных переменных;
input.name	-	наименование входной переменной;
input.range	-	диапазон изменения входной переменной;
input.mf	-	массив функций принадлежности входной переменной;
input.mf.name	-	наименование функции принадлежности входной переменной;
input.mf.type	-	модель функции принадлежности входной переменной. Запрограммированные модели: dsigmf - функция принадлежности в виде разности между двумя сигмоидными функциями; gauss2mf - двухсторонняя гауссовская функция принадлежности; gaussmf - гауссовская функция принадлежности; gbellmf - обобщенная колокообразная функция принадлежности; pimf - пи-подобная функция принадлежности; psigmf - произведение двух сигмоидных функций принадлежности; sigmf - сигмоидная функция принадлежности; smf - s-подобная функция принадлежности; trapmf - трапециевидная функция принадлежности; trimf - треугольная функция принадлежности; zmf - z-подобная функция принадлежности;
input.mf.params	-	массив параметров функции принадлежности входной переменной;
output	-	массив выходных переменных;
output.name	-	наименование выходной переменной;
output.range	-	диапазон изменения выходной переменной;
output.mf	-	массив функций принадлежности выходной переменной;
output.mf.name	-	наименование функции принадлежности выходной переменной;
output.mf.type	-	модель функции принадлежности выходной переменной. Запрограммированные модели для системы типа Мамдани: dsigmf - функция принадлежности в виде разности между двумя сигмоидными функциями; gauss2mf - двухсторонняя гауссовская функция принадлежности; gaussmf - гауссовская функция принадлежности; gbellmf - обобщенная колокообразная функция принадлежности; pimf - пи-подобная функция принадлежности; psigmf - произведение двух сигмоидных функций принадлежности. Запрограммированные модели для системы типа Сугэно: constatnt - константа (функция принадлежности в виде синглтона); linear - линейная комбинация входных переменных;
output.mf.params	-	массив параметров функции принадлежности выходной переменной;
rule	-	массив правил нечеткой базы знаний;
rule.antecedent	-	посылки правила. Указываются порядковые номера термов в порядке записи входных переменных. Число 0 указывает на то, что значение соответствующей входной переменной не влияет на истинность правила;
rule.consequent	-	заключения правила. Указываются порядковые номера термов в порядке записи выходных переменных. Число 0 указывает на то, что правило не распространяется на соответствующую выходную переменную;
rule.weight	-	вес правила. Задается числом из диапазона [0, 1];
rule.connection	-	логическая связка переменных внутри правила: 1 - логическое И; 2 - логическое ИЛИ.

Для доступа к свойствам системы нечеткого логического вывода достаточно указать имя соответствующего поля. Например, команда FIS_NAME.rule(1).weight=0.5устанавливает вес первого правила в 0.5, команда length(FIS_NAME.rule)определяет количество правил в базе знаний, а команда FIS_NAME.input(1).mf(1).name='низкий'переименовывает первый терм первой входной переменной в "низкий".

Структура fis-файла

Системы нечеткого логического вывода сохраняется на диске в виде fis-файлов - текстовых файлов специального формата. Функции readfis и writefis используются для чтения и записи этих файлов. Иногда удобно модифицировать системы нечеткого логического вывода путем редактирования их fis-файлов, без вызова GUI -модулей Fuzzy Logic Toolbox. Для изменения fis-файлов можно использовать любой текстовый редактор. Однако редактировать fis-файлы надо осторожно так как, изменения некоторых строчек файла влечет за собой необходимость корректирования нескольких других. Например, если при редактировании удален терм, используемый для лингвистической оценки входной или выходной переменной, то необходимо убедиться, что в базе знаний отсутствуют правила, включающие этой терм.

Формат fis-файла описан в табл. 5.1 на примере файла tipper .fis - демонстрационной системы нечеткого логического вывода, определяющей размер чаевых в ресторане. Обратим внимание, что правила базы знаний представлены в индексном формате.

Таблица 5.1 - Формат fis - файла (на примере файла tipper.fis)

Строки файла	Описание
% $ Revision: 1.1 $	строка комментария
[System]	указатель, на начало описания общих параметров системы нечеткого логического вывода
Name='tipper'	наименование системы
Type='mamdani'	тип системы нечеткого логического вывода
NumInputs=2	количество входных переменных системы
NumOutputs=1	количество выходных переменных системы
NumRules=3	количество правил в базе знаний
AndMethod='min'	реализация логической операции И
OrMethod='max'	реализация логической операции ИЛИ
ImpMethod='min'	реализация операции импликации
AggMethod='max'	реализация операции аггреатирования
DefuzzMethod='centroid'	метод дефаззификации
[Input1]	указатель, на начало описания первой входной переменной
Name='service'	наименование первой входной переменной
Range=[0 10]	диапазон изменения
NumMFs=3	количество термов
MF1='poor':'gaussmf',[1.5 0]	наименование первого терма, тип функции принадлежности и ее параметры
MF2='good':'gaussmf',[1.5 5]	наименование второго терма, тип функции принадлежности и ее параметры
MF3='excellent':'gaussmf',[1.5 10]	наименование второго терма, тип функции принадлежности и ее параметры
[Input2]	указатель, на начало описания второй входной переменной
Name='food'	наименование второй входной переменной
Range=[0 10]	диапазон изменения
NumMFs=2	количество термов
MF1='rancid':'trapmf',[0 0 1 3]	наименование первого терма, тип функции принадлежности и ее параметры
MF2='delicious':'trapmf',[7 9 10 10]	наименование второго терма, тип функции принадлежности и ее параметры
[Output1]	указатель, на начало описания первой выходной переменной
Name='tip'	наименование выходной переменной
Range=[0 30]	диапазон изменения
NumMFs=3	количество термов
MF1='cheap':'trimf',[0 5 10]	наименование первого терма, тип функции принадлежности и ее параметры
MF2='average':'trimf',[10 15 20]	наименование второго терма, тип функции принадлежности и ее параметры
MF3='generous':'trimf',[20 25 30]	наименование второго терма, тип функции принадлежности и ее параметры
[Rules]	указатель, на начало описания правил базы знаний
1 1, 1 (1) : 2 2 0, 2 (1) : 1 3 2, 3 (1) : 2	правила базы знаний в индексном формате

В оглавление книги \ К следующему разделу \ К предыдущему разделу

Fuzzy Logic Toolbox включает 11 встроенных функций принадлежностей, которые используют следующие основные функции:

• кусочно-линейную;
• гауссовское распределение;
• сигмоидную кривую;
• квадратическую и кубические кривые.

Для удобства имена всех встроенных функций принадлежности оканчиваютя на mf.Вызов функции принадлежности осуществляется следующим образом:

namemf(x, params),

гдеnamemf – наименование функции принадлежности;
x– вектор, для координат которого необходимо рассчитать значения функции принадлежности;
params– вектор параметров функции принадлежности.

Простейшие функции принадлежности треугольная (trimf) и трапециевидная (trapmf) формируется с использованием кусочно-линейной аппроксимации. Трапециевидная функция принадлежности является обобщение треугольной, она позволяет задавать ядро нечеткого множества в виде интервала. В случае трапециевидной функции принадлежности возможна следующая удобная интерпретация: ядро нечеткого множества – оптимистическая оценка; носитель нечеткого множества – пессимистическая оценка.

Две функции принадлежности – симметричная гауссовская (gaussmf) и двухстороняя гауссовская (gaussmf) формируется с использованием гауссовского распределения. Функция gaussmf позволяет задавать ассиметричные функция принадлежности. Обобщенная колоколообразная функция принадлежности (gbellmf) по своей форме похожа на гауссовские. Эти функции принадлежности часто используются в нечетких системах, так как на всей области определения они является гладкими и принимают ненулевые значения.

Функции принадлежности sigmf,dsigmf, psigmf основаны на использовании сигмоидной кривой. Эти функции позволяют формировать функции принадлежности, значения которых начиная с некоторого значения аргумента и до + (-) равны 1. Такие функции удобны для задания лингвистических термов типа “высокий” или “низкий”.

Полиномиальная аппроксимация применяется при формировании функций zmf, pimf и smf, графические изображения которых похожи на функции sigmf,dsigmf, psigmf, соответственно.

Основная информация о встроенных функциях принадлежности сведена в табл. 6.1. На рис. 6.1 приведены графические изображения функций принадлежности, полученные с помощью демонстрационной сценария mfdemo. Как видно из рисунка, встроенные функции принадлежности позволяют задавать разнообразные нечеткие множества.

В Fuzzy Logic Toolbox предусмотрена возможность для пользователя создания собственной функции принадлежности. Для этого необходимо создать m-функцию, содержащую два входных аргумента – вектор, для координат которого необходимо рассчитать значения функции принадлежности и вектор параметров функции принадлежности. Выходным аргументом функции должен быть вектор степеней принадлежности. Ниже приведена m-функция, реализующая колоколообразную функцию принадлежности :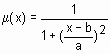

function mu=bellmf(x, params)
%bellmf – bell membership function;
%x – input vector;
%params(1) – concentration coefficient (>0);
%params(2) – coordinate of maximuma.
a=params(1);
b=params(2);
mu=1./(1+ ((x-b)/a).^2);

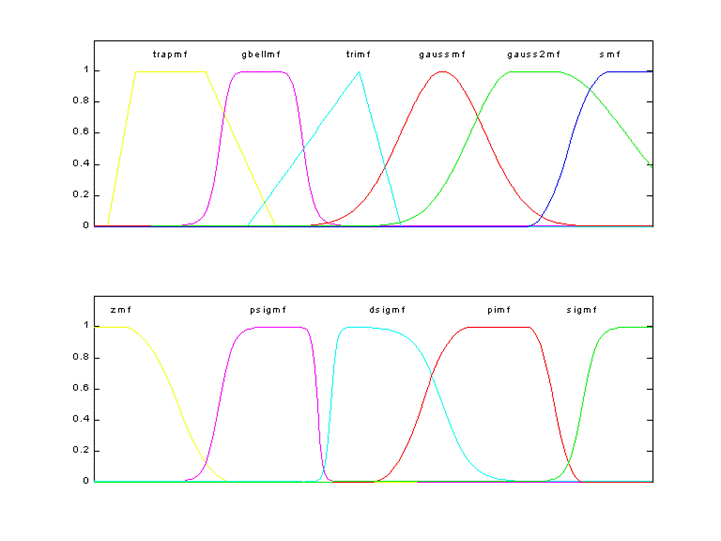
Рисунок 6.1. Встроенные функции принадлежности

Таблица 6.1. Функции принадлежности

Наименование функции	Описание	Аналитическая формула	Порядок параметров
dsigmf	функция принадлежности в виде разности между двумя сигмоидными функциями		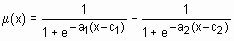[a1 c1 a2 c2]
gauss2mf	двухсторонняя гауссовская функция принадлежности	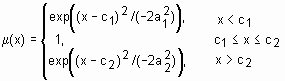если c1<c2, то ; если c1>c2, то 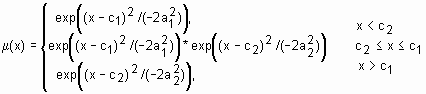.	[a1 c1 a2 c2]
gaussmf	симметричная гауссовская функция принадлежности		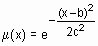[c b]
gbellmf	обобщенная колокообразная функция принадлежности		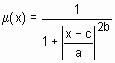[a b c]
pimf	пи-подобная функция принадлежности	произведение smf и zmf функций	[a b c d] [a d] – носитель нечеткого множества; [b c] – ядро нечеткого множества;
psigmf	произведение двух сигмоидных функций принадлежности		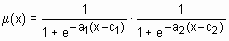[a1 c1 a2 c2]
sigmf	сигмоидная функция принадлежности		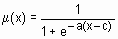[a c]
smf	s-подобная функция принадлежности		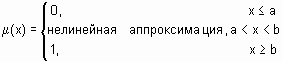[a, b]
trapmf	трапециевидная функция принадлежности		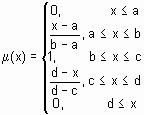[a, b, c, d]
trimf	треугольная функция принадлежности		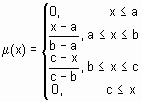[a, b, c]
zmf	z-подобная функция принадлежности		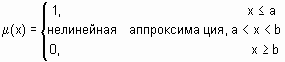[a, b]

FIS-редактор

FIS-редактор предназначен для создания, сохранения, загрузки и вывода на печать систем нечеткого логического вывода, а также для редактирования следующих свойств:

• тип системы;
• наименование системы;
• количество входных и выходных переменных;
• наименование входных и выходных переменных;
• параметры нечеткого логического вывода.

Загрузка FIS-редактора происходит с помощью команды fuzzy.В результате появляется интерактивное графическое окно, приведенное на рис. 3.2. На этом же рисунке также указаны функциональные назначения основных полей графичекого окна. В нижней части графического окна FIS-редактора расположены кнопки Helpи Close, которые позволяют вызвать окно справки и закрыть редактор, соответственно.

FIS-редактор содержит 8 меню. Это три общесистемных меню - File, Edit, View, и пятьменю для выбора параметров нечеткого логического вывода – And Method,Or Method,Implication,AggregationиDefuzzification.

Меню File

Это общее меню для всех GUI-модулей используемых с системами нечеткого логического вывода. Общий вид меню показан на рис. 7.1.

Рисунок 7.1 – Меню File

С помощью команды New FIS…пользователь имеет возможность создать новую систему нечеткого логического вывода. При выборе этой команды появятся две альтернативы: Mamdaniи Sugeno, которые определяют тип создаваемой системы. Создать систему типа Mamdani можно также нажатием Ctrl+N.

С помощью команды Importпользователь имеет возможность загрузить ранее созданную систему нечеткого логического вывода. При выборе этой команды появятся две альтернативы From Workspace…иFrom disk, которые позволяют загрузить систему нечеткого логического вывода из рабочей области MatLabи с диска, соответственно. При выборе команды From Workspace…появится диалоговое окно, в котором необходимо указать идентификатор системы нечеткого логического вывода, находящейся в рабочей области MatLab. При выборе команды From disk появится диалоговое окно (рис. 7.2), в котором необходимо указать имя файла системы нечеткого логического вывода. Файлы систем нечеткого логического вывода имеют расширение .fis. Загрузить систему нечеткого логического вывода с диска можно также нажатием Ctrl+Nили командой

fuzzy FIS_name,

где FIS_name – имя файла системы нечеткого логического вывода.

Рисунок 7.2 – Окно загрузки системы нечеткого логического вывода с диска

При выборе команды Export появятся две альтернативы To Workspace…иTo disk, которые позволяют скопировать систему нечеткого логического вывода в рабочую область MatLabи на диск, соответственно. При выборе команды To Workspace…появится диалоговое окно, в котором необходимо указать идентификатор системы нечеткого логического вывода, под которым она будет сохранена в рабочей области MatLab. При выборе команды To disk появится диалоговое окно, в котором необходимо указать имя файла системы нечеткого логического вывода. Скопировать систему нечеткого логического вывода в рабочую область и на диск можно также нажатием Ctrl+TиCtrl+S, соответственно.

Команда Printпозволяет вывести на принтер копию графического окна. Печать возможна также по нажатию Ctrl+P.

Команда Closeзакрывает графическое окно. Закрытия графического окна происходит по нажатию Ctrl+Wили однократного щелчка левой кнопки мыши по кнопке Close.

Меню Edit

Общий вид меню приведен на рис. 7.3.

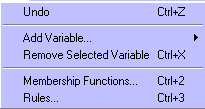
Рисунок 7.3 – Меню Edit

Команда Undoотменяет ранее совершенное действие. Выполняется также по нажатию Ctrl+Z.

Команда Add Variable…позволяет добавить в систему нечеткого логического вывода еще одну переменную. При выборе этой команды появятся две альтернативы InputиOutput, которые позволяют добавить входную и выходную переменную, соответственно.

Команда Remove Selected Variableудаляеттекущую переменную из системы. Признаком текущей переменной является красная окантовка ее прямоугольника. Назначение текущей переменной происходит с помощью однократного щелчка левой кнопки мыши по ее прямоугольнику. Удалить текущую переменную можно также с помощью нажатия Ctrl+X.

Команда Membership Function…открывает редактор функций принадлежностей. Эта команда может быть также выполнена нажатием Ctrl+2.

Команда Rules…открывает редактор базы знаний. Эта команда может быть также выполнена нажатием Ctrl+3.

Меню View

Это общее меню для всех GUI-модулей, используемых с системами нечеткого логического вывода. Общий вид меню показан на рис. 7.4. Это меню позволяет открыть окно визуализауии нечеткого логического вывода (команда Rulesили нажатие клавиш Ctrl+5) и окно вывода поверхности “входы-выход”, соответствующей системе нечеткого логического вывода (команда Surfaceили нажатие клавиш Ctrl+6).

Рисунок 7.4 – Меню View

Меню And Method

Это меню позволяет установить следующие реализации логической операции И:

• min –минимум;
• prod –умножение.

Пользователь также имеет возможность установить собственную реализацию операции И. Для этого необходимо выбрать команду Custom…и в появившемся графическом окне напечатать имя функции, реализующей эту операцию.

Меню Or Method

Это меню позволяет установить следующие реализации логической операции ИЛИ:

• max– умножение;
• probor -вероятностное ИЛИ.

Пользователь также имеет возможность установить собственную реализацию операции ИЛИ. Для этого необходимо выбрать команду Custom…и в появившемся графическом окне напечатать имя функции, реализующей эту операцию.

Меню Implication

Это меню позволяет установить следующие реализации импликации:

• min – минимум;
• prod– умножение.

Пользователь также имеет возможность установить собственную реализацию импликации. Для этого необходимо выбрать команду Custom…и в появившемся графическом окне напечатать имя функции, реализующей эту операцию.

Меню Aggregation

Это меню позволяет установить следующие реализации операции объединения функций принадлежности выходной переменной:

• max– максимум;
• sum– сумма;
• probor -вероятностное ИЛИ.

Пользователь также имеет возможность установить собственную реализацию этой операции. Для этого необходимо выбрать команду Custom…и в появившемся графическом окне напечатать имя функции, реализующей эту операцию

Меню Defuzzification

Это меню позволяет выбрать метод дефаззификации. Для систем типа Мамдани запрограммированы следующие методы:

• centroid – центр тяжести;
• bisector –медиана;
• lom – наибольший из максимумов;
• som – наименьший из максимумов;
• mom – среднее из максимумов.

Для систем типа Сугэно запрограммированы следующие методы:

• wtaver – взвешенное среднее;
• wtsum – взвешенная сумма.

Пользователь также имеет возможность установить собственный метод деффазификации. Для этого необходимо выбрать команду Custom…и в появившемся графическом окне напечатать имя функции, реализующей эту операцию.