Дескриптивне висловлювання 6 страница

3. Солодухин О.А. Логика: Для студентов вуза: [Частина книги: Глава 4. Рассуждение]. – Ростов-н/Д: Феникс, 2004. – С. 128-135.

Додаткова:

1. Войшвилло Е.К., Дегтярев М.Г. Логика: Учеб. для студ. высш. учеб. заведений: [Частина книги: §36. Непосредственные умозаключения]. – М.: ВЛАДОС-ПРЕСС, 2001. – С. 349-362. – Режим доступу: http://khartn.name/ru/isearch/download/11079

2. Новоселов М.М. Логика абстракций (методологический анализ). Ч. 1. Глава 1. Абстракия и логика обоснования. – М.: ИФ РАН, 2000. – С. 8-57.

3. Тягло А.В. Критическое мышление на основе элементарной логики: учебное пособие. – Харьков: ХНУ им. В. Н. Каразина, 2001. – 210 с.

1 Словник-мінімум

Безпосередні умовиводи через трансформацію суджень – міркування, в яких висновок робиться з одного засновку, їх можна отримати завдяки операціям перетворення суджень або обернення суджень.

Обернення (конверсія) – логічна операція над судженнями, що полягає у перестановці місцями суб’єкта і предиката.

Перетворення (обверсія) – логічна операція над судженнями, яка полягає у зміні його якості на протилежну. Її можливість ґрунтується на тому, що подвійне заперечення дає ствердження.

Протиставлення суб’єкту – трансформація суджень, коли над судженням спочатку роблять операцію обернення, а потім операцію перетворення.

Протиставлення предикату – трансформація суджень, коли над судженням спочатку роблять операцію перетворення, а потім операцію обернення.

Тема № 2

ЗАГАЛЬНА ХАРАКТЕРИСТИКА ПРОСТОГО КАТЕГОРИЧНОГО СИЛОГІЗМУ

План

1. Визначення та структура простого категоричного силогізму.

2. Загальні правила простого категоричного силогізму.

3. Аксіома простого категоричного силогізму.

& Методичні вказівки

«Винахід силогістичної форми є одним з найпрекрасніших і навіть найважливіших відкриттів людського духу» (Г.В. Ляйбніц).

Простий категоричний силогізм (ПКС) – це вид дедуктивного умовиводу, що складається з двох засновків і висновку, які є категоричними судженнями.

Приклад:

Усі ссавці (М) дихають легенями (Р) – більший засновок

Усі кити (S) – ссавці (М) – менший засновок

Усі кити (S) дихають легенями (Р) – висновок

Поняття, що входять до складу силогізму, називаються термінами силогізму. Меншим терміном називається суб’єкт висновку і позначається S. У нашому прикладі менший термін – кити. Засновок, який містить у собі менший термін, називається меншим засновком. Більшим терміном називається предикат висновку і позначається як Р. У нашому випадку – дихають легенями (S і Р називаються ще крайніми термінами). Засновок, який містить у собі більший термін, називається більшим засновком. Середнім терміном називається термін, якого немає у висновку, але який є в обох засновках, що забезпечує логічний зв’язок між засновками. Позначається як М – ссавці.

Правила силогізму поділяються на загальні та правила фігур (спеціальні). Загальні правила силогізму застосовані до усіх простих силогізмів, незалежно від того, за якою фігурою вони побудовані. Спеціальні правила діють тільки для кожної фігури силогізму і тому часто називаються правилами фігур. Загальних правил категоричного силогізму існує всього сім: три з них – це правила термінів, чотири – правила засновків.

Загальні правила силогізму

1. У силогізмі повинно бути лише три терміни. Приклад:

Рух вічний.

Ходіння до університету – рух.

=> Ходіння до університету вічне.

Обидва засновки цього силогізму є істинними судженнями, проте з них випливає помилковий висновок, тому що порушено дане правило. Слово рух вживається у двох засновках у двох різних значеннях: рух як філософська категорія і рух як фізична дія. Тому, термінів у силогізмі три: рух, ходіння до університету, вічність; а значень (оскільки один з термінів вживається у двох різних значеннях) чотири, тобто зайве значення має на увазі зайвий термін. У наведеному прикладі силогізму було не три, а чотири (за значенням) терміни. Помилка, що виникає при порушенні наведеного вище правила, називається почетверінням термінів.

2. Середній термін має бути розподілений хоч б в одному із засновків. Повне коло (за схемою Ейлера) означатиме розподілений термін (+), а неповне – нерозподілений (-). Приклад:

Усі кішки (К) – це живі істоти (ж. і). Сократ (С) – це теж жива істота. => Сократ – це кішка.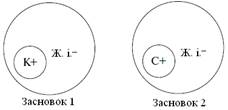

З двох істинних засновків отримуємо помилковий висновок. Зображуємо колами Ейлера відношення між термінами у засновках силогізму і встановлюємо розподіленість цих термінів.

Середній термін (живі істоти) у даному випадку нерозподілений у жодному із засновків, а за правилом він має бути розподілений хоч б в одному. Помилка, що виникає при порушенні даного правила, так і називається – нерозподіленість середнього терміну у кожному засновку.

3. Термін, який був нерозподілений у засновку, не може бути розподілений у висновку. Приклад:

Усі яблука (Я) – їстівні предмети (Ї. п.). Усі груші (Г) – це не яблука. => Усі груші – неїстівні предмети.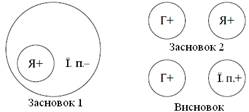

Засновки силогізму є істинними судженнями, а висновок – заперечний. Зображуємо колами Ейлера відношення між термінами у засновках і у висновку силогізму та встановлюємо розподільність цих термінів.

У даному випадку предикат висновку, або більший термін силогізму (їстівні предмети),у першому засновку є нерозподіленим (-), а у висновку – розподіленим (+), що забороняється даним правилом. Помилка, що виникає при його порушенні, називається розширенням більшого терміну.

4. У силогізмі не повинно бути двох заперечних засновків. Хоч б один із них має бути стверджувальним (можуть бути стверджувальними і обидва засновки). Якщо два засновки у силогізмі заперечні, то висновок з них або взагалі зробити не можна, або ж, якщо його зробити можливо, він буде помилковим або, принаймні, недостовірним, імовірним. Приклад:

Снайпери не можуть мати поганого зору.

Усі мої друзі – не снайпери.

=> Усі мої друзі мають поганий зір.

Обидва засновки у силогізмі є заперечними судженнями, і, незважаючи на їх істинність, з них отримуємо помилковий висновок. Помилка, яка виникає у даному випадку, так і називається – два заперечних засновки.

5. У силогізмі не повинно бути двох часткових засновків.

Хоч б один із засновків має бути загальним (можуть бути загальними і обидва засновки). Якщо два засновки у силогізмі є частковими судженнями, то висновок з них зробити неможливо. Приклад:

Деякі філософи – матеріалісти.

Деякі філософи – ідеалісти.

=>?

З цих засновків ніякого висновку отримати неможливо, тому що обидва вони є частковими. Помилка, що виникає при порушенні цього правила, так і називається – два часткових засновки.

6. Якщо один із засновків заперечний, то і висновок має бути заперечним.

Приклад:

Усі травоядні живляться рослинною їжею.

Усі тигри не живляться рослинною їжею.

=> Усі тигри не є травоядними.

З двох засновків цього силогізму не можна отримати стверджувальний висновок. Він може бути виключно заперечним.

7. Якщо один із засновків частковий, то і висновок має бути частковим.

Приклад:

Усі олімпійські чемпіони є спортсменами.

Деякі українці – це олімпійські чемпіони.

=> Деякі українці – це спортсмени.

У цьому силогізмі з двох засновків неможливо отримати загальний висновок. Він може бути лише частковим, оскільки другий засновок є частковим.

Аксіома силогізму є віддзеркаленням багатовікової практики людей, мільярдного повторення однієї й тієї ж розумової конструкції. Залежно від того, розглядаються засновки у кількісному або якісному (об’ємному чи змістовному) сенсі, розрізняют два її формулювання:

1) Dictum de omni et de nullo (сказане про усе і ні про одне): усе, що стверджується або заперечується про клас предметів у цілому, стверджується або заперечується і про частину або окремий елемент цього класу;

2) Nota notae est nota rei (ознака ознаки речі є ознакою самої речі).

Аксіома силогізму є вихідною логічною основою, на якій ґрунтується вся силогістика.

? Завдання для самоконтролю

1. Встановіть правильність силогізмів, наведених нижче, за допомогою графічної схеми відношень між їх термінами:

1.1. Усі стародавні математики були філософами. Піфагор – давньогрецький математик. Піфагор – філософ.

1.2. Деякі студенти старанні. Серед старанних учнів є відмінники. Деякі студенти – відмінники.

1.3. Деякі підручники мають схеми і графіки. Жодна книга, що має схеми і графіки, мені не цікава. Деякі підручники мені не цікаві.

1.4. Будь-яка думка має свою форму. Будь-яка форма має зміст. Будь-яка думка має зміст.

1.5. Геракліт був діалектиком. Усі діалектики говорять про те, що світ змінюється. Геракліт був серед тих, хто говорив, що світ змінюється.

1.6. «Люди, яким завжди ніколи, звичайно нічого не роблять» (Г. Ліхтенберг). Керівникові нашого відділу завжди ніколи. Керівник нашого відділу нічого не робить.

1.7. «Мистецтво є одним із засобів єднання людей» (Л.М. Толстой). Музика – вид мистецтва. Музика – засіб єднання людей.

1.8. «Нерозсудлива людина здатна захопитися будь-яким вченням» (Геракліт). Ця людина – цілком розумна. Ця людина не здатна захопитися будь-яким вченням.

2. Перевірте правильність наступних силогізмів. Які із загальних правил силогізму порушені при їх побудові:

2.1. Усі міста – населені пункти. Село не є містом. Отже, село не є населеним пунктом.

2.2. Деякі автомашини деренчать на ходу. Моя автомашина – це деяка автомашина. Тому недивно, що моя автомашина деренчить на ходу.

2.3. Жодна робота, в якій немає нових ідей, не може бути премійована. Робота Пробийголови не премійована. Отже, в ній немає нових ідей.

2.4. Деякі люди мають здатність до швидкого і точного розрахунку. Деякі люди – математики. Отже, усі математики мають здатність до швидкого і точного розрахунку.

Література

Основна:

1. Каратини Р. Введение в философию: [Частина книги: Часть 1 Логика и эпистемология. I. Логика]. – М.: Изд-во Эксмо, 2003. – С. 447-478.

2. Кириллов В.И., Старченко А.А. – Логика: [Частина книги: Глава VII. Дедуктивные умозаключения. Выводы из простых суждений. § 3. Простой категорический силлогизм] / Изд. 6-е, перераб. и доп. – М.: ТК Велби, Изд-во Проспект, 2008. – С. 111-123.

3. Коэн М., Нагель Э. Введение в логику и научный метод: [Частина книги: Книга І. Формальная логика. Глава IV. Категорический силлогизм] / Пер. с англ. П.С. Куслия. – Челябинск, Пермь: Социум, 2010. – С. 124-149.

Додаткова:

1. Войшвилло Е.К., Дегтярев М.Г. Логика: Учеб. для студ. высш. учеб. заведений: [Частина книги: § 37. Простой категорический силлогизм]. – М.: ВЛАДОС-ПРЕСС, 2001. – С. 363-377. – Режим доступу: http://khartn.name/ru/isearch/download/11079

2. Зиновьев А.А. Логика высказываний и теория вывода / Вст. статья В.А. Лекторского. – М.: Изд-во ЛКИ, 2010. – 160 с.

1 Словник-мінімум

Більший засновок ПКС– засновок, що містить більший термін ПКС.

Більший термін ПКС – предикат висновку ПКС.

Меншим засновкомПКС є той його засновок, що містить менший термін.

Менший термін ПКС– суб’єкт висновку ПКС.

Простий категоричний силогізм (ПКС) – різновид дедуктивних умовиводів, що являє собою систему трьох взаємопов’язаних суджень виду: А (Всі S є P), Е (Всі S не є P), І (Деякі S є P), О (Деякі S не є P). Перші два судження є засновками ПКС, а третє – висновком.

Терміни ПКС – суб’єкти і предикати засновків і висновку умовиводу.

Середній термін ПКС– це термін, який входить лише у засновки й якого немає у висновку ПКС.

Тема № 3

ФІГУРИ ТА МОДУСИ ПРОСТОГО КАТЕГОРИЧНОГО СИЛОГІЗМУ

План

1. Схеми фігур простого категоричного силогізму.

2. Розподіленість термінів у фігурах простого категоричного силогізму.

3. Правила фігур простого категоричного силогізму.

4. Модуси простого категоричного силогізму.

& Методичні вказівки

Три терміни силогізму можуть бути розташовані у ньому різним чином. Залежно від місця середнього терміну розрізняють чотири фігури простого категоричного силогізму.

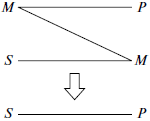
Першою називають таку фігуру силогізму, в якій середній термін займає місце суб’єкта в більшому засновку і місце предиката – в меншому.

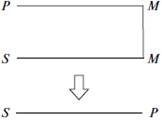
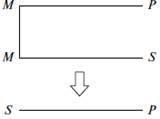
Другою називають таку фігуру силогізму, в якій середній термін займає місце предиката в обох засновках.

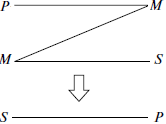
Третьою називають таку фігуру, в якій середній термін займає місце суб’єкта в обох засновках.

Четвертою називають таку фігуру силогізму, в якій середній термін займає місце предиката в більшому засновку і суб’єкта – в меншому.

Схеми фігур ПКС

І фігура	ІІ фігура	ІІІ фігура	ІV фігура

Приклади та розподіленість термінів у фігурах ПКС

І ф і г у р а	Усі поети (М) – це творчі люди (Р). Вася (S) – поет (М). => Вася (S) – це творча людина (Р).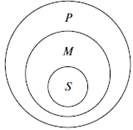
ІІ ф і г у р а	Усі риби (Р) дихають зябрами (М). Усі кити (S) не дихають зябрами (М). => Усі кити (S) не риби (Р).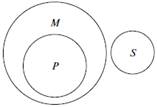
ІІІ ф і г у р а	Усі тигри (М) – це ссавці (Р). Усі тигри (М) – це хижаки (S). => Деякі хижаки (S) – ссавці (Р).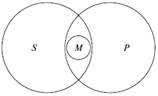
ІV ф і г у р а	Усі квадрати (Р) – це прямокутники (М). Усі прямокутники (М) – це не трикутники (S). => Усі трикутники (S) – це не квадрати (Р).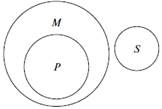

Розподіленість термінів у засновках та висновку ПКС може бути іншою, залежно від обсягів термінів, що входять до їх складу.

Кожна з фігур ПКС має свої спеціальні правила:

І фігура.Більший засновок має бути загальним, менший – стверджувальним.

ІІ фігура.Більший засновок має бути загальним та один із засновків має бути заперечним. Висновок теж є заперечним судженням.

ІІІ фігура.Менший засновок має бути стверджувальним, а висновок – частковим.

ІV фігура.Якщо більший засновок є стверджувальним судженням, то менший засновок – судження загальне. Якщо один із засновків є заперечним судженням, то більший засновок – судження загальне. Якщо менший засновок є судженням стверджувальним, то висновок – частковим судженням.

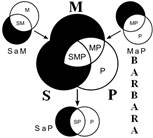
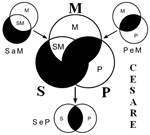
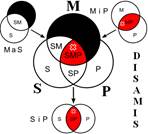
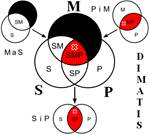
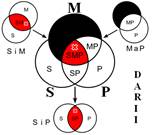
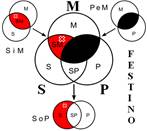
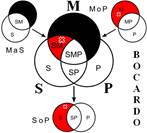
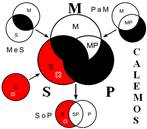
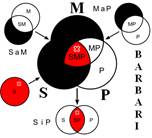
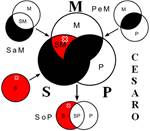
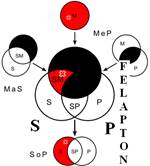
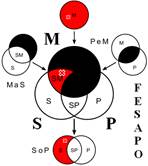
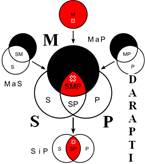
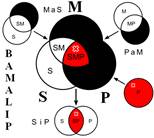
Розподіленість термінів у модусах фігур простого категоричного силогізму

№	І фігура	ІІ фігура	ІІІ фігура	ІV фігура

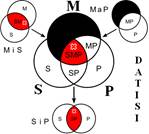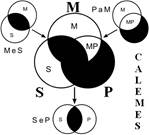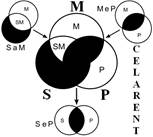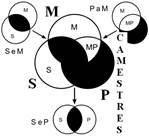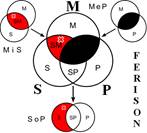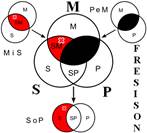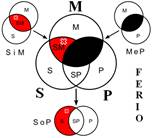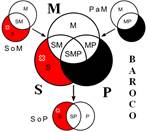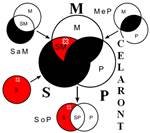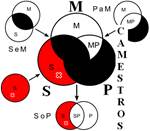Кожне з простих суджень, з яких складається простий силогізм, належить до одного з чотирьох видів (А, I, Е, О). Набір простих суджень, що входять до складу силогізму, називається модусом (видом) простого силогізму. Приклад:

Усі журнали – це періодичні видання.

Усі книги не є періодичними виданнями.

=> Усі книги не є журналами.

У цьому силогізмі перший засновок є простим судженням виду Е (загальнозаперечне судження), другий засновок – це просте судження виду А (загальностверджувальне судження),висновок є простим судженням виду Е (загальнозаперечне судження). Тому розглянутий силогізм має модус ЕAЕ, або cesare. Останнє латинське слово нічого не означає і ніяк не перекладається – це просто поєднання літер, підібране так, щоб у ньому були присутніми три літери, що символізують модус силогізму ЕAЕ.

Всього модусів в усіх чотирьох фігурах (тобто можливих комбінацій простих суджень у силогізмі) – 256. У кожній фігурі 64 модуси. Проте з цих модусів тільки 19 сильних (які дають достовірні висновки) та 5 слабких (правдоподібних), які послаблюють сильні модуси, що відображено у таблиці, наведеній вище. Наше завдання – уміти визначати фігуру і модус будь-якого простого силогізму.

І фігура застосовується у міркуваннях частіше, ніж всі інші разом. Модуси ІІ фігури слугують, як правило, для спростування певних положень. ІІІ фігура застосовується для показу винятків із правил. ІV фігура майже не використовується.

? Завдання для самоконтролю

1. Обґрунтуйте, чому модус ААА I фігури є правильним.

2. Обґрунтуйте, чому модус ААА II фігури не є правильним.

3. Проаналізуйте логічну структуру наступних простих категоричних силогізмів – знайдіть висновки, встановіть терміни (менші, більші і середні), великі і менші засновки, визначте їх фігури.

3.1. Деякі метали не тонуть у воді, оскільки натрій – метал, а натрій не тоне у воді.

3.2. Деякі бджолярі не є хіміками, оскільки деякі бджолярі – художники, а жоден хімік не є художником.

4. Які з правил фігур простого категоричного силогізму порушені у наступних випадках:

4.1. Будь-який правильний силогізм має три терміни. Цей силогізм має три терміни. Отже, цей силогізм правильний.

4.2. Деякі елементарні частки мають негативний заряд. Деякі елементарні частки – електрони. Отже, усі електрони мають негативний заряд.

5. Встановіть фігуру і модус кожного силогізму, наведеного нижче, на підставі цього визначте, чи є вони правильними:

5.1. Б. Рассел – відомий логік. Б. Рассел – відомий філософ. Серед відомих філософів є відомі логіки.

5.2. Будь-яка брехня – умисне спотворення істини. Наклеп – умисне спотворення істини. Наклеп – це брехня.

5.3. Усі люди народжені вільними. Я – людина. Я народжений вільним.

Література

Основна:

1. Богдановський І.В. Логіка: Опорний конспект лекцій: [Частина книги: Розділ 2. Логічна характеристика форм мислення. Тема 6. Умовивід] / І.В. Богдановський, О.Г. Льовкіна. – К.: МАУП, 2004. – С. 61-84.

2. Каратини Р. Введение в философию: [Частина книги: Часть 1 Логика и эпистемология. I. Логика]. – М.: Изд-во Эксмо, 2003. – С. 447-478.

3. Конверський А.Є. Логіка (традиційна та сучасна): Підручник для студентів вищих навчальних закладів: [Частина книги: Книга перша. Традиційна логіка. Розділ Х. Умовивід]. – К.: Центр учбової літератури, 2008. – С. 215-282.

Додаткова:

1. Коэн М., Нагель Э. Введение в логику и научный метод / Моррис Коэн, Эрнест Нагель. Пер. с англ. П.С. Куслия. – Челябинск, Пермь: Социум, 2010. – 655 с. – Режим доступу: http://coollib.net/b/231744

2. Оккам У. Логика / Уильям Оккам. Избранное:Пер. с лат. А.В. Апполонова и М.А. Гарнцева под общ. ред. А.В. Апполонова. – М.: Едиториал УРСС, 2002. – С. 2-67.

3. Пхиденко С. Логіка і теологія за Середньовіччя // Людина і світ. – К. – 2004. – № 4 – С. 55-61.

1 Словник-мінімум

Модуси ПКС – такі їх схеми, в яких фіксується не лише їх фігура, а й конкретний вид (А, Е, І або О) засновків і висновків.

Сильні (правильні) модуси по кожній фігурі:

І фігура: ААА, ЕАЕ, АІІ, ЕІО.

ІІ фігура: ЕАЕ, АЕЕ, ЕІО, АОО.

ІІІ фігура: АІІ, ІАІ, ЕІО, ОАО, ЕАО, ААІ.

ІV фігура: АЕЕ, ІАІ, ЕІО, ЕАО, ААІ.

Фігури ПКС – різновиди ПКС, які відрізняються між собою залежно від розташування середнього терміна. Всього їх чотири.

Тема № 4

ЕНТИМЕМА

План

1. Види ентимем.

2. Етапи перевірки скорочених силогізмів.

3. Значення та застосування ентимем.

& Методичні вказівки

Простий категоричний силогізм називається повним, якщо він виражений розгорнуто, тобто у ньому є більший і менший засновки, а також висновок. У практиці мислення простий категоричний силогізм майже завжди застосовується у скороченій формі і називається ентимемою.

Сутність цієї назви (з грец. – «у думці») полягає у тому, що певна частина силогізму не виражається явно, а як би вимовляється у думці.

У дискусіях і суперечках, коли співрозмовник виражає свою думку у вигляді скороченого силогізму, необхідно завжди точно усвідомлювати, яке саме судження не виражене, а тільки мається на увазі у цьому міркуванні. Інакше неможливо повністю зрозуміти це міркування і спростувати, якщо воно неправильне. Нерідко люди виходять у своїх міркуваннях з помилкових або сумнівних положень, але не виражають їх явно, користуючись скороченими формами міркувань. Щоб знайти помилку у такому міркуванні і спростувати її, потрібно встановити те, що у ньому передбачається, але не виражається явно.

Розрізняють три види ентимем:

1) силогізм з пропущеним більшим засновком. Приклад: «Гуссерль – феноменолог. Отже, він філософ». Тут пропущений, але мається на увазі більший засновок: «Усі феноменологи – філософи»;

2) силогізм з пропущеним меншим засновком. Приклад: «Усі феноменологи – філософи. Отже, Гуссерль – філософ». Передбачається, що «Гуссерль – феноменолог»;

3) силогізм з пропущеним висновком. Приклад: «Усі феноменологи – філософи. Гуссерль – феноменолог». Передбачається, що «отже, він – філософ».

Значення ентимем полягає у тому, що за допомогою них досягається стислість думки, яка спонукає до міркувань того, до кого вона звернена.

Перевірка скороченого силогізму (ентимеми) починається із з’ясування питання: що в ній пропущено – засновок або висновок. Потім вона відновлюється, якщо це можливо, у повний правильний силогізм. Якщо в ентимемі був пропущений засновок, то ентимема вважається коректною, якщо вона не лише формально може бути відновлена у правильний силогізм, але і пропущений засновок змістовно істинний. Ентимема з пропущеним висновком коректна, якщо вона просто відновлюється у правильний силогізм.

Етапи відновлення (перевірки) ентимем

Треба перевірити скорочений силогізм: «Цю помилку мені важко виявити, оскільки я не знаю правил».

1 етап. Визначаємо, що пропущено – засновок або висновок – і записуємо у стандартній формі: висновок – під рискою, засновки над рискою. На наявність висновку в ентимемі вказують зазвичай слова: 1) «оскільки», «тому що» і тому подібні або 2) «означає», «тому», «таким чином». Слова першої групи вказують, що висновок стоїть перед ними, а після них йде пояснення до нього, тобто засновок, слова другої групи показують, що висновок йде після них. Якщо ж ніяких подібних слів немає, то в ентимемі пропущений висновок. У даній ентимемі висновок: «Я насилу виявлю цю помилку». Записуємо його під рискою, а засновок: «Я не знаю правил» – над рискою.

Я не знаю правил.

Я насилу виявлю цю помилку.

Далі для ентимем з пропущеним засновком:

2 етап. Знаходимо крайні терміни силогізму у висновку і в одному із засновків:

Я (S) не знаю правил (M).

Я (S) насилу виявлю цю помилку (Р).

3 етап. Визначаємо вид суджень – висновку і засновку – і розподіленість термінів у них. Висновок – стверджувальний, значить, і засновок слід розглядати як стверджувальне судження (інакше ентимема не відновиться). Якщо він стверджувальний, то його предикат, середній термін силогізму – «не знаю правил».

Усі S⁺ суть М^-

Усі S⁺ суть Р^-

4 етап. Визначаємо, які терміни входять до складу відновленого засновку, його якість, порядок термінів у ньому, щоб були дотримані правила розподіленості середнього і крайніх термінів. У нього входить більший і середній терміни, він стверджувальний, оскільки висновок стверджувальний, середній термін у ньому має бути розподіленим, оскільки він нерозподілений у наявному засновку, а більший термін може бути нерозподіленим (він нерозподілений у висновку).

Усі М⁺ суть Р^-

Усі S⁺ суть М^-

Усі S⁺ суть Р^-

5 етап. Змістовно формулюємо відновлений засновок і оцінюємо, чи є він істинним: «Усі, хто не знають правил, насилу виявлять цю помилку».

Істинність його залежатиме від того, про яку помилку і знання яких правил йдеться. Якщо ми визнаємо відновлений засновок істинним, то ентимема коректна, якщо помилковим, то некоректна.

Особливістю багатьох ентимем є здатність робити малопомітними формальні або змістовні недоліки, які стають, як правило, наявними у результаті відновлення ентимеми до повного силогізму. Тому оволодіння процедурою відновлення має важливе практичне значення.

Труднощі відновлення силогізмів за ентимемою можуть бути пов’язані з тим, що для правильного визначення понять (термінів), з яких формулюватиметься пропущений елемент (засновок або висновок), обов’язково треба знати логічні форми наявних елементів (двох засновків або засновку та висновку). Проте в реальних міркуваннях стандартні логічні форми категоричних суджень (з яких і складаються силогізми) використовуються далеко не завжди. Перш ніж приводити судження до стандартної форми, треба розібратися у їхньому сенсі, що може виявитися непростою справою.