Аксиомы логики высказываний

Логика первого порядка. Аксиомы булевой алгебры и логики высказываний.

Предика́т(лат. praedicatum – заявленное, упомянутое,сказанное) – любое математическое высказывание, в котором есть, по меньшей мере, одна переменная, n-арная логическая формула P(X) P: X→ {ИСТИНА, ЛОЖЬ}.

· Предикат является способом записи (формализации) высказываний

· Предикат является основным объектом изучения логики первого порядка

· Исчисление предикатов производится в рамках формальной грамматики логики первого порядка, корнями уходящей в булеву алгебруи логику высказываний

· Предикат называют тождественно-истинным и пишут:

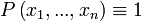
если на любом наборе аргументов он принимает значение 1.

· Предикат называют тождественно-ложным и пишут:

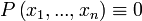
если на любом наборе аргументов он принимает значение 0.

· Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение. Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. Д

Логика первого порядка

Логика первого порядка (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка.

Словарь

М = < Т, Р, А, F >

Словарь логики первого порядка состоит из

s Кванторов: существования $ и всеобщности "

s Логических операторов:

§ Ù конъюнкция (пересечение, логическое «И»)

§ Ú дизъюнкция (объединение, логическое «ИЛИ»)

§ Ø отрицание (также обозначается верхней чертой)

§ → импликация

s Служебных символов: скобки и запятые

s 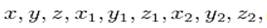Переменных:

s Констант: 1, T – ИСТИНА; 0, ^ – ЛОЖЬ

s Равенств: = (обычное) и º (тождественное)

s Связки

§ Ù конъюнкция

§ Ú дизъюнкция

§ → импликация

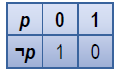
§ Ø отрицание

Синтаксис

М = < Т, Р, А, F >

Синтаксис логики первого порядка состоит из

s Термов

§ Переменная

§ Функция: выражение f(x₁, x₂,…, x_n) является n-арной функцией

s Формул

§ Предикаты: если P является символом n-арного предиката и t₁, t₂,…,

t_n– термы, то P(t₁, t₂,…, t_n) – формула

§ Равенств: для термов t₁ и t₂, t₁ = t₂ – формула

§ Отрицаний: для формулы j,Øj – формула

§ Бинарных операторов: для формул j и y,j→y – формула

§ Кванторов: для формулы j и переменной X, $Xj и "Xj – формулы

Старшинство операторов

Приоритеты (старшинство) логических операторов и

кванторов определяется в следующем порядке:

1. Скобки ( )

2. Кванторы существования $ и всеобщности ", оператор

отрицания Ø

3. Конъюнкция Ù

4. Дизъюнкция Ú

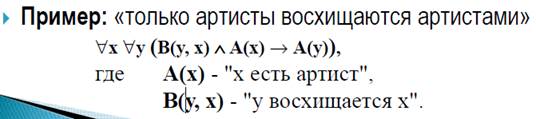5. Импликация →

Аксиомы

М = < Т, Р, А, F >

Аксиомы булевой алгебры

Аксиомы логики высказываний

Логика высказываний (или пропозициональная логика от англ. propositional logic) — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, её можно охарактеризовать как классическую логику нулевого порядка. Логика высказываний является простейшей логикой, максимально близкой к человеческой логике неформальных рассуждений и известна ещё со времён античности.

Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний

Аксиомы логики предикатов

Система логических аксиом логики первого порядка состоит из аксиом исчисления высказываний дополненной двумя новыми аксиомами:

§ ,

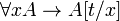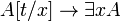§ , где 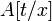— формула, полученная в результате подстановки терма 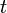вместо каждой свободной переменной 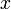, встречающейся в формуле .

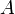Правил вывода 2:

• Modus ponens:
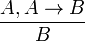
• Правило обобщения (англ.):

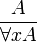
Правила вывода

М = < Т, Р, А, F >

s Каждое правило вывода имеет структуру вида:

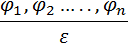
означающую, что если выведены формулы 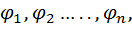называемые посылками,

то выводима также формула 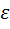, называемаязаключением

s Правила вывода логики первого порядка

§ Modus ponens (дословно ≪правило вывода≫):

Если A и A→B выводимые формулы, то B также выводима

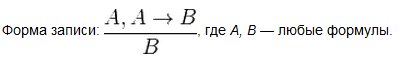
Логика первого порядка обладает рядом полезных свойств, которые делают ее очень привлекательной в качестве основного инструмента формализации математики. Главными из них являются полнота (это означает, что для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием). Логика первого порядка обладает свойством компактности: если некоторое множество формул не выполнимо, то невыполнимо также некоторое его конечное подмножество.