Основные законы булевой алгебры

Булевой алгеброй называется алгебра, в которой над логическими переменными определены три операции:

· отрицание (обозначается НЕ (NOT), черта над переменной (например, 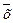), символ «Ø»);

· логическое умножение (конъюнкция) (обозначается И (AND), &, ·);

· логическое сложение (дизъюнкция) (обозначается ИЛИ (OR), Ú, +).

Для представления любой логической функции в виде формулы используются:

· символы основных операций отрицания, конъюнкции и дизъюнкции;

· буквы типа х, у, z, ... для обозначения переменных (включая буквы с индексами);

· константы 0 и 1;

· пара символов ( ), которые называются скобками.

Формулы булевой алгебры представляются конечными последовательностями символов, записанных в виде строчек и удовлетворяющих требованиям определения формулы.

Формулами булевой алгебры являются:

· булевы переменные х, у, z, ...;

· константы 0 и 1;

· выражения вида (АВ), (AÚB), 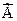, где А и В являются формулами.

В булевой алгебре при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее — конъюнкции, а затем — дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий: в первую очередь должны выполняться операции внутри скобок.

Две формулы булевой алгебры называются эквивалентными (равными, равносильными), если равны сопоставляемые им функции, т.е. принимают одинаковые значения на всех наборах значений аргументов.

Основные законы булевой алгебры, позволяющие производить различные тождественные преобразования формул булевой алгебры приведены в табл. 4.

Таблица 4