Логические операции над высказываниями. Математическая логика
Математическая логика
и
Теория алгоритмов
Методические указания
к выполнению практических работ
Омск
Издательство ОмГТУ
Составитель Л. А. Денисова, канд. техн. наук,
доц. кафедры «Автоматизированные системы
обработки информации и управления»
Данные методические указания предназначены для обеспечения практических занятий по дисциплине «Математическая логика и теория алгоритмов» и предлагаются в качестве установочных рекомендаций студентам, использующим дистанционные технологии обучения.
Приведены материалы по основным разделам математической логики и теории алгоритмов, необходимые для освоения общепрофессиональных и специальных дисциплин студентами направления подготовки 23010062 – «Информатика и вычислительная техника».
Изложены краткие сведения по основам логики высказываний, логики предикатов, формальных аксиоматических теорий и теории алгоритмов. Рассмотрены типовые примеры и приведены указания к выполнению практических работ, даны индивидуальные задания для самостоятельной работы по вариантам.
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
© ГОУ ВПО «Омский государственный технический университет», 2009
| |
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 4
ТЕМА 1. ЛОГИКА ВЫСКАЗЫВАНИЙ.. 4
1.1. Логические операции над высказываниями. 4
1.2. Формулы логики высказываний. Следование и равносильность формул. 5
1.3. Отыскание нормальных форм формул логики высказываний. 7
1.4. Тождественно истинные и тождественно ложные формулы. Проблема разрешимости. 10
1.5.Формализация рассуждений. Правильные рассуждения. 11
1.6. Задания. 12
Варианты индивидуальных заданий. 12
ТЕМА 2. ЛОГИКА ПРЕДИКАТОВ.. 15
2.1. Определение предиката. Кванторы. Формулы логики предикатов. 15
2.2. Приведенные и предваренные нормальные формулы.. 18
2.3. Выражение суждения в виде формулы логики предикатов. 19
2.4. Задания. 20
ТЕМА 3. ФОРМАЛЬНЫЕ АКСИОМАТИЧЕСКИЕ ТЕОРИИ.. 22
3.1. Построение формализованного исчисления высказываний. 22
3.2. Автоматическое доказательство теорем. Метод резолюций. 25
3.3. Задания. 27
ТЕМА 4. НЕЧЕТКАЯ ЛОГИКА.. 30
4.1. Основные понятия нечетких множеств. 30
4.2. Элементы нечеткой логики. 31
4.3. Задания. 33
ТЕМА 5. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ.. 33
5.1. Понятие алгоритма. 33
5.2. Машина Тьюринга. 34
5.3 Задания. 37
Список литературы.. 38
ВВЕДЕНИЕ
Математическая логика, как и теория алгоритмов, возникла в связи с внутренними проблемами математики, с изучением границ применимости ее теорий и методов. В настоящее время эти взаимосвязанные между собой теории получили развитие в так называемой компьютерной математике (computer science). Вот некоторые направления их использования в прикладных областях:
– при проектировании элементной базы компьютеров используется математический аппарат логики высказываний;
– в основе алгоритмических языков лежат теория алгоритмов, теория формальных систем, логика предикатов;
– тестирование программ основано на логическом анализе их структуры;
– доказательство корректности программ базируется на теории логического вывода;
– в экспертных системах используются формально-логические выводы для имитации деятельности экспертов;
– автоматизация доказательства теорем основана на методе резолюций, изучаемом в курсе логики.
Тема 1. ЛОГИКА ВЫСКАЗЫВАНИЙ
Логические операции над высказываниями
Высказыванием называется предложение, представляющее собой такое утверждение, относительно которого можно судить, истинно оно или ложно. Высказывание не может быть одновременно истинным и ложным.
По совокупности всех высказываний определяется функция истинности, принимающая значения в двухэлементном множестве {0, 1}:
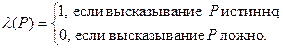
Значение l(P) называется значением истинности высказывания P.
Символ λ обычно опускают. Это связанно с тем, что в алгебре высказываний полностью отвлекаются от содержания высказываний, а изучают их только в связи с их свойством быть истинными или ложными. Поэтому каждое ложное высказывание можно рассматривать как элемент 0, а истинное – как элемент 1 и писать вместо λ(Р) = 0 или λ(Р) = 1 только Р = 0 или Р = 1.
Над высказываниями определяются следующие основные операции (логические связки), которые позволяют из имеющихся операций строить новые:
1) отрицание ØP (читается "не P");
2) конъюнкция PÙQ или P&Q (читается "P и Q");
3) дизъюнкция PÚQ (читается "P или Q");
4) импликация P®Q (читается "если P, то Q" или "из P следует Q" );
5) эквивалентность P«Q (читается "P равносильно Q" или "P тогда и только тогда, когда Q").
Операция отрицания определяется следующим образом: если P истинно, то ØP ложно и наоборот. Остальные операции определяются по таблице 1 (таблице истинности соответствующих операций).
Таблица 1
| Операнды | Определение операции | ||||
| P | Q | PÙQ | PÚQ | P®Q | P«Q |
Следует обратить внимание, что конъюнкция PÙQ истинна тогда и только тогда, когда P и Q одновременно истинны, а в остальных случаях ложна. Конъюнкцию называют логическим произведением.
Дизъюнкция PÚQ ложна тогда и только тогда, когда P и Q одновременно ложны, а в остальных случаях истинна. Дизъюнкцию называют логической суммой.
Импликация P®Q ложна тогда и только тогда, когда P = 1, а Q = 0. Импликация играет важную роль в логике высказываний. При учете смыслового содержания высказывания (а не только значений истинности) оборот “если, то” подразумевает причинно-следственную связь. Истинность импликации означает лишь то, что если истинна посылка, то истинно и заключение. При ложной посылке заключение всегда истинно.
Эквивалентность P«Q истинна тогда и только тогда, когда значения истинности P и Q совпадают.
С помощью логических операций можно из простых высказываний строить формулы логики высказываний, представляющие составные высказывания.
1.2. Формулы логики высказываний.
Следование и равносильность формул
Пропозициональными переменными называются такие переменные, вместо которых можно подставлять конкретные высказывания.
Понятие формулы логики высказываний определяется следующим (индуктивным) образом:
1) всякая пропозициональная переменная есть формула;
2) если F1 и F2 – формулы, то выражения ØF, (F1ÙF2), (F1ÚF2), (F1®F2), (F1«F2) тоже являются формулами;
3) других формул, кроме построенных по правилам двух предыдущих пунктов, нет.
Обычно внешние скобки у формулы не пишут. Подформулой формулы называется всякая ее часть, которая сама является формулой.
Если F(X1, X2,…, Xn) – формула алгебры высказываний, содержащая пропозициональные переменные X1, X2,…, Xn, и A1, A2,…, An – некоторые конкретные высказывания, то, подставив последние в данную формулу вместо соответствующих пропозициональных переменных, получим составное высказывание F(A1, A2,…, An).
Формула F(X1, X2,…, Xn) называется выполнимой (опровержимой), если существует такой набор высказываний A1, A2,…, An, который обращает эту формулу в истинное (ложное) высказывание F(A1, A2,…, An).
Формула называется тождественно истинной, или тавтологией (тождественно ложной, или противоречием), если она обращается в истинное (ложное) высказывание при всех наборах значений переменных. Обозначение тавтологии: ⊨F(X1, X2,…, Xn).
Некоторые тавтологии играют большую роль в логике и поэтому называются законами: законы рефлексивности P«P,исключенного третьего PÚP, закон отрицания противоречия (PÙP), закон двойного отрицания P«P, законы де-Моргана (PÙQ)«(ØPÚØQ), (PÚQ)«(ØPÙØQ) и другие.
Высказывания вместе с определенными для них операциями образуют алгебру высказываний.
На множестве формул логики высказываний можно определить семантические (смысловые) отношения следования и равносильности. Эти отношения играют важную практическую роль при упрощении логических выражений и построении корректных логических выводов.
Формула G(X1, X2,…, Xn) называется логическим следствием формул F1(X1, X2,…, Xn) , …, Fm(X1, X2,…, Xn) , если она обращается в истинное высказывание на всяком наборе значений переменных, для которых в истинное высказывание обращаются все формулы F1 , …,Fm. Это обозначается F1 , …,Fm ⊨G.
Две формулы логики высказываний называются равносильными, если на всех одинаковых наборах переменных значения этих формул совпадают. Равносильность формул F и G будем обозначать следующим образом: F º G. Для того чтобы установить равносильность формул, можно составить таблицы значений для каждой формулы и сравнить их. Для равносильных формул эти таблицы совпадают. Другой способ установления равносильности формул заключается в использовании некоторых установленных равносильностей формул логики высказываний.
Для любых формул P, Q, R справедливы следующие равносильности:
1. Коммутативность.
а) PÙQ º QÙP (для конъюнкции);
б) PÚQ º QÚP (для дизъюнкции).
2. Ассоциативность.
а) PÙ(QÙR) º (PÙR)ÙR (для конъюнкции);
б) PÚ(QÚR) º (PÚQ)ÚR (для дизъюнкции).
3. Дистрибутивность.
а) PÙ(QÚR) º (PÙQ)Ú(PÙR) (для конъюнкции относительно дизъюнкции);
б) PÚ(QÙR) º (PÚQ)Ù(PÚR) (для дизъюнкции относительно конъюнкции).
4. Закон де Моргана.
а) Ø(PÙQ) ºØPÚØQ (отрицание конъюнкции есть дизъюнкция отрицаний);
б) Ø(PÚQ) º ØPÙØQ (отрицание дизъюнкции есть конъюнкция отрицаний).
5. Идемпотентность.
а) PÙP º P (для конъюнкции);
б) PÚP º P (для дизъюнкции).
6. Поглощение.
а) PÙ(PÚQ) º P (1-й закон поглощения);
б) PÚ(PÙQ) º P (2-й закон поглощения).
7. Расщепление (склеивание).
а) (PÙQ)Ú(PÙØQ) º P (1-й закон расщепления);
б) (PÚQ) Ù (PÚØQ) º P (2-й закон расщепления).
8. Двойное отрицание.
Ø(ØP) º P.
9. Свойства констант.
а)PÙ1 º P; б) PÙ0 º 0; в)PÚ1 º 1;
г) PÚ0 º P; д) Ø0 º 1; е) Ø1 º 0.
10. Закон противоречия.
PÙØP º 0.
11. Закон исключенного третьего.
PÚØP º 1.
12. P®Q ºØPÚQ º Ø(PÙØQ).
13. P«Q º (P®Q)Ù(Q®P) º (PÙQ) Ú (ØPÙØQ) º (PÚØQ)Ù(ØPÚQ).
Каждая из перечисленных равносильностей может быть доказана с помощью таблиц значений функций, составленных для выражений, стоящих слева и справа от символа “º”.
