Примеры применения Марковского метода

2.4.4.1 Система с восстановлением с двумя состояниями. В качестве примера применения Марковского метода для определения показателей надежности рассмотрим восстанавливаемый объект (рис. 2.18), у которого поток отказов простейший (пуассоновский) с параметром потока , а распределение времени восстановления подчиняется экспоненциальному распределению с интенсивностью восстановления ( – средняя наработка между отказами, – среднее время восстановления).

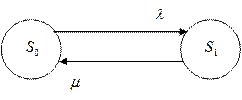
Рисунок 2.18 – Диаграмма графа состояний

Для данного примера:

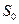- – работоспособное состояние;

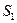- – состояние отказа;

- – вероятность работоспособного состояния при ;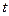

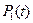- – вероятность неработоспособного состояния при .

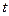Система дифференциальных уравнений для данного графа состояний имеет вид:

(2.53)

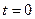
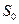Начальные условия: при , а , поскольку состояния и 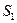представляют полную группу событий, то .

Будем решать систему уравнений относительно :

. (2.54)

Найдем решение дифференциального уравнения (2.54) при ненулевых условиях.

Тогда

, (2.55)

. (2.56)

С помощью полученных выражений (2.55) и (2.56) можно рассчитать вероятность работоспособного состояния и отказа восстанавливаемого объекта в любой момент .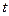

Коэффициент готовности системы 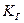определяется при установившемся режиме 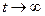, при этом , поэтому система уравнений (2.53) преобразуется в систему алгебраических уравнений с нулевыми левыми частями:

(2.54)

Решая систему уравнений (2.54) получим:

(2.55)

Параметр 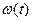потока отказов

. (2.56)

При 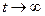(стационарный установившийся режим восстановления)

. (2.58)

Средняя наработка между отказами ( )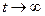

. (2.59)

Среднее время восстановления

. (2.60)

Используя выражения (2.49), (2.55), (2.59) и (2.60)

Таким образом, коэффициент готовности характеризует долю времени, в течении которого система работоспособна, а коэффициент простоя характеризует долю времени, в течении которого система ремонтируется.

Анализ изменения позволяет сделать выводы:

- при мгновенном (автоматическом) восстановлении работоспособности

- ;

- при отсутствии восстановления

- ,

т.е. вероятность работоспособного состояния объекта равна ВБР невосстанавливаемого элемента.

2.4.4.2 Система без восстановления с двумя состояниями. Метод дифференциальных уравнений может быть использован для расчета показателей надежности и невосстанавливаемых объектов (систем). В этом случае неработоспособные состояния системы являются «поглощающими» и интенсивности выхода из этих состояний исключаются. Для невосстанавливаемого объекта граф состояний имеет вид (рис. 2.19).

Рисунок 2.19 –Диаграмма графа состояний

Для данного примера:

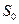- – работоспособное состояние;

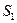- – состояние отказа («поглощающее» состояние).

Система дифференциальных уравнений для данного графа состояний имеет вид:

А вероятность безотказной работы

.

2.4.4.3 Связь структурной схемы надежности с графом состояний. Переход от структурной схемы надежности к графу состояний необходим:

1) при смене методов расчета надежности и сравнении результатов;

2) для оценки выигрыша в надежности при переходе от невосстанавливаемой системы к восстанавливаемой.

Рассмотрим типовые структурные схемы надежности (табл. 2.3). Типовые соединения рассмотрены для невосстанавливаемых систем (граф – однонаправленный, переходы характеризуются переходами интенсивности отказов 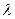). Для восстанавливаемых систем в графах состояний добавляются обратные переходы, соответствующие интенсивностям восстановлений .

Таблица 2.3 – Структурные схемы надежности и диаграммы графа состояний

Структурная схема надежности	Диаграмма графа состояний
Элементы различной надежности	Равнонадежные элементы

2.4.4.4. Система с восстановлением с множеством состояниями. Определим коэффициент готовности и коэффициент простоя системы, содержащей основной и резервных элементов, находящихся в нагруженном режиме (рис. 2.20). Отказавшие элементы образуют очередь на ремонт, который осуществляется с интенсивностью . Интенсивность отказа любого элемента равна .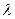

Рисунок 2.20 – Система с параллельным нагруженным резервом

Введём в рассмотрение состояния , , ,…, :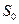

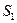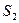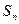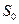- - работоспособны все 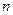элементов;

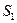- - отказал один элемент, остальные работоспособны;

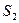- - отказали два элемента, остальные исправны;

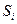- - отказали 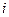элементов, остальные исправны;

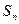- - отказала вся система, т.е. отказали все 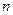элементов.

Построим граф состояний (рис. 2.21).

Рисунок 2.21 – Диаграмма графа состояний

Система дифференциальных уравнений имеет вид:

(2.61)

В установившемся режиме имеем

В результате из (2.61) получим систему алгебраических уравнений вида:

(2.61)

Из системы алгебраических уравнений (2.61) имеем:

(2.62)

Для вероятностей состояний справедливо следующее соотношение:

,

или

;

.

Из системы (2.62)

.

.