Задачи для практического занятия по логике предикатов

Эквивалентность высказываний

Законы идемпотентности:(от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):	P È P º P P Ç P º P
Закон двойного отрицания:	-(-P) º P
Законы де Моргана:	–(P È Q) º –P Ç -Q –(P Ç Q) º –P È -Q
Свойства коммутативности:	P È Q º Q È P P Ç Q º Q Ç P
Свойства ассоциативности:	P È (Q È R) º (P È Q) ÈR P Ç (Q Ç R) º (P Ç Q) ÇR
Свойства дистрибутивности:	P È (Q Ç R) º (P È Q) Ç (P È R) P Ç (Q È R) º (P Ç Q) È (P Ç R)
Закон контрапозиции:	P Þ Q º - P Þ - Q
Другие полезные свойства:	P Þ Q º - P È Q (P Þ Q) Ç (Q Þ P) º P ~ Q

Операции с логически истинными и логически ложными высказываниями:

Законы исключения констант:

P Ç T º P P È T º T

P Ç F º F P È F º P P Þ P º T

Закон противоречия: невозможно, чтобы противоречащие высказывания были одновременно истинными. P Ç –P º F

Закон исключения третьего: из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано. P È –P º T

Закон поглощения:

для логического сложения: PÈ (P Ç Q) = P;

для логического умножения: P Ç (P È Q) = P.

Преобразования формул логики предикатов

Правило переноса квантора через отрицание

Пусть а – формула, содержащая свободную переменную х. Тогда:

!("х)а(х)º ($х)!а(х)

!($ х)а(х)º ("х)!а(х)

Правило выноса квантора за скобки

Пусть а(х) содержит свободную переменную х, формула b не содержит переменной х и нет таких переменных, которые были бы связаны в одной формуле и свободны в другой. Тогда:

($ х)(а(х)Çb)º ($ х)а(х)Çb

("х)(а(х)Çb)º (" х)а(х)Çb

($ х)(а(х)Èb)º ($ х)а(х) Èb

("х)(а(х)Èb)º (" х)а(х)Èb

Если формула b содержит переменную х, то справедливы две равносильности:

($ х)(а(х)Çb(х))º ($ х)а(х)Ç($ х)b(х)

("х)(а(х)Çb(х))º (" х)а(х)Çb(" х)(х)

Правило перестановки одноименных кванторов:

("х)("у)а(х,у)º("у)("х)а(х,у)

($х)($у)а(х,у)º($у)($х)а(х,у)

Задачи для практического занятия по логике предикатов

1. Какие из следующих выражений являются предикатами:

а) «х делится на 5» (х Î N);

б) «Река х впадает в озеро Байкал» (х пробегает множество названий всевозможных рек);

в) «х² + 2х + 4» (x Î R);

г) «(х + у)² = х² + 2ху + у» (х, у Î R);

д) «х есть брат у» (х, у пробегают множество всех людей);

е) «х и у лежат по разные стороны от z» (x, у пробегают множество всех точек, a z — всех прямых одной плоскости);

ж)«ctg45°= 1»;

з) «х перпендикулярна у» (х, у пробегают множество всех прямых одной плоскости);

2. Для каждого из следующих высказываний найдите предикат (одноместный или многоместный), который обращается в данное высказывание при замене предметных переменных подходящими значениями из соответствующих областей:

а) «3 + 4 = 7»;

б) «Вера и Надежда — сестры»;

в) «Сегодня — вторник»;

г) «Город Саратов находится на берегу реки Волги»;

д) «sin 30° = 0,5»;

е) «А. С. Пушкин — великий русский поэт»;

ж) «З2 + 42 = 52»;

з) «Река Индигирка впадает в озеро Байкал»;

и) «Если число делится на 3, то оно делится на 9»;

к) «Луна есть спутник Марса»;

Построив такой предикат, постарайтесь или точно указать его область истинности, или как-то ее обрисовать.

3. Прочитайте следующие высказывания и определите, какие из них истинные, а какие ложные, считая, что все переменные пробегают множество действительных чисел:

а) ("x) ($у) (х + у = 7);

б) ($у) ("x) (х + у = 7);

в) ($х) ("y) (x + у = 7);

г) ("x) ("y) (х + у = 7);

д) [("x)( "y)(x + y = 3)]®(3 = 4);

е) ("x) [(х² > х) ~ ((х > 1) È(х < 0))];

ж) ("а) {[($х) (ах = 6)] ~ (а ≠ 0)};

з) ("b) ($а) ("x) {х² + ах + b > 0};

и) ("x) [((х > 1) È (х < 2)) ~ (х = х)];

к) ($b) ("а) ($х) (х² + ах + b = 0);

л) ($а) ("b) ($х) (х² + ах + b = 0).

4. Найдите множества истинности следующих предикатов, заданных на множестве всех точек плоскости (А, В и С — различные фиксированные точки плоскости, l — фиксированная прямая плоскости):

а) Отрезок [АВ] виден из точки X под прямым углом;

б) Точка X располагается по одну сторону с точкой А от прямой l (предполагается, что точка А не лежит на прямой l);

в) Точка X располагается на прямой l и одинаково удалена от точек Аи В;

г) Точка X симметрична с некоторой точкой отрезка [АВ] относительно точки С;

д) Точка X равноудалена от точек Аи В;

е) Точка X находится на данном расстоянии от точки В;

ж) Точка X удовлетворяет двум условиям: она одинаково удалена от точек Аи В и находится на данном расстоянии от точки С;

з) Точка X лежит на прямой между точками Аи В;

и) Точка В лежит на прямой между точками Аи X;

к) Точка X одинаково удалена от точки А и прямой l (А Îl);

л) Точка X симметрична с некоторой точкой отрезка [АВ] относительно прямой l

5. Изобразите на координатной прямой или на координатной плоскости множества истинности следующих предикатов:

а) (х> 2) Ç (х<2);

б) (х> 2) È (x<2);

в) (х> 2) ~ (x< 2);

г) (х ≥ 0) Ç (у ≤ 0);

д) (х ≥ 0) È (у≤ 0);

е) (х≥0) ® (y≤0);

ж)(|х|<3) Ç (х>2);

з) (sin х > 0) Ç (| х - 2 | < 5) Ç (lg x > 1);

и) (х² + у² > 1) ~ (ху < 0);

к) (|х|>2) ® (|x|<3);

л) (х> 2) ® (y < 2);

м) (х ≥ 0) ~ (у ≤ 0).

6. Выясните, равносильны ли следующие предикаты, если их рассматривать над множеством действительных чисел R, над множеством рациональных чисел Q, над множеством целых чисел Z и над множеством натуральных чисел N:

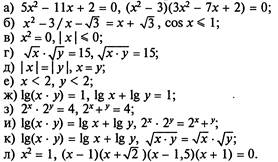
7. Введя подходящие одноместные предикаты на соответствующих областях, переведите следующие высказывания на язык логики предикатов:

а. Все рациональные числа действительные;

б. Ни одно рациональное число не является действительным;

в. Некоторые рациональные числа действительные;

г. Некоторые рациональные числа не являются действительными.

д. Всякое натуральное число, делящееся на 12, делится на 2, 4 и 6;

е. Жители Швейцарии обязательно владеют или французским, или итальянским, или немецким языком;

ж. Функция, непрерывная на отрезке [0, 1], сохраняет знак или принимает нулевое значение;

з. Некоторые змеи ядовиты;

и. Все собаки обладают хорошим обонянием;

к. Все ромбы являются параллелограммами;

л. Некоторые параллелограммы являются ромбами;

м. Ни один параллелограмм не является ромбом;

н. Некоторые ромбы не являются параллелограммами;

о. Ни один ромб не является параллелограммом;

п. Все параллелограммы являются ромбами.

Задачи для практического занятия на тему «правильные и неправильные рассуждения»

Проанализируйте следующие рассуждения на предмет их правильности. Для этого выявите логические схемы, на которых они основаны, и выясните, справедливы ли они.