Таблицы истинности логических функций двух аргументов
| Аргу-мен- ты | Логические функции | ||||||||||||||||
| А | В | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 |
Исходя из значений логических функций F1…F16 в таблице истинности, можно эти функции синтезировать.
 |  |
1. F1 = А * А = В * В
Равносильные логические выражения.Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак « = ».
Таблица истинности F1
| А | В |  А А |  В В | F1 |
2. F2 = A * B
Таблица истинности F1
| А | В | А * B |
 3. F3 = A * B
3. F3 = A * B
Таблица истинности F3
| А | В |  B B |  A * В A * В |
4. F4 = A
Таблица истинности F4
| А | В | F4 = A |

5. F5 = B * A
Таблица истинности F5
| А | В |  A A |  B * A B * A |
6. F6 = B
Таблица истинности F6
| А | В | F6 = B |
 |  |
7. F7 = (A * В ) v (B * A)
Таблица истинности F7
| А | В |  A A |  В В |  А * В А * В |  B * A B * A |   (А * В ) v ( B * A ) (А * В ) v ( B * A ) |
8.
8. F8 = A v B
Таблица истинности F8
| А | В | Av B |
 |
9. F9 = A v B
Таблица истинности F9
| А | В | Av B |  Av B Av B |
 | ||||||
 |  | |||||
 |
10. F10 = (А * В ) v ( B * A ) F10 = F7
Таблица истинности F10
| А | В |  A A |  В В |  А * В А * В |  B * A B * A |   (А * В ) v ( B * A ) (А * В ) v ( B * A ) |    (А * В ) v ( B * A ) (А * В ) v ( B * A ) |
Логическое равенство (эквивалентность).Составное высказывание, обозначенное с помощью логической операции эквивалентностиистинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны, обозначается « А – В ».Исходя из этого,можно сказать,что F10 является функцией эквивалентности и запишется так: F10 = A - B, а её таблица истинности будет иметь следующий вид:
Таблица истинности логической функции эквивалентности
| А | В | А - В |
11.  F11 = B
F11 = B
Таблица истинности F11
| А | В |  В В |

 12. F12 = F5 =B * A
12. F12 = F5 =B * A
Таблица истинности F12
| А | В |  A A |  B * A B * A |   B * A B * A |
 |  |
13. F13 = F4 = A
Таблица истинности F13
| А | В |  A A |
 |
14. 
 F14 = F3 = A * B
F14 = F3 = A * B
Таблица истинности F14
| А | В |  B B |  A * В A * В |   A * В A * В |
В обыденной и научной речи кроме базовых логических связок « И», «ИЛИ», «НЕ» используются и некоторые другие: «ЕСЛИ…, ТО», «…ТОГДА И ТОЛЬКО ТОГДА, КОГДА…» и другие. Некоторые из них имеют своё название и свой символ, и им соответствуют определённые логические функции.
Логическое следование (импликация).Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «ЕСЛИ…, ТО…».
 Логическая операция импликация «если А, то В», обозначается А В и выражается с помощью логической функции F14, которая задаётся соответствующей таблицей истинности.
Логическая операция импликация «если А, то В», обозначается А В и выражается с помощью логической функции F14, которая задаётся соответствующей таблицей истинности.
Таблица истинности логической функции импликация
| А | В | 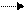 А В А В |
Составное высказывание, образованное с помощью операции логического следования (импликация) ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
 |
15. F15 = A * B
Таблица истинности F15
| А | В | A * B |  A * В A * В |



 16. F16 = A * A = B * B
16. F16 = A * A = B * B
Таблица истинности F16
| А | В |  A A |  A * A A * A |   A * A A * A |
